k近邻(KNN)复习总结

摘要：

　　1.算法概述

　　2.算法推导

　　3.算法特性及优缺点

　　4.注意事项

　　5.实现和具体例子

　　6.适用场合
内容：

1.算法概述

　　K近邻算法是一种基本分类和回归方法；分类时，根据其K个最近邻的训练实例的类别，通过多数表决等方式进行预测；k近邻法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的"模型"（Cover和Hart 在1968）--参考自《统计学习方法》

　　回归是根据k个最近邻预测值计算的平均值--参考自scikit-learn官网

2.算法推导

2.1 kNN三要素

　　k值的选择：当k值较小时，预测结果对近邻的实例点非常敏感，容易发生过拟合；如果k值过大模型会倾向大类，容易欠拟合；通常k是不大于20的整数（参考《机器学习实战》）

　　距离度量：不同距离度量所确定的最近邻点是不同的

　　分类决策规则：多数表决（majority voting）规则是在损失函数是0-1损失函数时的经验风险最小化

2.2 KD树：解决对k近邻进行快速搜索的一种二叉树，构造kd树相当于不断用垂直于坐标轴的超平面对特征空间进行划分，最终构成一系列的K维超矩阵区域；每一个节点对应于一个k维超矩形区域。一般情况下顺序选择坐标轴及坐标轴的中位数（下图中取的最中间两个数较大的一个数）进行切分。kd树是平衡的但效率未必最优--参考自《统计学习方法》

      KD树只在小于等于20维的数据集上可以快速搜索，但是当维数增长时效率降低　　

      如下图对T = {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}建立kd树的结果：

　　

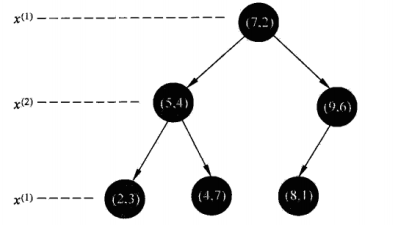
2.3　ball tree:解决高维空间下kd树失效的一种树形结构；Ball树根据质心C和半径r对数据进行递归的划分，每一个数据点都会被划分到一个特定的质心C和半径r的的超球体里面，在搜索的时候，候选的点会使用|x+y| <= |x| + |y|进行筛选（papers:“Five balltree construction algorithms”） 

　　如下图是显示了一个2维平面包含16个观测实例的图（参考自）：

　　

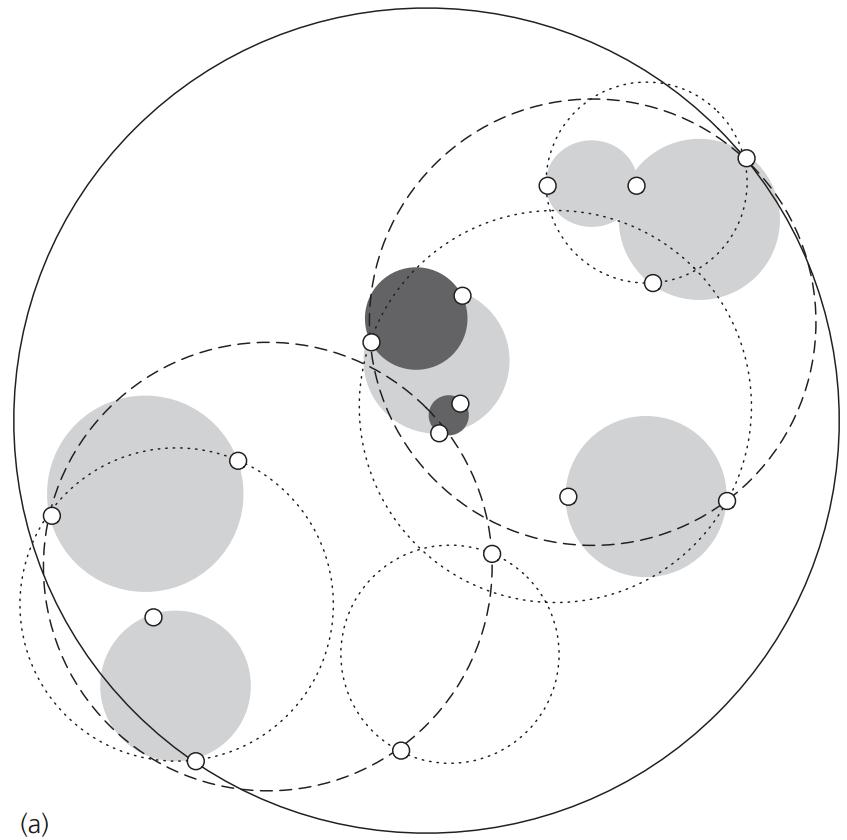
3.算法特性及优缺点

　　优点：精度高，对异常值不敏感

　　缺点：k值敏感，空间复杂度高（需要保存全部数据）,时间复杂度高（平均O(logM)，M是训练集样本数）

4.注意事项

　　归一化：基于距离的函数，要进行归一化；否则可能造成距离计算失效

5.实现和具体例子

　　构建KD树并使用KD树进行最近邻搜索（《统计学习方法》算法3.2和3.3）

　　机器学习实战中的提高约会网站配对指数和手写识别的例子（numpy实现，未使用KD树）

　　scikit-learn使用KNN进行分类的例子（分类决策上可以加大邻近点的权重)；

　　ball tree 实现的例子（有时间研究下）

6.适用场合

　　是否支持大规模数据：单机下时间和空间消耗大，不过可以通过分布式解决（github上找到的一个spark knn实现，有时间研究下）

　　特征维度

　　是否有 Online 算法:有

　　特征处理：支持数值型数据，类别型类型需要进行0-1编码