【黑金原创教程】【TimeQuest】【第五章】网表质量与外部模型
声明：本文为黑金动力社区（http://www.heijin.org）原创教程，如需转载请注明出处，谢谢！
黑金动力社区2013年原创教程连载计划：
http://www.cnblogs.com/alinx/p/3362790.html
《FPGA那些事儿--TimeQuest 静态时序分析》REV5.0 PDF下载地址：
http://www.heijin.org/forum.php?mod=viewthread&tid=22811&extra=page%3D1
第五章：网表质量与外部模型
5.1 网表质量的概念
5.2 Fmax评估值
5.3 外部模型①
5.4 外部模型②
5.5 推导外包资料的公式
5.6 外部模型的input/ouput 约束指令
总结：
第五章：网表质量与外部模型
5.1 网表质量的概念
笔者在第二章稍微谈过网表 ... 不过现在又为何会无缘无故提及它呢？笔者以前曾以为TimeQuest 等静态时序工具是按照实际的物理情况来评估物理时序，不过事实却不是如此。即使静态时序工具再怎么神，身为数学工具的它只能模拟出“近似”的情况而已，其中一定留有余量。
同样，笔者也在第四章不停重复“默认网表下 ... 默认网表下”... 难道读者不觉得有伏笔吗？笔者不是在卖关子，因为根据笔者的脚步而言，要理解接下来的内容，必须对TimeQuest 做好足够的认识。为此，笔者特地绕了一个大圈，为了就是让同学们做好准备。
TimeQuest 作为数学工具必须根据各种 CASE 作出分析，CASE 简称点就是环境或者状况，然而 TimeQuest 却有两种CASE，其一是 Worst Case，其二是 Best Case ，前者对应 slow model，后者对应 fast model。
表5.1 Worst Case 和 Best Case 的对应因数。
| Case | 模型 | 环境 | 温度 | 性能限制 |
| Worst Case | slow | 极端 | 低温/高温 | 高 |
| Best Case | fast | 最佳 | 室温 | 低 |
如表5.1所示，除了 slow model 和 fast model 以外，Worst Case 分别对应的其他因数有，极端环境，还有低温/高温的影响。换之 Best Case 对应有最佳环境和室温。
所谓Worst Case是指极端的环境，也指主供源的电压不稳定以外，还有各种内部延迟因数都推向极端，结果拖累整个硬模型的速度——Fmax，最终成为 slow model，如此反思于是越坏的情况，衍生的保险余量就越多，因此性能限制也很大。
所谓 Best Case是指最佳或者理想环境，也指不仅足够而且还稳定，此外各种内部延迟因数越近似实际，也愈小，结果而言整个硬模型的速度——Fmax也会跟着提高，最终成为 fast model。如此反思，越是理想的环境，一旦遇上麻烦可衍生的保险余量也有限，因此性能限制也很小。
笔者这样一讲，可能会让同学们一时之间不知所措 ... 不过我们可以这样认为。保险余量就好比一位生存者，常常会思考最坏的情况，假设情况A。换言之，只要一天不发生比情况A更糟的事情，这位生存者都可以有余过活。相反的，那些乐天的屁民们已经习惯过着舒适的生活，假设为情况B。换句话说，只要稍微发生比情况B哪怕糟一点点的事情，屁民们就会被吓到半死。
TimeQuest所谓的默认 CASE —— slow model也指最极端的情况，结果而言Time Quest
就像为世界末日作好准备的生存者，往往评估和分析极端环境的各种状况。粗略一点说
，凡是通过 slow model 分析的硬模型，fast model 理应也合格。反过来说，凡是在 fast model合格（屁民）的硬模型，不一定通过 slow model的分析。
继续深入之前，让我们回顾一下什么是 post-fit 什么是 post-map。虽然官方的手册上有定义，用俗话说的话，post-fit 网表会参考近似物理的参数（优化之后），而 post-map 只会参考原生的编译结果（优化之前）。论质量而言，post-fit 比起 post-map 更适合。
所谓的默认网表，是指 post-fit model -slow ,也是双击 Create Netlist 快捷选项会产生的结果，对应的tcl命令式create_timing_netlist -model slow。结果而言 TimeQuest 是不择不扣的生存主义者，打从一开始就已经评估任何最坏的情况。当然读者也可以回忆一下在第三章中所描述的“玩具与金钱还有妈妈”的比喻。
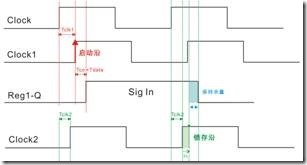
这个章节的重点，我们仅要了解各种 case 对内部延迟因数造成的影响，其中也包括寄存器的特性，如tsu，tco和th等。笔者继续以实验三的 delay_monster 为例子，其中除了100Mhz的 create clock 声明以外，一切约束命令通通都拿掉。
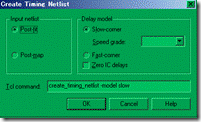
图5.1.1 默认网表 worst case / slow model
首先我们先示范默认网表，亦即 worst case 或者 slow model，读者可双击 create timing
netlist 选项，也可以调出 Create Timing Netlist 窗口，然后手动建立（如图5.1.1所示）
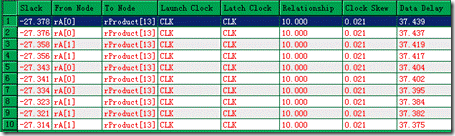
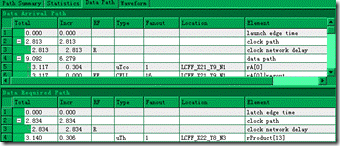
图5.1.2 随意举例10个节点的setup报告。
让后随意列出10个节点的 setup 报告，目前该时序违规与否，不是我们要关心的问题。
然而重点就在于 slack 和Data Delay值，以节点1为例 -27.378ns 和 37.439ns。
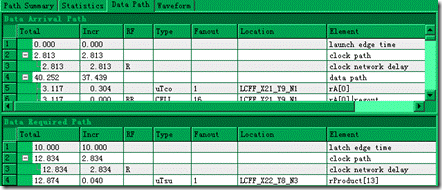
图5.1.3节点1的详细信息（Setup）。
然后打开节点1的详细信息，在此观测 clock path—2.813ns 还有 uTco—0.304ns 和 uTsu—0.040ns。
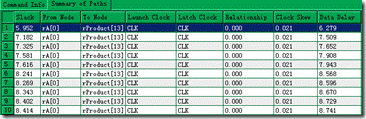
图5.1.4 随意举例10个节点的hold报告。
再来随意举例10个节点的hold 报告，以节点1为例，slack 为 5.952ns，而Data Delay 为6.279ns。
图5.1.5 节点1的详细信息（Hold）。
再来展开节点1的详细信息和观察 uTh—0.306ns。
图5.1.6 Fmax结果。
接着双击 Report Fmax Summary 调出 Fmax 简报，结果如图5.1.6所示—26.75Mhz。
===================================================================
图5.1.7 自定义网表 best case / fast model
在此让我们建立 best case 网表，亦即 fast model。这个必须手动建立，如图5.1.7 所示。
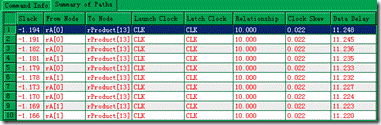
图5.1.8 随意举例10个节点的setup报告。
接着随意列举10个节点的setup报告，同样 ... 此时时序违规与否都不是重点，让我们注意节点1的 slack—1.194ns 还有 Data Delay—11.248ns
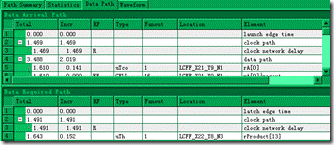
图5.1.9节点1的详细信息（Setup）。
再来展开节点1的详细信息，关注 clock path—1.469ns，uTco—0.141ns和uTsu—0.032。
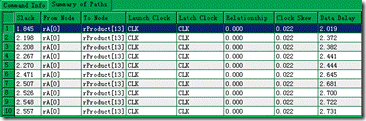
图5.1.10 随意举例10个节点的hold报告。
同样随意举例10个节点的hold时序报告，关注节点1的 slack—1.845ns。
图5.1.11 节点1的详细信息（Hold）。
接下来展开节点1的详细信息，关注 uTh—0.152ns。
图5.1.12 Fmax结果。
最后取得 Fmax 简报 —— 89.33Mhz
===================================================================
根据上述的内容，笔者以节点1为例（Setup和Hold各不同），然后根据不同的网表状况，再取各种参数做出表5.1。
表5.1 节点rA[0]~rProduct[13] 革命剧Worst Case 和 Best Case的相关参数比较。
| rA[0]~rProduct[13] | worst case/ slow model | best case/ fast model |
| Setup Slack | -27.378ns | -1.194ns |
| Data Delay | 37.439ns | 11.248ns |
| Clock Path | 2.813ns | 1.469ns |
| uTco | 0.304ns | 0.141ns |
| uTsu | 0.040ns | 0.032ns |
| Hold Slack | 5.952ns | 1.845ns |
| uTh | 0.306ns | 0.152ns |
| Fmax（约束前） | 26.75Mhz | 89.33Mhz |
| Fmax（约束后） | 107.01 MHz | 357.27 MHz |
实际上表5.1不用看都知道那是一面倒的情形，亦即节点 rA[0]~rProduct[13] 的worst case 相较 best case 之下都呈现各种极端的参数结果。由于 worst case 把所有内部延迟因数都推向极端，结果导致 Fmax 的速度下降（无论是约束前或者约束后）。不过表5.1还有一个特殊的情形让同学们在不知觉中产生疑问 ...
“worst case 的 hold slack 不应该比 best case 的 hold slack 更小才对吗？”，让我们回忆一下用屁股求出 hold 余量的公式：
保持余量 = 数据抵达时间 - 数据获取时间
Hold Slack = Data Arrival Time - Data Required Time
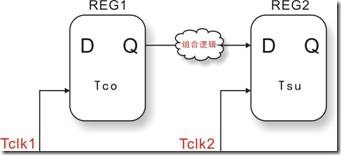
数据抵达时间 Data Arrival Time = 启动沿 + Tclk1 + Tco + Tdata
数据获取时间 Data Required Time = 锁存沿 + Tclk2 + Th
= 理想保持关系值 + Tclk2 + Th
Hold Slack 是 Data Arrival Time 相减 Data Required Time 以后的结果，其中最为关键的是 Tdata（Data Delay），worst case 与 best case 相比之下 worst case 的 Data Delay还有大过 best case 的 Data Delay。结果也因此造成 worst case 的 hold 余量大于 best case 的 hold余量。
===================================================================
笔者曾经这样思考过：“创建网表会不会也是某种约束呢？”例如创建默认网表A，sdc文件下就会添加相关的约束，然后编译器会依照这个约束命令来创建网表A的硬模型
；如果是网表B，就会创建网表B的硬模型等 ... 这是学习 TimeQuest的思路陷阱。
事实上，网表的概念非常直接 ... 首先把TimeQuest 想象成硬模型的模拟器，我们可以假设 best case 硬模型是最接近物理硬模型，不过相较实际的硬模型 best case 的硬模型还保留10~20%的余量。假设物理硬模型的某个延迟值是10ns，那么best case硬模型对于10ns采取保留的12ns。
相反之下 worst case 硬模型是最保险的硬模型，比起 best case 硬模型worst case 硬模型相较物理硬模型有80~90%的余量。再假设物理硬模型的某个延迟值是10ns，那么worst case硬模型会采取保险的 19ns。
这个作法有一个好处 ... 就算 best case 硬模型遇见状况，如果不超过10~20%的余量范围，结果还是健康。相反对于 worst case 硬模型而言，余量范围比起 best case 硬模型还要更大。举例某个状况是发生35% 的范围，那么best case 硬模型就会出现问题，换之 worst case 硬模型还是稳如泰山。
让我们继续思考 ... 有关延迟怪兽实验的重点就是“即时式Booth乘法器”。31ns的延迟压力是不是实值呢？31ns延迟压力是 worst case硬模型的保险估算，最接近是实值是 best case硬模型，延迟压力大约是10ns左右。即时式 Booth 乘法器的压力取值实际上比best case硬模型还要低，不过具体的数值是多少呢？这点我们就不知道了。
实验六的 delay_master 笔者以 worst case 硬模型评估即时式 booth 乘法器的延迟压力，大约是30ns左右，然后供源和加工时间都给予40ns的。
总体而言，默认下的TimeQuest都是采取保险措施，亦即默认下网表是 slow model，默认硬模型是 worst case。不过，这不是强制性的 ... 同学们还有各种选项自由选择，如post-fit和post-map，或者 speed grade，还是 zero ic delay 等。
不过根据一般使用习惯，有时候需要比 worst case 更极端的环境 ... 假设同学预测到在环境A会使时钟频率更动10%，除了选择 worst case 硬模型以外，同学还可能不放心，所以在 create clock（声明主时钟）的时候，会故意为主时钟留下10~20%的余量 ... 如100Mhz的频率，会用80~90Mhz或者100~120 Mhz的频率分别测试 worst case 硬模型。
另外还有一种说法说，best case网表 setup分析不容易合格，worst case 网表 hold分析不容易合格。结果会分别用 best case 针对 setup分析，用 worst case 针对 hold 分析，如果best case下 setup分析有余量 & worst case 下 hold 分析有余量，那么这个模块就是没问题。
此外也有这样的说法，在室温（常温）以外的极端温度：如在低温状态，所有资源会有所迟钝；高温状态会提高资源的阻值。所以 worst case 有时候也用来测试模块在某种恶劣的温度下是否能正常工作。
嘛 ... 网表的故事是千奇百怪的，对于普通的使用而言： worst case 最保险但是性能限制大；best case 保险有限但是性能限制小。说白一点，假设FPGA的最高频率是300Mhz，如果使用 best case，最高频率使用允许是280Mhz左右；如果使用 worst case，最高频率的使用允许是60Mhz左右。
总结说“牛排到底要几成熟最后还是要根据客官当时的口味”，笔者是非常怕死，所以吃牛排都是全熟，亦即 worst case 最适合笔者 ... 结果同学又如何呢？最后补上不相关的话题 ... 当TimeQuest为某个设计建立网表（硬模型）的时候，而这个网表只是分析对象却没有环境因数，或者缺少分析环境 ... 因为如此，我们需要透过各种约束命令为分析对象制造刺激，以致达到接近的现实的环境因数，这也是俗称的网表约束。
这个环境因数就是所谓的内部延迟因数，还有外部延迟因数。内部延迟因数TimeQuest可以自动晓得，反之外部延迟因数却必须人为告知。假设某个设计的硬模型，它的外部路径有3ns的延迟 ... 当我们用TimeQuest这个硬模型的时候，我们有必要将3ns延迟的外部路径告诉TimeQuest，好让它可以分析3ns的延迟是否对这个硬模型的时序作出违规。
5.2 Fmax评估值
fmax 是什么？Fmax 是一个用处不大的评估值，亦即某节点的最高频率（也可以理解成是组合逻辑的数量），同时也是网表性能限制的评估值。当我们双击 Report Fmax Summary，TimeQuest 会将某个节点的 Fmax 提出；如果某个设计有时序违规，TimeQuest 又会将那个有问题的 Fmax 提出。
Fmax之所以暧昧是因为它仅评估某个节点 ... 不，更贴切说是部分节点的最高频率。在一群小朋友之中有几位是特别调皮，结果我们却不能说所有小朋友都一样调皮，Fmax的情形就好比这个比喻。在前面我们了解过 worst case 是某个极端的状况，亦即余量范围的保留很大，内部延迟压力的保险取值也随之很高，结果却导致Fmax的评估降低。换句话说，best case 的 Fmax评估比起 worst case 有更好的表现（也更接近实体的Fmax评估）。
图5.2.1 Fmax评估模型。
fMAX = 1/(<register to register delay> - <clock skew delay> + <micro setup delay> + <micro clock to output delay>)
clock skew delay = <clock to destination register delay> - <clock to source register delay>
= Tclk2 - Tclk1
图5.2.1 是Fmax评估模型（基本上也是基于 TimeQuest分析模型）而Fmax求出的公式如上述所示，包含：reg2reg delay 就是两者寄存器之间的总和延迟，亦包括组合逻辑延迟，路径延迟等；clock skew delay，中文叫时钟差也是 Tclk2 相减 Tclk1的结果；micro setup delay 的符号是 Tsu，也是目的寄存器最小的建立时间；micro clock to output
delay 的符号是 Tco，也是源寄存器输出最小延迟时间。
从一个简单的公式中我们可以理解到，Fmax事实上是单个节点的最高频率评估值，其中最左右 Fmax 的凶手就是 reg2reg delay ... 粗略点说，Fmax高低是否，是由寄存器之间夹着的组合逻辑的延迟压力来决定。Fmax之所以暧昧是因为TimeQuest每当给出 Fmax，实际上是针对“最差劲节点”的评估值。
换句话说，如果某个设计出现时序违规，TimeQuest就会给出那个“最差劲节点”的Fmax，而不是其他 ... 那怕其它节点也是违规，只要不是最差劲就不会被TimeQuest提名。
“如何提升Fmax”算是学习TimeQuest的迷信吧 ... 有许多同学认为只要Fmax比系统时钟（主时钟）的频率还要高时序越Okay。话说这种迷信也不无道理，因为 Fmax是针对“最差劲节点”... 换言之，如果该“最差劲节点”得到好成绩，那些不是最差劲的节点的成绩当然比“最差劲节点”好。这回就让笔者暂时入乡随俗和大伙一起迷信，一同寻找“提升Fmax”的升仙之路。
Fmax另一种既是“组合逻辑的数量”，如何减少组合逻辑的数量，直接上与 HDL的建模有十足的关系，不过我们先抛开 HDL不说 ... 如此一来，网表的质量就是下一个因数，同样我们也抛开网表不说 ... 这个抛开，那个抛开，余下还有什么因素可以影响Fmax呢？啊 ... 就只剩下编译器了。
我们知道软模型要变成硬模型就需要经过编译器的综合 ... 话是那么说，不过我们又要如何设置编译器呢？回去Quartus，Assignment菜单进入 Setting :
图5.2.2 Physical Synthesis Optimizations 优化选项。
如图5.2.2所示，我们可以打开相关的选项如 Perform register retiming；Effort Level - Extra；Perform register duplication。
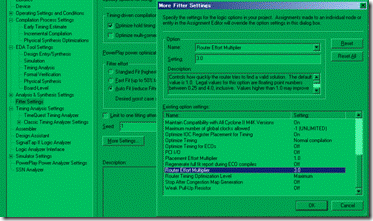
图5.2.3 Filter Settings 优化选项。
或者进入 Filter Setting，打开 More Setttings，然后将 Router Effort Multiplier 设置3.0 还有 Router Timing Optimization level 设置 Maximum。基本上设置上述优化选项以后，Fmax可以提高 10~15%，不过要增加编译的时间。（至于这些优化选项有什么具体的意义？请高抬贵手放过笔者，自己回去翻翻Quartus手册就可以知道了）
好了，让我们把主题切回 Verilog ... 虽然说减少组合逻辑就等于提升 Fmax，不过在建模的时候，使用组合逻辑是不可避免的，而且组合逻辑的使用数量我们也是模糊。举个例子来说：
if( C1 == 10 ) begin ... end
当我们声明 if，不知使用了N个组合逻辑 ... 然后声明 == 有不知道使用了N个组合逻辑。说实在，如果不使用 if 或者 == 等这些关键字HDL 就不是 HDL了。既然如此 ... HDL 与 Fmax 之间还存在什么“优化空间”呢？我们又该如何下手呢？同学们还记得《整合篇》里出现过的“操作模式”吗？事实上，我们可以从操作模式上下手，不过这话又如何说呢？
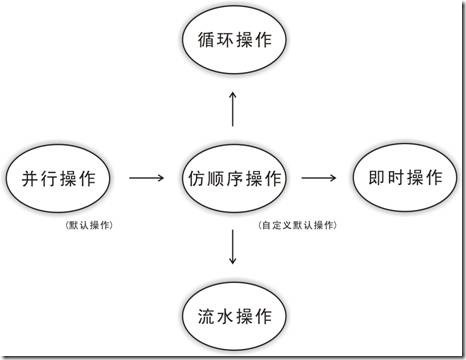
图5.2.4 笔者所知的各种操作模式。
HDL有并行操作的本质，并行操作自然而然也是HDL的默认操作，可是这种默认操作就像没有容器的水源，不好控制。结果笔者就自定属于自己的义默认操作，亦即仿顺序操作了 ... 并行操作如果要模仿顺序操作，根本上就要付出最基本数量的组合逻辑，建立可以支持顺序操作的结构。
据笔者所知，仿顺序操作可以转换成为其他操作模式 ... 如循环操作，它本质上还是顺序性的操作模式，不过它重复利用同一个资源，结果而言会比方顺序操作少用一点资源；即时操作就不用说了，本身就是一个大组合逻辑，也是Fmax最大的敌人；至于流水操作是最接近并行操作的操作模式，它不像仿顺序操作那样用而外的资源建立支持顺序的结构，结果而言它拥有的Fmax 比其它操作模式高。
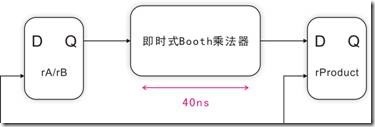
图5.2.4 即时操作。
如果不苟其他小节，让笔者举个简单的例子，如图5.2.4所示，夹在两个寄存器之间是即时式Booth乘法器。换言之两个寄存器之前存有一个40ns延迟压力的组合逻辑，不过过大的延迟压力会降低 Fmax，因此我们必须更改 Booth 乘法器的操作模式，其中流水操作是最为理想。
图5.2.5 流水操作。
同样继续不苟其他小节的话 ... 笔者将即时式Booth 乘法器随便分尸成8个部分，因此40ns的延迟压力就会被品均化为5ns，延迟压力的降低随之也会提升 Fmax。上述只是粗略的例子而已，虽说流水操作在 Fmax 的表现上拥有最好的成绩，不过流水操作不是什么场合也适合，如“步骤性强的操作”它就显得英雄无用武之地了。
HDL除了操作模式以外，还有HDL的使用习惯 ... 如：嵌套If的层次又或者 <= 和 = 的使用，让笔者举个简单的例子。
if( C1 == 1 ) //嵌套 if
if( C1 == 2 )
if（C1 == 3）
begin rA = 1 + Z; rB <= rA; end // 应用即时事件
嵌套if 按原理来说会建立更深的逻辑层次 ... 虽然这样的做法没有错，不过从代码的解读来讲是非常不推荐。应用即时事件是笔者的坏习惯，好处上可以偷吃时钟，坏处上增加该节点的延迟压力。总结来说 ... HDL 如何优化 Fmax归根就底还是需要根据当时的情况而定，所以是没有绝对的规则。
好了，有关 Fmax的故事就讲到这里吧 ... 同学们好好记住，Fmax不过是一个用处不大的评估值而已，虽说 Fmax 越高越好，不过不是每个设计都需要那么高的 Fmax。此外Fmax也是性能限制的另一种评估值。
5.3 外部模型①
如果笔者说：“大部分的约束命令都是为外部延迟因数而存在 ... ”，同学们又相信吗？
事实上，这句话一点也不夸张 ... 在第三章中笔者曾解释说，外部和内部之间的区别就是 TimeQuest 知道与不知道，自动与手动。直接点说，内部各种延迟因数就好比 TimeQuest身上的一块肉，它当然知道这块肉是什么样子，既然它知道这块肉是什么样子，TimeQuest自然会晓得这块肉的相关信息。这就是所谓的 知道和自动。
外部延迟因数就好比别人身上的一块肉，TimeQuest自然而然不知道这块肉的具体形状，
结果那个人就无比告诉TimeQuest自己身上的那块肉是在哪里，是什么形状等相关信息。者就是所谓的不知道与手动。因此如此，TimeQuest有大部分的约束命令就是用来告诉TimeQuest相关的“外部信息”。
在此之前，先让我们回忆一下之前学过的内容 ... TimeQuest事实上只会在模型里打滚的猪头，亦即只要它离开模型，它就不晓得如何打滚了，这个模型就是我们熟悉的TimeQuest模型。所以说，TimeQuest能不能分析外边的时序状况之前，TimeQuest模型能不能山寨？如何山寨？才是头号任务。
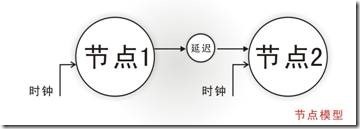
图5.3.1 节点概念的TimeQuest模型
图5.3.1是最没有个性的TimeQuest模型 ... 换句话说，节点模型是概念上的TimeQuest模型，不过除了时钟固定以外，节点1，节点2和延迟都会随着山寨的目标不同也跟着改变。
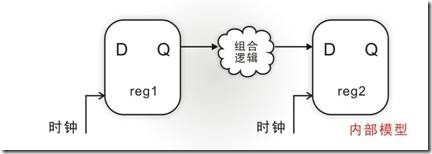
图5.3.2 内部的TimeQuest模型。
图5.3.2 是大伙再熟悉不过的内部 TimeQuest模型，同时间也是默认下的TimeQuest模型，亦即除了时钟信号不变以外，就是两个寄存器夹着一个组合逻辑。根据FPGA的基本资源而言，除了寄存器以外的一切，如乘法器，PLL等都可以看成组合逻辑。
图5.3.3 外部的TimeQuest模型。
图5.3.3是外部的TimeQuest模型（简称外部模型）也就是接下来我们要学习的内容。事实上外部模型是最麻烦，也是上镜率最低的TimeQuest模型。它之所以麻烦是因为它有fpga2ic 或者 ic2fpga之分，fpga2ic 也是fpga输出致 ic，又说ic读入fpga；换之
ic2fpga 是ic输出致ic，又说fpga读入ic。至于外部延迟有第三章所说的种种。
之所以说外部模型上镜率最低是因为外部模型的山寨成功率是非常低，除了特定的 ic 芯片如 sdram或者高速 dac/adc 等以外，外部模型几乎不能成立。话虽这么说，不过大部分约束命令却因它而生，可见它在学习中有多重的分量。
丑话说在前头，在后来的实验里，笔者也只能用 sdram 作为学习对象，那些不熟悉的同学应该好好补补一下与 sdram有关的知识 ... 老王卖瓜一定会自卖自夸，笔者建议《整合篇》的第三章，嘻嘻。那么，让我们开始吧。
===================================================================
笔者在前面说过，外部模型和内部模型之间的区分就在于知道与不知道，自动与手动。
至于是什么样的“不知道”的外部因数，必须通过“手动”告诉 TimeQuest呢？
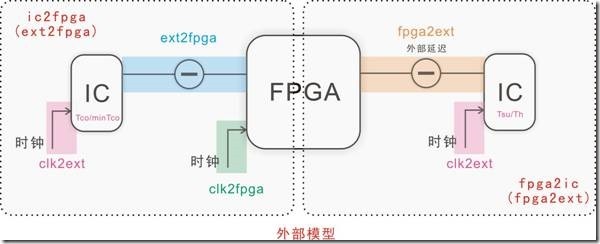
图5.3.4 各种需要告诉 TimeQuest的延迟因数。
基本上要告诉 TimeQuest的外部延迟因数不算多，在此有可以划分2个情况：
fpga2ic：
fpga2ext是fpga致ic信号的走线延迟；
clk2fpga是时钟信号致fpga的走线延迟；
clk2ext是时钟信号致fpga的走线延迟；
Tsu/Th 外部器件的寄存器特性；
（Tsu信号建立时间；Th信号保持时间）
ic2fpga：
ext2fpga是ic致fpga信号的走线延迟；
clk2fpga是时钟信号致fpga的走线延迟；
clk2ext是时钟信号致fpga的走线延迟；
Tco/minTco 外部器件的寄存器特性；
（Tco信号输出时间；minTco最小信号输出时间）
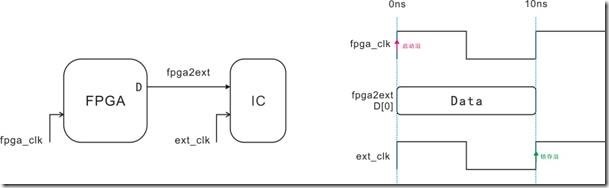
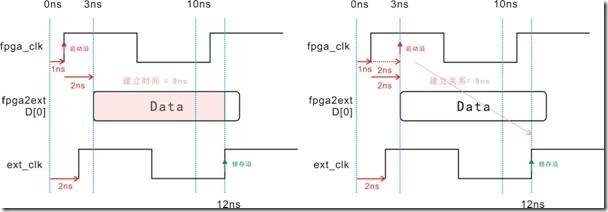
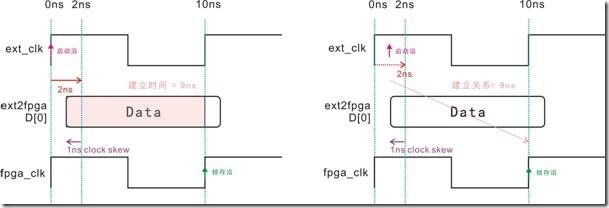
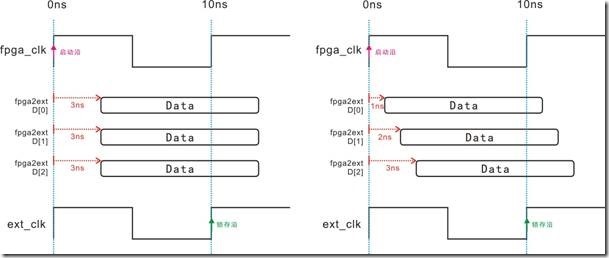
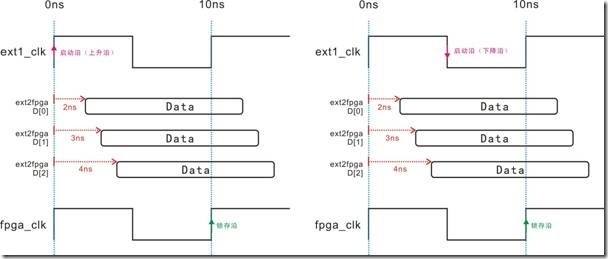
图5.3.5 （左）fpga2ic简单例子（右）理想时序图。
假设有一个简单的fpga2ic例子，如5.3.5的左图所示。fpga向ic发送一个时钟周期的D[0]，如5.3.5的右图所示，此时时序图是理想状态。
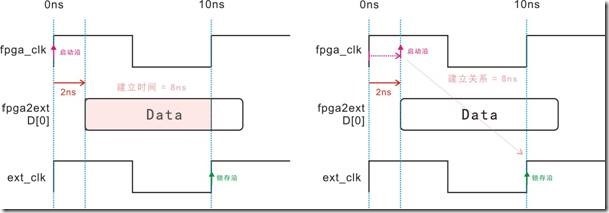
图5.3.5 建立时间与建立关系的等价图。
图5.3.5左边是信号D[0]有2ns的延迟，随之导致 Data向右移动2ns，最后Data的建立时间剩下8ns。图5.3.5右边是等价图，这个等价图基本上是无视Data。换句话说，2ns的延迟，让启动沿向右移动2ns，结果使得建立关系成为8ns。图5.3.5有一个重点，亦即左图是数据与时钟相互作用，取得数据的建立时间；相反，右图里的时钟和数据相互作用不大，而是用启动沿和锁存沿取建立关系。
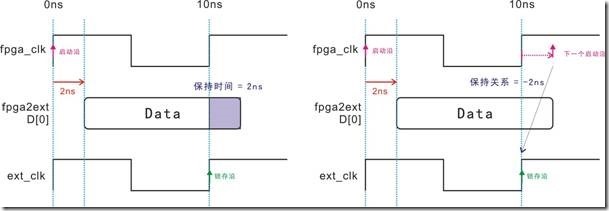
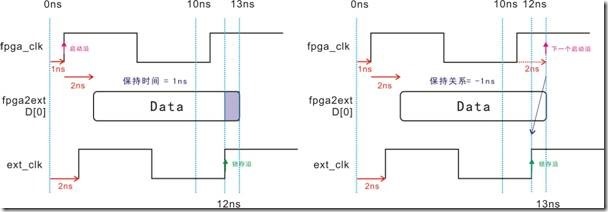
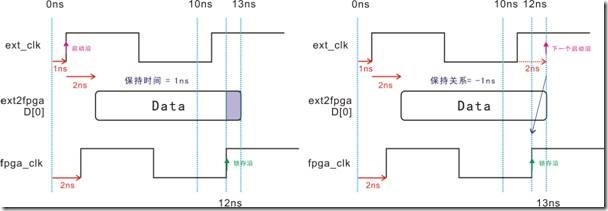
图5.3.6 保持时间与保持关系的等价图。
如果建立时间和建立关系有等价图，同样保持时间与保持关系也有等价图，如5.3.6所示。左图是 D[0] 受2ns延迟，接着数据向右推向2ns，最后取得2ns的保持时间。换之，右图是建立时间的等价图，亦即2ns延迟影响下一个启动沿向右移动2ns，结果导致建立关系取得-2ns。
建立时间或者保持时间是分析一般时序图时用来评价数据的有效性，换之建立关系和保持关系是TimeQuest应用在模型或者公式的参考值。不过不管怎么样，理想时序 ... 更贴切说是在理想状态下，建立时间或者建立关系相等于时钟周期，保持时间或者保持关系相当于零值。在此，我们先理解这些，接着再继续往后看 ...
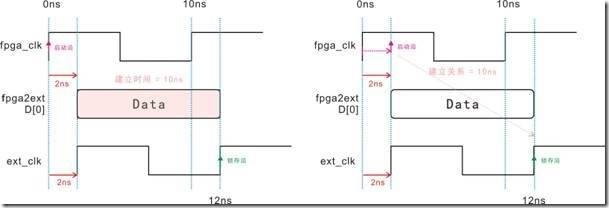
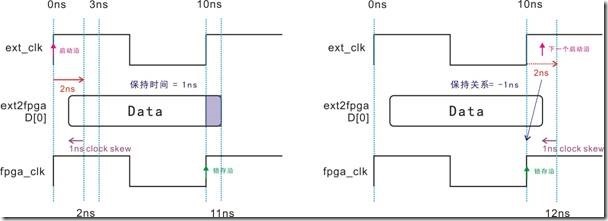
图5.3.7 ext_clk右移，建立时间与建立关系的等价图。
除了数据信号会受延迟影响以外，同样时钟信号也会受延迟影响，图5.3.7是 ext_clk信号受2ns延迟的结果 ... 左图中，ext_clk受延迟影响而向右移动2ns，结果建立时间为10ns；换之，右图是建立关系的等价图，亦即由于ext_clk受2ns延迟的影响，锁存沿也从原本10ns的位置，移至12ns，结果造成建立关系为10ns。
这种看法是不伤大雅的碎事，不过对于TimeQuest而言，尤其是计算上 ... 我们知道 TimeQuest是利用 Setup Relationship（建立关系）与Hold Relationship（保持关系）作为计算的参考和补助（或者简化），单是数据信号跑来跑去TimeQuest已经够烦了，如果时钟再参一脚也跑来跑去的话，结果会造成TimeQuest 会抓狂的,为此 ...
===================================================================
师弟：我说，师兄呀 ... TimeQuest 在计算的时候，有没有利用“手段”，不让时钟跑来
跑来去，而只让数据跑来跑去？
师兄：什么跑来跑去？你的意思是不是说“让时钟信号的延迟变化影响在数据身上”，
亦即TimeQuest计算时，时钟信号位置基本不变，不过时钟信号受延迟影响的结
果直接叠加在数据信号身上？
师弟：真不愧是我的偶像，那么快就悟出本意 ...
师兄：少拍马屁了 ... 不过，TimeQuest确实有用“手段”！
师弟：手段？什么样的手段？我很好奇!
（ 师弟的眼睛睁得大大的 ... ）
师兄：在Fmax的章节中，有没有了解过 Clock Skew？
师弟：有是有 ... clock skew 就是目的寄存器clk相减源寄存器clk的时钟差，对否？
师兄：正解！
师弟：不过，师兄啊 ... 我虽然知道 clock skew 的定义而已，但不晓得实际用途却。
师兄：fmax与clock skew放在一起谈的确意义不大，毕竟影响fmax的凶手还是组合
逻辑的延迟压力。
师弟：那么，clock skew 的实际用途是甚麽？
师兄：嘛，别急师弟，让我们看akuei2如何解释 ...
（师兄话玩用手指着电脑屏幕 ... ）
===================================================================
clock skew 的定义正如师弟所言“的寄存器clk相减源寄存器clk的时钟差”，为方便笔者就称呼“时钟差”，然而 clock skew 的公式如下所示。clock skew结果最终会直接作用在数据的延迟上。
clock skew = < destination reg clock delay > - < source reg clock delay >
时钟差 = <源寄存器时钟源延迟> - < 目的寄存器时钟源延迟 >
对 fpga2ic 的外模型而言，fpga_clk 是源寄存器时钟然而ext_clk 是目的寄存器时钟。从图5.3.7中我们可以知道 fpga_clk 的延迟是0ns，而 ext_clk 的延迟是2ns，clock
skew取值自然是 2ns。
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = <ext_clk delay> - < fpga_clk delay>
= (2 - 0)ns
= 2ns
data delay = 2ns
data delay' = <data delay> - <clock skew>
= 2ns - 2ns
= 0ns
data delay 数据延迟
data delay' 时钟差作用后的数据延迟
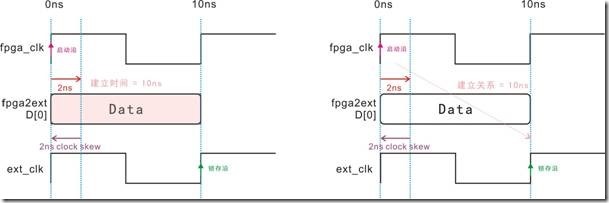
图5.3.8 clock skew，建立时间与建立关系的等价图。
图5.3.8是图5.3.7受 clock skew 作用以后，建立时间与建立关系的等价图。从中我们可以知道fpga_clk 还有 ext_clk 不再跑来跑去，换之原本向右移动2ns的D[0]，受时钟差2ns作用以后的位置是0ns。结果造成建立时间为10ns，至于右图的启动沿也受到时钟差的作用，从原本的2ns返回0ns，最终建立关系取得10ns。
图5.3.8的建立时间与建立关系结果，基本上和图5.3.7的建立时间与建立关系一模一样。
这下 clock skew真的神了 ... “欸，笔者！clock skew 真的那么神吗？还是你老子在故弄玄虚？”爷爷我是不骗人的，不信吗？好，让我们再实验看看 ..
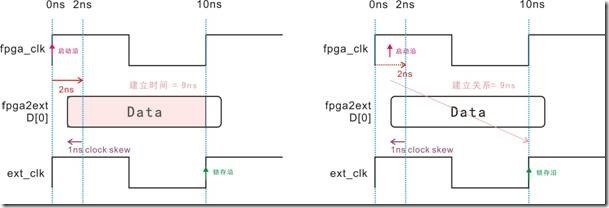
图5.3.9 fpga_clk与ext_clk右移，建立时间与建立关系的等价图。
图5.3.9左图中的fpga_clk 延迟1ns；ext_clk延迟2ns；D[0]的延迟还是之间的2ns。结果而言，Data的建立时间是9ns。然而右图中，启动沿不仅受D[0]的2ns延迟，也受fpga_clk的1ns延迟影响，结果启动沿从原本的0ns变成3ns。不过，锁存沿本身也受ext_clk的2ns延迟影响，最终取得的建立关系是9ns。然后让我们来计算一下 clock skew 与 data delay'
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = <ext_clk delay> - < fpga_clk delay>
= (2 - 1)ns
= 1ns
data delay = 2ns
data delay' = <data delay> - <clock skew>
= 2ns - 1ns
= 1ns
图5.3.10 clock skew，建立时间与建立关系的等价图。
图5.3.10是图5.3.9受时钟差作用下的结果，左图中的 Data 从原本的2ns延迟，由于受到时钟差影响，结果延迟变成1ns，最终建立时间取得9ns。换之，右图中的启动沿原本位置是2ns，不过受到时钟差的影响，结果退回1ns，建立关系从而得到9ns。好了，让我们在一次比较图5.3.10和图5.3.9的建立时间与建立关系，答案是不是一样呢？这回信服了吧，哇咔咔咔！哇咔咔咔！
同学们现在还不能放心，目前我们只是了解到 clock skew如何影响数据的延迟，从而使得图5.3.10是图5.3.9的建立时间和建立关系取得同样结果 ... 如果换个角度来想 clock skew作用现象也是不是会发生在保持时间与保持关系的身上呢？本当に興味深い。
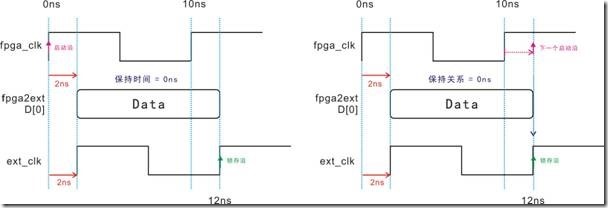
图5.3.11 ext_clk右移，保持时间与保持关系的等价图。
图5.3.11左图是ext_clk 同D[0]延迟2ns，结果造成保持时间为0ns。然而右图中的下一个时间沿虽然受到2ns的延迟，从原本的10ns变成12ns，不过由于 ext_clk 也有2ns的延迟，保持关系最后取得0ns。接下来，让我们计算一下时间差和受作用以后的 data delay:
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = <ext_clk delay> - < fpga_clk delay>
= (2 - 0)ns
= 2ns
data delay = 2ns
data delay' = <data delay> - <clock skew>
= 2ns - 2ns
= 0ns
图5.3.12 clock skew，保持时间与保持关系的等价图。
图5.3.12 与 图5.3.11 的保持时间和保持关系对于之下，同样的答案，同样的结果，不同的只是发生经过。图5.3.12的左图，数据原本受2ns的延迟以后应该在2ns的位置，可是被 2ns的时钟差绊了一道以后变回到0ns的位置，从而取得0ns的保持时间。换之，右图中的下一个启动沿原本受2ns的延迟以后，位置应该是12ns才是，可是不小新绊到 2ns的时钟差便跌回10ns的位置，结果页造成0ns的保持关系。
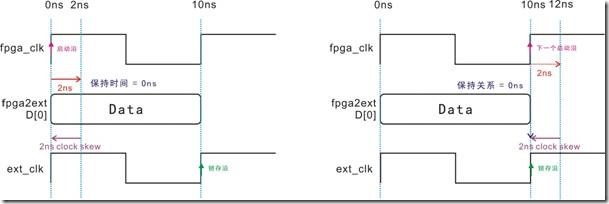
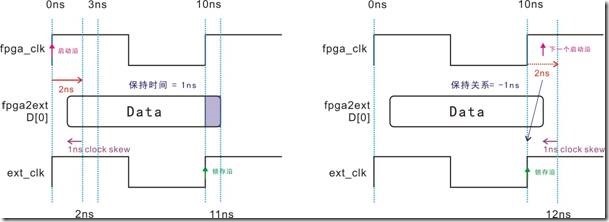
图5.3.13 fpga_clk 和 ext_clk右移，保持时间与保持关系的等价图。
图5.3.13左图中由于fpga_clk 受延迟1ns，ext_clk受延迟2ns，结果造成保持时间为1ns
。换之，由图中的下一个启动沿由于受到fpga_clk的延迟，再加上D[0]的延迟，最终停留在13ns的位置，不过锁存沿也受到 ext_clk 延迟2ns的影响，从而保持关系成为-1ns。
还是先计算时钟差和受作用以后的data_delay' ...
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = <ext_clk delay> - < fpga_clk delay>
= (2 - 1)ns
= 1ns
data delay = 2ns
data delay' = <data delay> - <clock skew>
= 2ns - 1ns
= 1ns
图5.3.14 clock skew，保持时间与保持关系的等价图。
图5.3.14与图5.3.13相较之下，同样的保持时间，同样的保持关系，不同的只是发生经过 ... 左图中的D[0]受2ns的延迟，原先位置应该在2ns才对，不过由于受到时间差1ns的作用，结果退回到1ns的地方，最终取得1ns的保持时间。换之，右图的下一个启动沿，原本受2ns的延迟，位置应该在12ns才是，不过它不小心撞到1ns的时间差，就这样跌在11ns的位置，最后也不小心取得-1ns的保持关系。
嘻嘻，经过那么多实验 ... 同学们也该相信笔者不在故弄玄虚吧！？笔者想必许多同学一定很好奇，这章节我们不是应该在谈有关外部模型和外部延迟有关的种种吗？为什么无缘无故又扯上那么多稀奇古怪的内容？嘛 ... 别着急，这些都是最基本知识，习得它以后同学们就可以飞天遁地了。
5.4 外部模型②
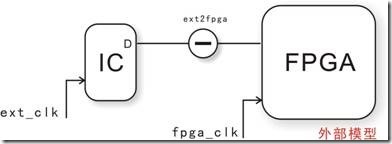
图5.4.1 ic2fpga（ext2fpga）的外部模型。
在章节5.3的时候，我们已经谈过 fpga2ic的外部模型，还有建立时间，建立关系，保持时间，保持关系，或者clock skew作用等内容。然而这章节将要讨论的是 ic2fpga 外部模型，至于内容基本上与fpga2ic大同小异而已，fpga2ic与ic2pfga之间的差别就在fpga与ic的角色扮演换了位置而已：fpga2ic是fpga输出数据ic读；ic2fpga是ic输出数据fpga读。
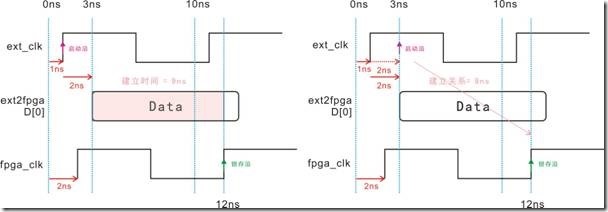
图5.4.2 ext_clk和fpga_clk 右移，建立时间与建立关系的等价图。
图5.4.2是不是很眼熟？那当然，笔者只是替图5.3.9换张皮而已，不过习惯上还是随便解释一下。左图中的ext_clk受1ns延迟，而fpga_clk受2ns延迟，再加上D[0]的2ns延迟，最终导致建立时间为9ns。换之右图中的启动沿，受D[0]延迟2ns再加上ext_clk延迟1ns的影响，结果位于3ns ... 不过 fpga_clk也受2ns的延迟，最后建立关系取得9ns的成绩。
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = < fpga_clk delay> - <ext_clk delay>
= (2 - 1)ns
= 1ns
data delay = 2ns
data delay' = <data delay> - <clock skew>
= 2ns - 1ns
= 1ns
图5.4.3 clock skew, 建立时间与建立关系的等价图。
图5.4.3是图5.4.2受clock skew影响的时序图。ext_clk 与 fpga_clk时钟差是1ns，这个时钟左右了原先位置应该在2ns的D[0]，不小心倒回1ns的位置，最后取得9ns的建立时间。换之，右图中的启动沿原先受D[0]的2ns延迟，位置应该落在2ns才是，不过被1ns的时间差绊了一脚，然后跌在1ns的位置，因此取得9ns的建立关系。
图5.4.4 ext_clk 与 fpga_clk 右移，保持时间与保持关系的等价图。
不要怀疑，图5.4.4同是图5.3.13的换皮结果 ... 左图中，由于D[0]受到自身2ns的延迟，还有ext_clk延迟的影响，导致起跑线在3ns，而fpga_clk也受2ns的延迟，最后导致保持时间为1ns；换之，右图中的下一个启动沿由于受到 1ns的ext_clk 延迟，再加上D[0]本身的2ns延迟，结果下一个启动沿的位置从13ns开始，不过由于fpga_clk也受到2ns延迟的影响，最终保持关系取得-1ns。
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = < fpga_clk delay> - <ext_clk delay>
= (2 - 1)ns
= 1ns
data delay = 2ns
data delay' = <data delay> - <clock skew>
= 2ns - 1ns
= 1ns
图5.4.5 clock skew，保持时间与保持关系的等价图。
图5.4.5是图5.4.4受clock skew 作用以后的时序图。左图中的D[0]原本应该从2ns的位置起跑，可是不小心踩到1ns的时间差，然后跌倒在1ns的位置，从而造就1ns的保持时间。换之，由图中的下一个启动沿，原受到2ns的延迟而在12ns的位置，结果还是一样衰，不小心踩到1ns的时间差，然后跌在11ns的位置，最后导致保持关系为-1ns。
到目前为止，我们只是在了解单位宽信号（数据）的传输而已 ... 更多时候，信号位宽都是N*字节为单位，因此我们有必要好好学习一下TimeQuest是如何“应付”这些多位宽的数据呢？
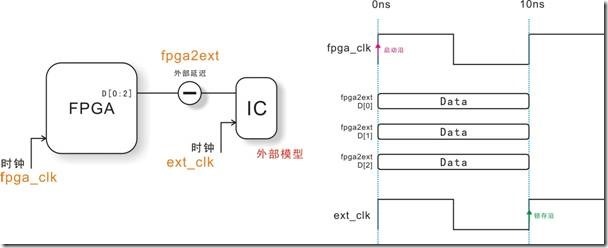
图5.4.6 fpga2ic外部模型的多位宽数据传输。
图5.4.6左图相较上一章节的fpga2ic的外部模型不是D[0]而是D[0:2]，也就是多位宽数据传输，然而右图是多位宽传输的理想时序图（fpga向ic发送3位10ns周期的数据/信号）。
TimeQuest认识单位宽传输与多位宽传输的方法基本上是大同小异，换句话说 ... 某个单位宽重复n次后就会成为多位宽。笔者知道自己在说废话，不过也就是这句废话让笔者领悟到，TimeQuest不会那么努力一个一个去识别单位宽，而且我们也不可能逐个逐个将单位宽告诉TimeQuest ... 不然我们和TimeQuest都会抓狂。因此TimeQuest在应付多位宽的时候偷偷用“手段”？这个“手段”又是什么呢？
图5.4.7 均为与不均匀的延迟压力。
假设fpga2ext的路上存有延迟，结果造成数据D向右移动，这时候我们会遇见延迟压力均匀与不均匀的问题，延迟压力均匀如图5.4.7左图所示，换之延迟压力不均匀如图5.4.7右图所示。延迟压力如果均匀的话，不仅在审美上，绘制时序图上，还是JDL在时序产生上，都非常便利。相反的，如果延迟压力不均匀的话，在许多方面上会麻烦一点。
笔者在《整合篇》中曾经举例过，自定义的乘法器比起传统的乘法器更容易控制延迟压力均匀与否。当然所谓的延迟压力均匀不是图5.4.7的左图中出现一样 ... 那么完美的数值，实际上会是2.8ns，2.9ns，3.1ns等接近3ns的数值。事实上，延迟压力均不均匀只是完美主义的追求而已，对实际的影响不大，话虽如此 ... 不过可以的话笔者也会努力去均匀一点各个延迟压力，毕竟这样看会比较顺眼一点~笑。
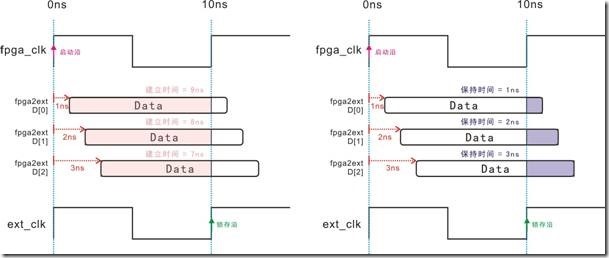
图5.4.8 延迟压力不均匀与建立时间和保持时间的关系。
让我们切回主题 ... 延迟压力不均匀是时序的家常便饭，图5.4.7的右图告诉我们最大的延迟是 D[2] 的3ns，最小的延迟是D[1] 的1ns。因此，我们可以这样说道：
D[0..2] delay max = 3ns;
D[0..2] delay min = 1ns;
图5.4.8是延迟压力不均匀给建立时间和保持时间造成的影响。让我们来思考吧 ... 图5.4.8 的左图中，有3个信号（数据），D[0]的建立时间为9ns，D[1]的建立时间为8ns，还有D[2]的建立时间为7ns。“请问哪一个数据的建立时间最危险的？”，在物理时序角度上，亦即建立时间越少越危险，我们当然将矛头指向D[2]。
图5.4.8的右图中，同样也是3个信号，D[0]的保持时间为1ns，D[2]的保持时间为2ns，D[3]的保持时间为3ns。“请问哪一个数据的保持时间是最危险的？”，在物理时序角度上思考，亦即保持时间越少越危险，结果最危险的保持时间自然是D[0]。因此我们可以这样结论：在D[0]~D[2]三个位宽中，delay max 影响建立时间（建立关系）, delay min 影响保持时间（保持关系）。
“欸 ... 笔者怎么搞的？我越来越搞糊涂了”这个问题一定会由心而生吧？呵呵 ... 笔者没有胡来，笔者也没有胡搞，同学们稍微回忆一下“fmax最差劲节点”的故事。事实上，上述的结论与“最差劲节点”都有相同的原理 ...
TimeQuest在分析D[0..2]建立时间的时候，它只要注意“最危险的建立时间”即可，按逻辑而言，没有什么比“最危险”更危险。同样思路，TimeQuest在分析D[0..2]保持时间的时候，它只要注意“最危险的保持时间”即可，因为没有什么比“最危险”更危险。
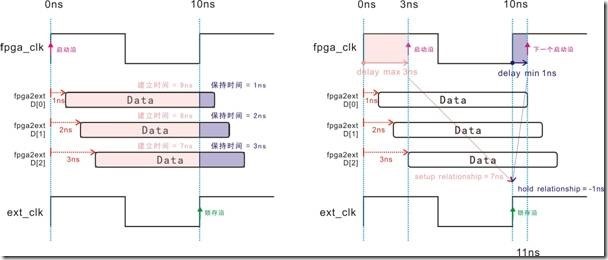
图5.4.9 （左）建立时间与保持时间，（右）建立关系与保持关系，之间的等价图。
图5.4.9左边是建立时间与保持时间的时序图，换之右边是建立关系与保持关系的等价图。笔者曾讲过，建立关系与保持关系的等价图事实上不怎么关心数据的死活，然而它们仅关心，启动沿，下一个启动沿，或者锁存沿的变动，还有建立关系和保持关系而已。
从右图中我们可以了解到，3ns延迟的delay max 影响启动沿从原本0ns 的位置，向右移至3ns。换之，1ns延迟的delay min 影响下一个启动沿从原本的 10ns位置，向右移至11ns。最终导致建立关系为7ns，保持关系为-1ns ... 这个结果与7ns的建立时间，1ns的保持时间不谋而合。
读到这里，笔者理解到许多同学可能一时之间无法消化这些莫名奇妙的东西 ... 说实话，笔者初次认识的时候也有同样的感觉，原本感觉莫名奇妙的东西经过多次研究以后，渐渐觉得“情有可原” ... 然后诚心接受了。从学习 Verilog 到至今再莫名奇妙的事情也遇过了，最终笔者领悟到一个道理，要用那个世界的自然思考那个世界的现象，不要用这个世界的自然思考那个世界的现象。
接下来让我们继续思考 .... clock skew 如何影响 delay max 与 delay min ？
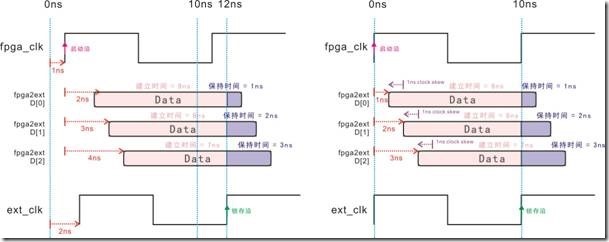
图5.4.10 Clock skew 影响建立时间与保持时间的时序图。
在图5.4.10的左图中，fpga_clk有1ns的延迟，ext_clk有2ns的延迟，然而D[0]有2ns的延迟，D[1]有3ns的延迟，D[2]有4ns的延迟。各种延迟与数据相互作用以后，D[0]取得9ns的建立时间，1ns的保持时间；D[1]取得8ns的建立时间，2ns的保持时间；D[2]取得7ns的建立时间，3ns的保持时间。接下来，让我们先计算一下 clock skew ...
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = <ext_clk delay> - < fpga_clk delay>
= (2 - 1)ns
= 1ns
clock skew 的结果为1ns，结果D[0..2]的延迟都被绊了一脚，通通向后移动1ns，结果如图5.4.10的右图所示。虽然左图与右图拥有同样的建立时间与保持时间，不过它们的差别就在于左图的时钟跳来跳去，换之右图的时钟固步不动。
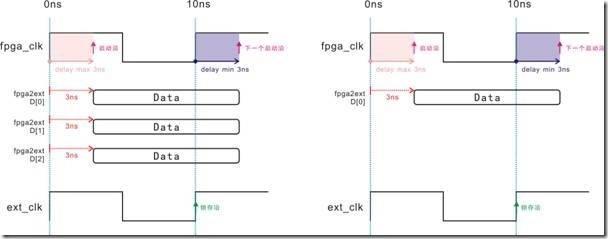
图5.4.11 clock skew 影响建立关系与保持关系的时序图。
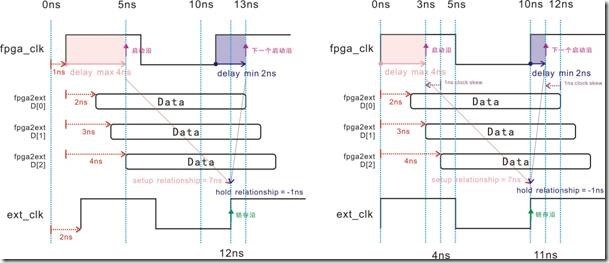
图5.4.11的左图是未曾受 clock skew 影响的建立关系与保持关系的时序图，其中fpga_clk，ext_clk与D[0..2]的延迟与上述一样。差别就在左图中，启动沿受4ns延迟的 delay_max影响，再加上 fpga_clk的1ns延迟，结果落在5ns的位置；然而下一个启动沿，受2ns延迟的delay min影响，结果落在13ns的位置。ext_clk有2ns的延迟，因此锁存沿的位置也在于12ns。最后建立关系取得7ns，保持关系取得 -1ns。
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = <ext_clk delay> - < fpga_clk delay>
= (2 - 1)ns
= 1ns
clock skew 与上述一样是1ns ... 右图中的fpga_clk 与ext_clk固步不动在0ns位置，原本受delay max影响的启动沿应该落在4ns的位置，可是它不小心撞到1ns的时间差，最后跌倒在3ns的地方；换之，原本受delay min 影响的的下一个启动沿，同样也不小心撞到1ns的时间差，从12ns的位置跌到11ns的位置。最终取得 7ns的建立关系，还有 -1ns的保持关系。左图与右图之间的差别就在于左图的 fpga_clk 与 ext_clk都跳来跳去，换之右图的fpga_clk 与 ext_clk都乖乖呆在原地。
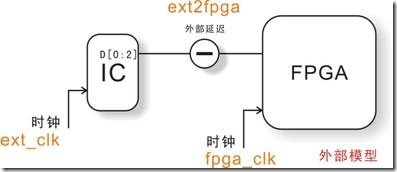
图5.4.12 ic2fpga（ext2fpga）多位宽的外部模型。
在前面我们解了有关 fpga2ic与多位宽，这回合让我们来了解一下有关ic2fpga与多位宽的种种。图5.4.12 是多位宽ic2fpga的外部模型，事实上它与多位宽fpga2ic的外部模型只是换个角色，换个位置而已，大体上都是换汤不换药。不过笔者还是惯例的讲一讲 ...
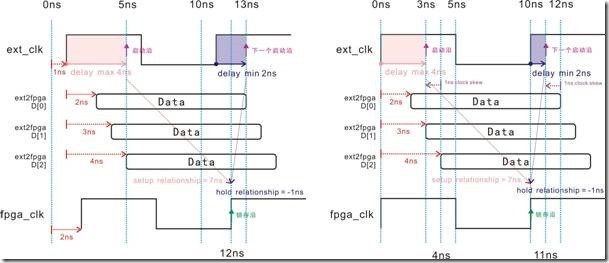
图5.4.13 （ic2fpga）clock skew 影响建立关系与保持关系的时序图。
图5.4.13与图5.4.12基本上只是更换一下D[0..2]的名字还有ext_clk与fpga_clk的位置而已，其他都一模一样。在左图中，ext_clk受1ns的延迟，fpga_clk受2ns的延迟，然而D[0..2]接续有2ns~4ns的延迟。启动沿不仅受ext_clk延迟1ns的影响，它更受delay max的阻拦从而落在5ns的位置。至于下一个启动沿同样也受到ext_clk延迟1ns的影响，它接着又被 delay min妨碍，结果落在13ns的位置。最终取得7ns的建立关系，还有 -1
ns的保持关系。
clock skew = < destination reg clock delay > - < source reg clock delay >
clock skew = <fpga_clk delay> - <ext_clk delay>
= (2 - 1)ns
= 1ns
clock skew 经过计算以后取值为1ns。至于5.4.13的右图是启动沿与下一个启动沿受时钟差左右的时序图 ... 原本受4ns delay max延迟的启动沿，由于不小心被1ns的时钟差绊倒，从4ns的位置跌至3ns的位置。换之下一个启动沿原本受2ns的delay max延迟，同样也不小心撞到1ns的时钟差，结果从原本12ns的位置跌至11ns的位置。最后取得
7ns的建立关系，还有 -1 的保持关系。
到目前位置，我们已经了解完相关的基础知识，接下来我们不仅会推导公式，还会学习有关的约束命令，亦即 set_input_delay 与 set_output_delay。同学们，笔者还是建议先歇一会吧，好让自己的脑袋冷静一下，就算战意高昂也不要勉强自己，任何时候都不要高估自己的能力。
5.5 推导外包资料的公式
想必任何人都不喜欢推导公式吧？说实话，笔者也是 ... 不过接下来我们要推导的不是数学公式，而是与外部模型有关的公式。这样做不是为了什么，而是为了让同学们进一步认识外部模型。
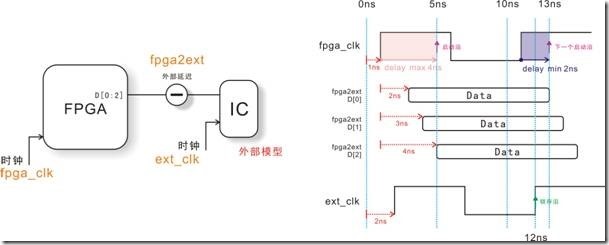
图5.5.1 fpga2ic的外部模型（左），有各种延迟的时序图。
图5.5.1的左图是fpga2ic的外部模型，然而右图是相关的时序图 ... 从右图中，我们可以取得以下信息：
fpga_clk delay 1ns
ext_clk delay 2ns
fpga2ext D[0] 2ns (delay min)
fpga2ext D[1] 3ns
fpga2ext D[2] 4ns (delay max)
信息取得以后，我们就要开始推导公式了 ... fpga2ic的外部模型从另一个角度来看是 fpga 输出数据，ic读取数据。然而公式的推导都以fpga为主要，因此fpga2ic 的公式又称 output 公式，但是output公式又应该针对什么呢？很简单，output 公式主要是针对5.5.1右图中的启动沿，与下一个启动沿。
针对启动沿的output公式又名 output max，换之针对下一个启动沿的output公式又名 output min。
output max = <fpga2ext delay max>
output min = < fpga2ext delay min >
output max 与 min的公式目前还是很单纯，因为我们还没有将 clock skew 考虑进去。
![clip_image088[1]](http://images0.cnblogs.com/blog/494276/201312/02173839-294e0cb120064c29a677ebf1eda21661.jpg "clip_image088[1]")
图5.5.2 clock skew 与启动沿和下一个启动沿的关系。
图5.5.2的左图是还没有将 clock skew 考虑进去的时序图，其中fpga_clk的延迟有1ns，ext_clk的延迟有2ns，经过计算以后clock skew 值是1ns。然而右图是左图与 clock skew 相互作用以后的结果，无论是启动沿还是下一个启动沿，它们都不小心撞到1ns的时钟差，然后向后移动1ns。
clock skew 无差别对待启动沿与下一个启动沿，换句话说clock skew 无论是output max 或者 output min它都看不顺眼，因此：
output max = <fpga2ext delay max> - < destination reg clk delay - source reg clk delay >
= <fpga2ext delay max> - < ext_clk delay - fpga_clk delay >
= <fpga2ext delay max> - < clock skew >
output min = < fpga2ext delay min > - < destination reg clk delay - source reg clk delay >
= <fpga2ext delay min> - < ext_clk delay - fpga_clk delay >
= <fpga2ext delay min> - < clock skew >
|
|
|
图5.5.3 Tsu影响建立关系（左），Th影响保持关系（右）。
就算是外部ic，凡是有IO口就有寄存器，凡是有寄存器一定有寄存器特性，因此外部ic的寄存器一定有参数 Tsu 和 Th。Tsu粗略点讲，它是影响建立关系的寄存器参数；换之，Th粗略点将，它是影响保持关系的寄存器参数（如图5.5.3所示）。要将Tsu与Th加入 output min 与 output max公式，建立关系和保持关系是关键。
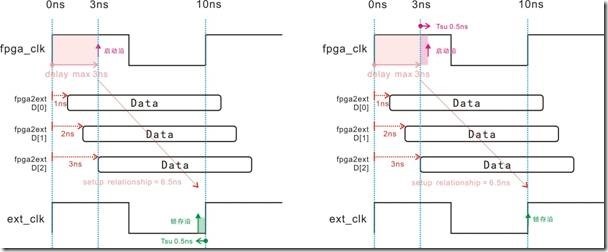
图5.5.4 Tsu影响建立关系，Tsu影响启动沿（output max）的等价关系。
5.5.4的左图是启动沿受 delay max 影响后落在3ns的位置，由于外部ic的寄存器也存有0.5ns的Tsu参数，结果导致锁存沿向左移动0.5ns，然后落在9.5ns的位置，最终得到得到6.5ns的建立关系。换之右图中的锁存沿固步不动，不过0.5ns的Tsu却影响原先停留在3ns位置的启动沿，启动沿就这样迷迷糊糊的向右移动0.5ns，然后落在3.5ns的位置。最终得到6.5ns的建立关系。
图5.5.5 Th影响保持关系，Th影响下一个启动沿（output min）的等价关系。
图5.5.5的左图，下一个启动沿原本受1ns的delay min 影响，接着移动到11ns的位置。此外，锁存沿不小心受到0.5ns的Th影响，结果锁存沿移向10.5ns的位置，最终得到 -0.5ns的保持关系。至于右图中的锁存沿却丝毫不动，可是原本已经受 delay min影响的下一个启动沿，这下也受Th那0.5ns的影响，然后落在10.5ns的地方，最终得到 -0.5ns的保持关系。
从上述的过程中，我们知道Tsu影响启动沿也间接影响 output max；Th反而影响下一个启动沿也间接影响 output min ... 因此，output max 和 output min 的公式可以这样更动：
output max = <fpga2ext delay max> - < destination reg clk delay - source reg clk delay > + ext_Tsu
= <fpga2ext delay max> - < ext_clk delay - fpga_clk delay > + ext_Tsu
= <fpga2ext delay max> - < clock skew > + ext_Tsu
output min = < fpga2ext delay min > - < destination reg clk delay - source reg clk delay > - ext_Th
= <fpga2ext delay min> - < ext_clk delay - fpga_clk delay > - ext_Th
= <fpga2ext delay min> - < clock skew > - ext_Th
ext_Tsu 别名 ic_Tsu 亦即外部ic寄存器的 Tsu
ext_Th 别名 ic_Th 亦即外部ic寄存器的 Th
图5.5.6 延迟压力均衡（左），当单位宽（右）。
图5.5.6是延迟压力均匀（作）与单位宽（右）的时序图 ... 对于均与的延迟压力来说，没有所谓的 delay max 与 delay min之分，反过来说 delay max 是 delay min，或者 delay min 是 delay max。至于单位宽来也没有所谓的 delay max 与 delay min，又或者说delay max 与 delay min 相等。
这种情况我们称为 delay both，换句话说 delay both 皆是 delay max 与 delay min，因此 output max 与 output min 可以这样更动（both英文是皆是的意思）：
output max = <fpga2ext delay max> - < destination reg clk delay - source reg clk delay > + ext_Tsu
= <fpga2ext delay max> - < ext_clk delay - fpga_clk delay > + ext_Tsu
= <fpga2ext delay max> - < clock skew > + ext_Tsu
//等价//
output max = <fpga2ext delay min> - < destination reg clk delay - source reg clk delay > + ext_Tsu
= <fpga2ext delay min> - < ext_clk delay - fpga_clk delay > + ext_Tsu
= <fpga2ext delay min> - < clock skew > + ext_Tsu
//等价//
output max = <fpga2ext delay both> - < destination reg clk delay - source reg clk delay > + ext_Tsu
= <fpga2ext delay both> - < ext_clk delay - fpga_clk delay > + ext_Tsu
= <fpga2ext delay both> - < clock skew > + ext_Tsu
output min = < fpga2ext delay max > - < destination reg clk delay - source reg clk delay > - ext_Th
= <fpga2ext delay max> - < ext_clk delay - fpga_clk delay > - ext_Th
= <fpga2ext delay max> - < clock skew > - ext_Th
//等价//
output min = < fpga2ext delay min > - < destination reg clk delay - source reg clk delay > - ext_Th
= <fpga2ext delay min> - < ext_clk delay - fpga_clk delay > - ext_Th
= <fpga2ext delay min> - < clock skew > - ext_Th
//等价//
output min = < fpga2ext delay both > - < destination reg clk delay - source reg clk delay > - ext_Th
= <fpga2ext delay both> - < ext_clk delay - fpga_clk delay > - ext_Th
= <fpga2ext delay both> - < clock skew > - ext_Th
延迟压力均匀与单位宽是比较特殊的状况，不过道理上和不均匀的多位宽一样。
读到这里笔者猜想，一定有同学会觉得非常奇妙，fpga2ic是指fpga发送数据给ic“为什么在加入外部ic寄存器的 Tsu 与 Th 参数时，却没有考虑过 fpga 本身的Tco寄存器参数？”原因很单纯，不是我们不考虑事实上TimeQuest已经了解了，因为 output 公式是以 fpga为主要，换句话说Tco是fpga的内部延迟因数，所以我们不用刻意告诉它。
![clip_image090[1]](http://images0.cnblogs.com/blog/494276/201312/02173842-19995ed7c5ee4ea7a8c97576be956228.jpg "clip_image090[1]")
图5.5.7 ic2fpga（ext2fpga）的外部模型。
ic2fpga是ic发送数据，fpga读取数据的外部模型，不过不管位置怎么改变，大体上都是大同小异而已。ic2fpga依然也是fpga为主要，亦即fpga读取数据，因此也称为 input 公式。同样，针对启动沿的input 公式称为 input max；换之，针对下一个启动沿的 input 公式称为 input min。
input max = <ext2fpga delay max> - < destination reg clk delay - source reg clk delay >
= <ext2fpga delay max> - < fpga_clk delay - ext_clk delay >
= <ext2fpga delay max> - < clock skew >
input min = < ext2fpga delay min > - < destination reg clk delay - source reg clk delay >
= <ext2fpga delay min> - < fpga_clk delay - ext_clk delay >
= <ext2fpga delay min> - < clock skew >
|
|
|
![clip_image096[1]](http://images0.cnblogs.com/blog/494276/201312/02173843-7b0a2d900fb343c583b1d8aeab85c640.jpg "clip_image096[1]")
![clip_image098[1]](http://images0.cnblogs.com/blog/494276/201312/02173844-9519fe7bcc0e4feea4afc2ca074f45e6.jpg "clip_image098[1]")
图5.5.8 Tco影响建立关系（左），Tco影响保持关系（右）。
ic2fpga的外部模型，外部ic是发送方，因此我们必须考虑外部ic的Tco寄存器参数。如图5.5.8所示，无论是建立关系还是保持关系都会路出Tco的笑脸。
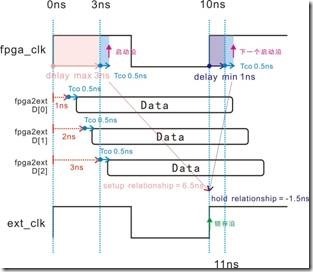
图5.5.9 Tco影响建立关系与保持关系。
Tco是比较霸道的寄存器参数，它吃定建立关系与保持关系。从图5.5.9中我们可以理解到，0.5ns的Tco助长了1ns的delay min 成为1.5ns，同样 Tco也助长了 3ns的delay max成为3.5ns。以此类推，启动沿受 delay max 影响，而且delay max 的新值是 3ns + 0.5ns，亦即3.5ns。换之下一个启动沿受 delay min影响，而且delay min 的新值是 1ns + 0.5ns，亦即1.5ns。最终导致建立关系为6.5ns，保持关系为 -1.5ns。
因此input max 与 input min 公式可以这样更动：
input max = <ext2fpga delay max> - < destination reg clk delay - source reg clk delay > + ext_Tco
= <ext2fpga delay max> - < fpga_clk delay - ext_clk delay > + ext_Tco
= <ext2fpga delay max> - < clock skew > + ext_Tco
input min = < ext2fpga delay min > - < destination reg clk delay - source reg clk delay > + ext_Tco
= <ext2fpga delay min> - < fpga_clk delay - ext_clk delay > + ext_Tco
= <ext2fpga delay min> - < clock skew > + ext_Tco
//等价//
input min = < ext2fpga delay min > - < destination reg clk delay - source reg clk delay > + ext_minTco
= <ext2fpga delay min> - < fpga_clk delay - ext_clk delay > + ext_minTco
= <ext2fpga delay min> - < clock skew > + ext_minTco
ext_Tco 别名 ic_Tco 亦即外部ic的Tco寄存器参数。
ext_minTco 别名 ic_minTco 亦即外部ic的最小Tco寄存器参数。
同学们可能会举得疑惑，为什么 input min 会有另一个等价的公式，还有 minTco又是什么？minTco是Tco的最小值，但是差别的比率，根据硬件的不同，结果也会不同。
按照理论，input min 载入 ext_Tco 还是 ext_minTco都没有问题。实际上，载入 ext_Tco 比起载入 ext_minTco 有更好的保险作用。既然如此，为什么 ext_minTco 还受到重用呢？关于这点笔者就不怎么清楚了，可能是近似作用或者其他的吧 ... 无论怎样选择都是见仁见智了。
5.6 外部模型的input/ouput 约束指令
这一章我们将通过假想的实验来认识外部模型的input/output 约束命令。
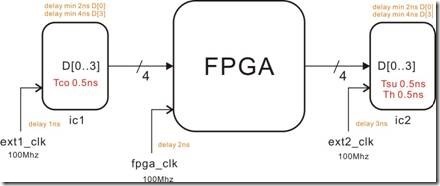
图5.6.1 假想实验的外部模型。
图5.6.1是假想实验的外部模型，fpga与ic2是 fpga2ic的关系，亦即fpga经过D[0:3]发送数据给ic2。然而D[0..3]之间，delay min 是2ns，然而delay max 4ns，至于ic2的寄存器特性是0.5ns的Tsu和0.5ns的Th。换之 ic1与fpga是fpga2ic的关系，亦即ic1经过D[0:3]发送数据给fpga，其中 delay min 是2ns，delay max 是4ns，此外ic1有0.5ns的Tco。
ext1_clk 是受1ns延迟的100Mhz时钟；fpga_clk是受2ns延迟的100Mhz时钟；ext2_clk是受3ns延迟的100Mhz时钟。然后让我们计算一下 input/output min/max的各种取值：
delay min 2ns
delay max 4ns
ext1_clk delay 1ns
fpga_clk delay 2ns
ext2_clk delay 3ns
Tco/Tsu /Th 0.5ns
input max = <ext2fpga delay max> - < destination reg clk delay - source reg clk delay > + ext_Tco
= <ext2fpga delay max> - < fpga_clk delay - ext1_clk delay > + ext_Tco
= <ext2fpga delay max> - < clock skew > + ext_Tco
= 4ns - (2ns - 1ns) + 0.5ns
=3.5ns
input min = < ext2fpga delay min > - < destination reg clk delay - source reg clk delay > + ext_Tco
= <ext2fpga delay min> - < fpga_clk delay - ext1_clk delay > + ext_Tco
= <ext2fpga delay min> - < clock skew > + ext_Tco
= 2ns - (2ns - 1ns) + 0.5ns
= 1.5ns
output max = <fpga2ext delay max> - < destination reg clk delay - source reg clk delay > + ext_Tsu
= <fpga2ext delay max> - < ext2_clk delay - fpga_clk delay > + ext_Tsu
= <fpga2ext delay max> - < clock skew > + ext_Tsu
= 4ns - (3ns - 2ns) + 0.5ns
= 3.5ns
output min = < fpga2ext delay min > - < destination reg clk delay - source reg clk delay > - ext_Th
= <fpga2ext delay min> - < ext_clk1 delay - fpga_clk delay > - ext_Th
= <fpga2ext delay min> - < clock skew > - ext_Th
= 2ns - (3ns - 2ns) - 0.5ns
= 0.5ns
实验六 假想实验 input/output delay约束
center_module.v
1. module center_module 2. ( 3. input CLK, 4. input RSTn, 5. input [3:0]Din, 6. output [3:0]Dout 7. ); 8. /********************************************/ 9. 10. reg [3:0]rData; 11. 12. always @ ( posedge CLK or negedge RSTn ) 13. if( !RSTn ) 14. begin 15. rData <= 4'd0; 16. end 17. else 18. begin 19. rData <= Din; 20. end 21. 22. /********************************************/ 23. 24. assign Dout = rData;
上述是 center_module.v 的内容，乍看下 fpga 也只是充当 ic1与ic2之间的间接寄存器而已。亦即从ic1读入数据致 rData，然后又将rData的数据发送给ic2。
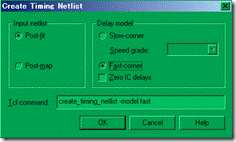
图5.6.2 创建 best case 网表。
再来先创建同名的 center_module.sdc 文件，然后将它设置为本实验的约束文本，再来打开TimeQuest。然后手动建立 best case 网表，如图5.6.2所示。
|
|
|
|
|
|
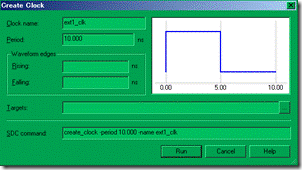
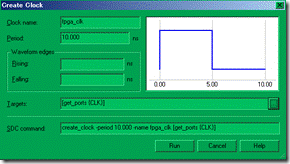
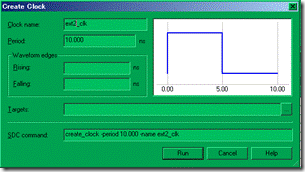
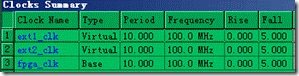
图5.6.3 创建3个时钟。
再来建立3个时钟（如图5.6.3所示），它们分别为是 10ns周期的 fpga_clk，ext1_clk还有 ext2_clk。除了fpga_clk是拥有对应的target以外（CLK的io），ext11_clk 与 ext2_clk 都是没有对应目标的 virtual clock（虚拟时钟）。
|
|
|
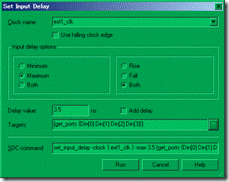
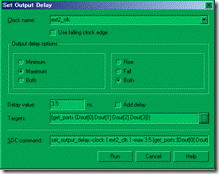
图5.6.4 set_input_delay 界面。
接下来，从Constraints 菜单中调出 set_input_delay界面（图5.6.4）。任何初次看到这张界面的同学，估计都会被奇奇怪怪的选项吓一跳，不过不要紧，让我们逐个来了解。
clock name 指向ic2fpga 外部模型中的ic时钟源，这里是 ext1_clk；至于 delay 选线中的 max 是指 input max，换之 min 是指 input min，而both 是指 min/max，接着在
delay value 中输入相关的数值，min 是 1.5ns，max是3.5ns；然而target是属于input 有关的输入口，在此是Din[0:3]。
图5.6.5 （左）默认，（右）use falling clock edge。
默认选项下 TimeQuest 都会认为被 clock name 指定的时钟都是上升沿触发（输出数据）。换之，使能 use falling clock edge，TimeQuest就会知道被 clock name 指定的时钟由下降沿触发。至于这个选项的用处暂时没有实例讲解，同学们先弄个大概就可以了。
至于 add_delay 选项是比较模糊的东西，一般上一个IO口都由1个寄存器驱动。不过一些特殊的IO口可能由多可寄存器驱动，例如 DDIO，亦即双沿IO口 ... 它里边是由2个寄存器同时驱动一个IO口，使能 add_delay 就是告诉TimeQuest某个IO由1个以上的寄存器驱动。至于rise/fall 或者 both 笔者就不清楚了，不过默认 both 就是了。
|
|
|
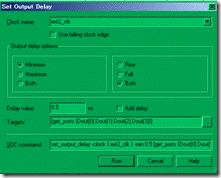
图5.6.6 set output delay 界面。
同样在 Constraints 菜单下调出 set output delay 的界面，如图5.6.6 所示。基本上 set input delay 与 set output delay 的意义差不多都一样，只是节点换了位置而已。其中clock name指定驱动外部ic的时钟，在这里是 ext2_clk。delay max 输入 3.5ns，delay min 则输入 0.5ns；target 则是 Dout[0:3]。完后，sdc文件会自动添加以下的约束命令，
center_module.sdc
#**************************************************************
# Create Clock
#**************************************************************
create_clock -name {fpga_clk} -period 10.000 -waveform { 0.000 5.000 } [get_ports {CLK}]
create_clock -name {ext1_clk} -period 10.000 -waveform { 0.000 5.000 }
create_clock -name {ext2_clk} -period 10.000 -waveform { 0.000 5.000 }
#**************************************************************
# Set Input Delay
#**************************************************************
set_input_delay -add_delay -max -clock [get_clocks {ext1_clk}] 3.500 [get_ports {Din[0]}]
set_input_delay -add_delay -min -clock [get_clocks {ext1_clk}] 1.500 [get_ports {Din[0]}]
set_input_delay -add_delay -max -clock [get_clocks {ext1_clk}] 3.500 [get_ports {Din[1]}]
set_input_delay -add_delay -min -clock [get_clocks {ext1_clk}] 1.500 [get_ports {Din[1]}]
set_input_delay -add_delay -max -clock [get_clocks {ext1_clk}] 3.500 [get_ports {Din[2]}]
set_input_delay -add_delay -min -clock [get_clocks {ext1_clk}] 1.500 [get_ports {Din[2]}]
set_input_delay -add_delay -max -clock [get_clocks {ext1_clk}] 3.500 [get_ports {Din[3]}]
set_input_delay -add_delay -min -clock [get_clocks {ext1_clk}] 1.500 [get_ports {Din[3]}]
#**************************************************************
# Set Output Delay
#**************************************************************
set_output_delay -add_delay -max -clock [get_clocks {ext2_clk}] 3.500 [get_ports {Dout[0]}]
set_output_delay -add_delay -min -clock [get_clocks {ext2_clk}] 0.500 [get_ports {Dout[0]}]
set_output_delay -add_delay -max -clock [get_clocks {ext2_clk}] 3.500 [get_ports {Dout[1]}]
set_output_delay -add_delay -min -clock [get_clocks {ext2_clk}] 0.500 [get_ports {Dout[1]}]
set_output_delay -add_delay -max -clock [get_clocks {ext2_clk}] 3.500 [get_ports {Dout[2]}]
set_output_delay -add_delay -min -clock [get_clocks {ext2_clk}] 0.500 [get_ports {Dout[2]}]
set_output_delay -add_delay -max -clock [get_clocks {ext2_clk}] 3.500 [get_ports {Dout[3]}]
set_output_delay -add_delay -min -clock [get_clocks {ext2_clk}] 0.500 [get_ports {Dout[3]}]
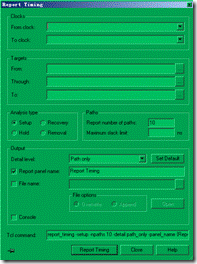
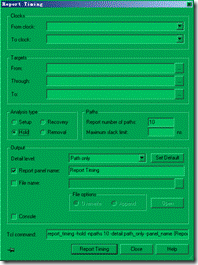
图5.6.7 setup与hold时序分析。
然后我们就可以开始分析时序了 ... 双击 Report Timing，选择 setup与hold分析，其他放空，然后点击 report timing 执行，如图5.6.7所示。
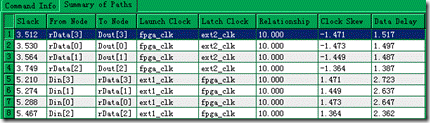
图5.6.8 setup分析结果。
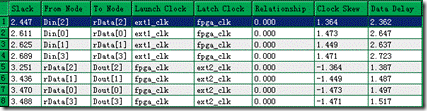
图5.6.9 hold 分析结果。
经过分析以后，我们发现只有8对节点的setup 分析与hold 分析而已 ... 有4对节点是 rData[0:3]~Dout[0:3]，另外4对节点是 Din[0:3]~rData[0:3]。在此，rData是fpga内的寄存器，Din是ic1的寄存器，Dout是ic2的寄存器。从图5.6.8~9中看见的 Clock Skew 或者 Data Delay 基本上是内部模型的延迟结果，与外部模型一丁儿关系也没有 ... 这话何说呢？
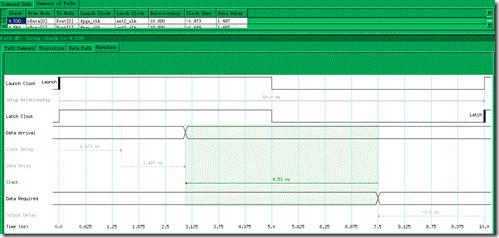
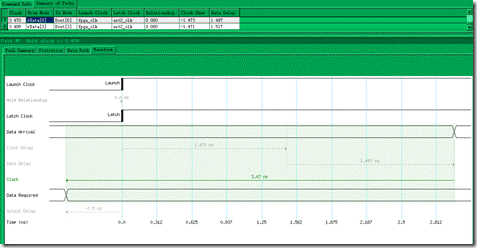
图5.6.10 rData[0]~Dout[0] setup分析的时序图。
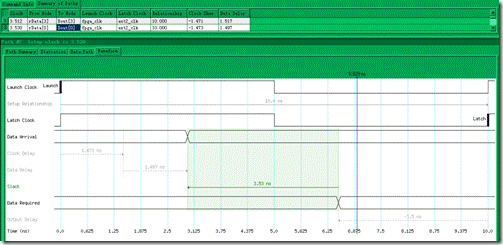
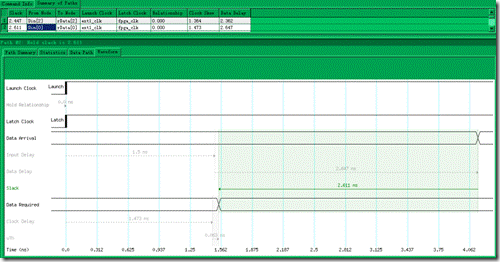
图5.6.11 rDin[0]~rData0] setup分析的时序图。
笔者展开节点 rData[0]~Dout[0]（图5.6.10）还有节点rData[0]~Dout[0]（图5.6.11）的setup分析过程，其中 3.5ns 还有3.5ns就是 set output delay max 与set input delay max 的结果。
图5.6.12 rData[0]~Dout[0] hold分析的时序图。
图5.6.13 rDin[0]~rData0] hold分析的时序图。
接着又展开同样的节点，然后观察该 hold 分析图，如图5.6.12 与图5.6.13所示 ... 其中 0.5ns 与 1.5ns 既是 set output delay min 与 set input delay min 的结果。
在这里，我们得到这样一个结论：
set output delay 与 set input delay 好似一个“外包资料”，首先我们收集各种外部的延迟信息接着包裹在一个“外包资料”里，然后丢给 TimeQuest 。TimeQuest当然晓得某某delay max 是针对建立关系，又某某delay min 是针对保持关系。TimeQuest 在分析内部的 setup 与 hold 时序时顺便参考一下“外包资料”的信息 ... 就这样TimeQuest就可以独立分开外部延迟信息与内部延迟信息。
总结：
第五章终于写完了，这一章的实验数量不但少，而且约束命令的出现也不多，不过内容都是深入理解TimeQuest的要点。这个章节我们先了解网表，事实上网表也有极端与好之分，越是极端保险余量越大，可是性能限制却越大，结果越偏离实际的信息；换之，越是好保险余量越小，性能限制也越小，结果越接近实际的信息。默认下TimeQuest是一位极端的生存者，不过也可以手动要它成为乐天的屁民。
此外，笔者也稍微谈论一下 TimeQuest的迷信，亦即Fmax。笔者初学 TimeQuest的时候，同样也认为 Fmax 是时序分析的重要标准，后来才知道 Fmax 是指某个“最差劲节点”的最高频率。Fmax这东西不是越高越好，就像驾驶跑车那样，就算哪天死了也不会冲到最高速 ... 所以说，够用就好。提升Fmax 有许多方法，除了选择较好的网表以外，还可以设置编译器的选项，当然最根本还是Verilog本身。Fmax也可以是网表质量关系性能限制的评估值。
但是这章让笔者最着重的内容 ... 亦即TimeQuest用非常巧妙的手段将外部信息包裹为“外部资料”，这外部资料有标志性的 max 与 min，而 max是针对建立关系，min则是针对保持关系。外部资料是由以下公式（手段）将外部延迟信息包裹而成：
input max = <ext2fpga delay max> - < destination reg clk delay - source reg clk delay > + ext_Tco
= <ext2fpga delay max> - < clock skew > + ext_Tco
input min = < fpga2ext delay min > - < destination reg clk delay - source reg clk delay > + ext_Tco
= <fpga2ext delay min> - < clock skew > + ext_Tco（或者 ext_minTco）
output max = <fpga2ext delay max> - < destination reg clk delay - source reg clk delay > + ext_Tsu
= <fpga2ext delay max> - < clock skew > + ext_Tsu
output min = < fpga2ext delay min > - < destination reg clk delay - source reg clk delay > - ext_Th
= <fpga2ext delay min> - < clock skew > - ext_Th
对笔者而言，最辛苦的差事就是推导以上的公式 ... 很久以前，笔者在接触TimeQuest不久，它们就出现在手册上。不过一般而言，绝对不会有人犯贱到折腾自己去推导它们。但直觉告诉笔者，推导公式可以让自己更了解 TimeQuest ... 就这样，笔者一度跌进学习的死胡同，然后灰心离开，学习进度从此就定格在哪里。
当《整合篇》完成，时间大约是一年后 ... 笔者再次打开当时的草稿，然后继续思考，不出几天的时间，许多东西就那样自然而然的理解起来 ... 推导整套公式的关键自然是那个不起眼的建立关系与保持关系。心想真妙，建立时间与保持时间既然与建立关系与保持关系有如此微妙的关系，这就是第五章的重点内容。
posted on 2013-12-02 17:39 ALINX官方博客 阅读(2768) 评论(1) 编辑 收藏 举报
