[Matlab]双线性变换法设计数字带通滤波器
测试代码:
%%****bin_bp.m*******************%%
%% 使用双线性变换法设计带通滤波器
%% 2018年6月13日 16:30:34
%% author:Alimy
close all;
clear;
clc;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%代码正文
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%给定数字滤波器指标
f_sl = 150 ; %阻带下限频率(Hz)
f_1 = 200 ; %通带下限频率(Hz)
f_3 = 500 ; %通带上限频率(Hz)
f_sh = 600 ; %阻带上限频率(Hz)
R_p = 0.5 ; %通带允许的最大衰减
R_s = 40 ; %阻带允许的最小衰减
f_s = 2000 ; %采样频率
T_s = 1 / f_s ; %采样间隔
%1.将数字带通滤波器的频率参数变换为归一化的数字角频率参数
omega_sl = 2 * pi * f_sl / f_s; %阻带下限频率
omega_1 = 2 * pi * f_1 / f_s; %通带下限频率
omgea_3 = 2 * pi * f_3 / f_s; %通带上限频率
omega_sh = 2 * pi * f_sh / f_s; %阻带上限频率
%2.预畸变处理,将归一化数字角频率参数变换成模拟带通滤波器的角频率参数
C = 2*f_s ;
Omega_sl = C * tan( omega_sl / 2 );
Omega_1 = C * tan( omega_1 / 2 );
Omega_3 = C * tan( omgea_3 / 2 );
Omega_sh = C * tan( omega_sh / 2 );
%3.对模拟带通滤波器的角频率参数做归一化处理
Omega_BW = Omega_3 - Omega_1;
eta_sl = Omega_sl / Omega_BW;
eta_1 = Omega_1 / Omega_BW;
eta_3 = Omega_3 / Omega_BW;
eta_sh = Omega_sh / Omega_BW;
%4.设计归一化模拟滤波器,得到归一化模拟带通滤波器的转移函数
Omega_p = [ Omega_1 , Omega_3 ];
Omega_s = [ Omega_sl , Omega_sh ];
[ N , Wn ] = buttord( Omega_p , Omega_s , R_p , R_s , 's' ); %选择模拟巴特沃斯滤波器的最小阶数
[ Bs, As ] = butter(N,Wn,'s');
%5.利用模拟带通滤波器的转移函数确定IIR数字滤波器的转移函数
[ bz , az ] = bilinear(Bs,As,f_s);
figure(1);
freqz(bz,az);
title('带通滤波器幅度谱和相位谱特性');
%滤波效果测试
N = 1000;
t = [ 0 : N - 1 ] * T_s ;
f1 = 50;
f2 = 100;
f3 = 300;
x1 = 2*1*sin( 2 * pi * f1 * t );
x2 = 2*2*sin( 2 * pi * f2 * t );
x3 = 2*1*sin( 2 * pi * f3 * t );
x = x1 + x2 + x3;
fft_x = fft( x );
X_mag = fftshift( abs ( fft_x ) ) / N ;
X_ang = fftshift( angle ( fft_x ) );
delta_f = f_s/N;
f = ( -N / 2 : N / 2 - 1 )*delta_f;
figure(2);
subplot(3,1,1);
plot(t,x);
title('原信号时域波形');
xlabel('t(s)');
subplot(3,1,2);
plot( f , X_mag );
title('原信号幅度谱');
xlabel('f(hz)');
subplot(3,1,3);
plot( f , X_ang );
title('原信号相位谱');
xlabel('f(hz)');
%滤波
lp_x = filter( bz , az , x );
lp_fft_x = fft( lp_x );
lp_X_mag = fftshift( abs ( lp_fft_x ) ) / N ;
lp_X_ang = fftshift( angle ( lp_fft_x ) );
figure(3);
subplot(3,1,1);
plot(t,lp_x);
title('滤波后信号时域波形');
xlabel('t(s)');
subplot(3,1,2);
plot( f , lp_X_mag );
title('滤波后信号幅度谱');
xlabel('f(hz)');
subplot(3,1,3);
plot( f , lp_X_ang );
title('滤波后信号相位谱');
xlabel('f(hz)');
效果:
滤波器特性:

待滤波的信号:
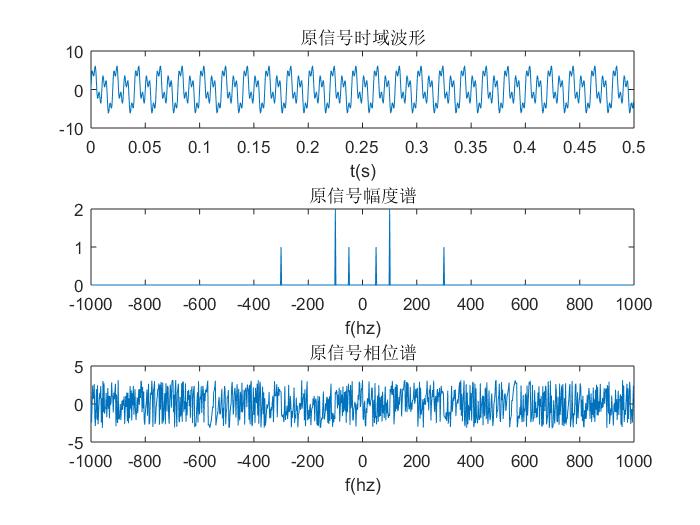
滤波后的信号:
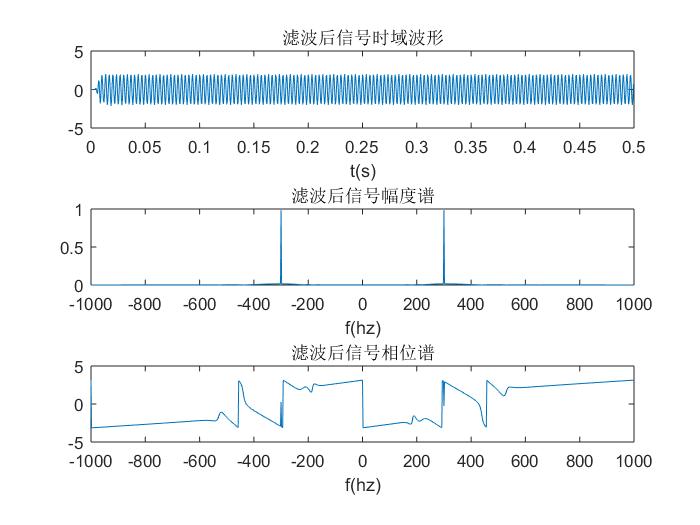
~不再更新,都不让我写公式,博客园太拉胯了




