六边形具有“完全充填”和“最具效率”的双重优势，同时亦遵循着自然界最普遍的原理 - 最小作用量原理。游戏中使用六向网格结构比传统四边形网格结构更具立体层次感，且比基于四边八向地形更能体现游戏的公平性，因此其构建的地图最贴近真实世界 - 地理路网拓扑系统
上一节给大家讲解了如何在四边形单元格基础上构建SLG地图场景，并实现移动、战斗的基础框架；热爱SLG的朋友一定非常清楚，绝大多数的SLG游戏地形单元格都可归为四类：四边四向、四边八向和四边六向、六边六向：
粗看，六边六向是其中构建最复杂的地形，它的称谓很多，比如六面网格、六边网格、晶体网格、蜂窝网格等等，不管叫什么，它总能给我们一种严谨而完美的直观印象。这种奇妙的感觉缘何而来？雪花、分子、螺帽、蜂巢、球网、芯片……在现实生活中，它的身影似乎无处不在。
困惑再一次升级：自然界为何偏偏热衷于复杂？网上的答复让人摸不着头脑，有朋友说六边形结构最省材，有的则说六边形结构最稳定，那难道三角形就不稳定了吗？有的朋友则又说，六边形最牢固且能耗最低，林林种种……
于是迫在眉睫的证据让我阅穿百页搜索，一篇《“天人合一”在六边形里》使我茅塞顿开：
基于空间填充原理：在一个平面中，只有正三角形、正四边形、正六边形三种图形可以完全填满平面，即不互相重叠，也不留下空隙。但是在这三种图形中，如果同样的周长，正六边形的面积最大。也就是说，六边形具有“完全填充”和“最具效率”的双重优势。同时亦遵循着自然界最普遍原理 - 最小作用量原理。
相当给力！
不过，高兴似乎还早了些，Hold住。难道所有的SLG游戏开发者仅仅都因为以上原因而在设计之初选择六边形单元格吗？毫无疑问，非也。游戏，若过分掺杂着教条主义则必将与娱乐背道而驰。要回答这个问题我们还得追溯到SLG游戏的发展史：
SLG游戏类型是最古老的游戏类型之一，其逻辑AI的复杂性也是所有游戏中最高的。在我的印象中，基于六向的SLG游戏最早见于红白机上的《大战略》：
游戏中采用了中庸的四边六向单元格，这样的地图布局起来比六边形构造更简单，但效果却一摸一样。日本厂商不乏类似的SLG大作，比如《火焰纹章 贝里克物语》采用的便这种形式的地形布局：
当然，市面上六向的SLG游戏大多还是采用正统的六边形单元格，比如经典的《天使帝国》和《文明》：
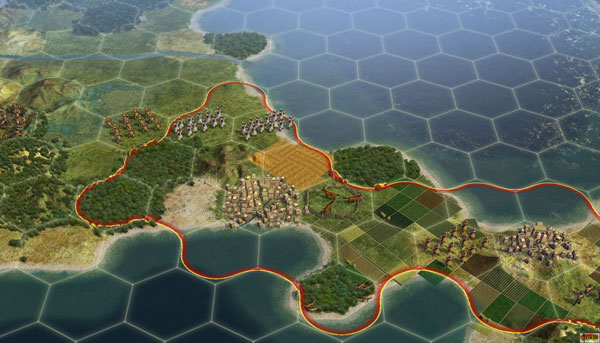
到此，我们将以上四部作品与其他采用四边形单元格的SLG游戏相比较便会发现，基于四边形网格的地图具有局限性，从每个单元格的中心到相邻单元格的中心距离不尽相等,沿纵、横方向上相同,但不同于对角线方向上的距离，即对角线移动比直线移动更快，战略上讲这是非常不公平的；而使用六边形网格地图，其放射对称性原理（单元格中心到所有方向上的相邻单元格中心点的距离均相等）使得游戏更加真实与严谨，此类游戏尤其能体现单位与临接单位之间的绝对公平的相互作用关系。
综合以上分析得出：正六边形单元格是最饱满，且边、角交汇最省的单元格，加上前文所述完全填充且最具效率的双重优势，游戏中使用六向网格结构比传统四边形网格结构更具立体层次感，且比基于四边八向地形更能体现游戏的公平性，因此其构建的地图最贴近真实世界 - 地理路网拓扑系统。
云开见日，有了以上的理论依据，接下来我们便可将真实世界的地理路网映射到游戏中，抽象成基于六边形蜂窝拓扑结构的战略地图：
开始动手吧，打开上一节的Silverlight源码，我们首先要做的就是修改将游戏坐标转换成窗口像素位置的方法(GetPositionFromCoordinate())，这个算法怎么改？似乎还找不着头绪。按照上图布局，我们不妨先做个例枚举，然后通过分析找出其中规律所在。
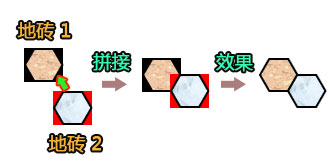
不难看出，虽然每个单元格都拥有六方向，但它们的坐标同样基于二维的X,Y构成，大体看来，Y坐标是连续的，X坐标则是规律起伏的。接下来我们进一步明确，六边形地砖的铺设(拼接)是以左上角最大宽、高作处作为起点:
假设(0,0)单元格的窗口像素位置为(0,0)，那么(0,1)、(0,2)、(1,0)、(1,1)、(1,2)、(2,0)、(2,1)、(2,2)的像素坐标分别是多少？？
如上图，坐标为(0,0)的六边形单元格，其铺设位置起点为O点；坐标为(1,0)的六边形单元格，其铺设位置为M点；而坐标为(0,1)的六边形单元格，其铺设位置为N点，以此类推。于是，我们要分别得到O、M、N的像素位置，则必须知道正六边形的边长以及a、b的长度值：
假设正六边形地砖的边长为L，根据三角形内角和为180度，则六边形内角和为720度，那么正六边形每个角为120度，于是可以得到b与L的夹角为30度。根据三角函数公式可知L、a、b之间的转换公式如下：
a = L * Sin 30°
b = L * Cos30°
同时，我们分别对(0,0)至(2,2)这九个单元格进行枚举，会发现如下规律：
坐标(0,0) 对应的窗口像素位置为(0,0)
坐标(0,1) 对应的窗口像素位置为(0,2b)
坐标(0,2) 对应的窗口像素位置为(0,4b)
……
坐标(1,0) 对应的窗口像素位置为(a+L,b)
坐标(1,1) 对应的窗口像素位置为(a+L,2b+b)
坐标(1,2) 对应的窗口像素位置为(a+L,4b+b)
……
坐标(2,0) 对应的窗口像素位置为(2*(a+L),0)
坐标(2,1) 对应的窗口像素位置为(2*(a+L),2b)
坐标(2,2) 对应的窗口像素位置为(2*(a+L),4b)
……
依次类推
是不是开始有些激动了？其实重点就在于当坐标X为奇数时，Y多加一个b值。假如坐标为(X,Y)的六边形单元格，其所对应的窗口像素位置为(A,B)，则A=X*L*(1+Sin30)，B=(Y*2+X%2)*L*Cos30
最后转换成Silverlight编程语言，GetPositionFromCoordinate()方法修改如下：
/// 获取窗口Canvas中的位置Position(通过空间坐标系中的坐标Coordinate换算而来)
/// </summary>
public Point GetPositionFromCoordinate(Point p) {
double radian30 = 30 * Math.PI / 180;
double x = p.X * GridSide * (1 + Math.Sin(radian30));
double y = (p.Y * 2 + p.X % 2) * GridSide * Math.Cos(radian30);
return TileType == TileTypes.Flat ? new Point(x, y) : new Point(y, x);
}
如此大的周折也仅仅是完成了蜂窝拓扑结构地砖铺设而已，下一个任务便是修改角色的移动范围算法；有了前面详尽的分析，这道工序相对简单了很多。基于上一节四叉树遍历算法基础上我们进行如下修改：
/// 六方遍历扫描
/// </summary>
Dictionary<Point2D, int> RangeScan(Dictionary<Point2D, int> tempList, Dictionary<Point2D, int> rangeList, int moveLimit) {
Dictionary<Point2D, int> result = new Dictionary<Point2D, int>();
for (int i = 0; i < tempList.Count; i++) {
KeyValuePair<Point2D, int> kvp = tempList.ElementAt(i);
DirectionScan(new Point2D(kvp.Key.X, kvp.Key.Y - 1), kvp.Value, result, rangeList, moveLimit);
DirectionScan(new Point2D(kvp.Key.X + 1, kvp.Key.Y), kvp.Value, result, rangeList, moveLimit);
DirectionScan(new Point2D(kvp.Key.X, kvp.Key.Y + 1), kvp.Value, result, rangeList, moveLimit);
DirectionScan(new Point2D(kvp.Key.X - 1, kvp.Key.Y), kvp.Value, result, rangeList, moveLimit);
if (kvp.Key.X % 2 == 0) {
DirectionScan(new Point2D(kvp.Key.X + 1, kvp.Key.Y - 1), kvp.Value, result, rangeList, moveLimit);
DirectionScan(new Point2D(kvp.Key.X - 1, kvp.Key.Y - 1), kvp.Value, result, rangeList, moveLimit);
} else {
DirectionScan(new Point2D(kvp.Key.X - 1, kvp.Key.Y + 1), kvp.Value, result, rangeList, moveLimit);
DirectionScan(new Point2D(kvp.Key.X + 1, kvp.Key.Y + 1), kvp.Value, result, rangeList, moveLimit);
}
}
return result;
}
完了吗？还没，最关键的时刻到了，上一节的A*算法只能满足四向或八向寻路，如何实现六向寻路A*算法？重写一个？NO，其实我们只需对方向遍历模块进行修改，使之变成六向检索，且每个单元格的移动消耗设置一致即可：
以A*算法中的PathFinderFast为例，修为内容如下：
PathFinderFast修改部分
mDirection = new sbyte[6, 2] { { 0, -1 }, { 1, 0 }, { 0, 1 }, { -1, 0 }, { 1, -1 }, { -1, -1 } };
} else {
mDirection = new sbyte[6, 2] { { 0, -1 }, { 1, 0 }, { 0, 1 }, { -1, 0 }, { -1, 1 }, { 1, 1 } };
}
for (int i=0; i< 6; i++)
{
mNewLocationX = (ushort) (mLocationX + mDirection[i,0]);
mNewLocationY = (ushort) (mLocationY + mDirection[i,1]);
......
}
终于大功告成。当然，SLG中蜂窝结构地图亦并非是十全十美的，其在移动及战斗(范围)方面的灵活性与趣味性表现相对较差。
比如，四边形地图可轻松实现十字斩，那么六边形地图呢？
同时，由于X坐标方向高低起伏，角色X方向的移动会显得特别别扭：
当然，我们是可以通过一些人性化设置来规避这些尴尬的。最经典的以《英雄无敌3》为例，计算好寻路后只需执行起点与终点之间的直线移动即可，而范围攻击则可使用六边形外接圆形式巧取而代之，等等。
非常值得一提的是，蜂窝拓扑结构基础单元格常用的除了平型(比如前文提到的《天使帝国》)，还有尖形(例如前文提到的《文明》)：
两者的互换只需对单元格素材进行30度旋转，同时在坐标转换时将X与Y的位置互换即可：
终于完工了。
这是一款基于Silverlight的SLG游戏引擎的一部分，在线演示Demo 如下(点击下载该Demo源码)：
手记小结：蜂窝拓扑结构在计算机网络概述中有详细讲解，其应用领域亦非常广泛；除游戏外，蜂窝拓扑结构在无线通信网络技术、图像显示，地理信息布局等领域都极具优势，非常值得大家深度研究。
一则令人兴奋的消息：微软应用商店(Marketplace)已向中国开发人员开放，同时种种迹象证实了微软正在研发下一代XBOX，是的，微软正将使用Silverlight开发新一代XBOX程序！有限的生命只需精通最完美的技术足以，或许我们是时候丢掉垃圾，对不需要的技术说“不”了。Let,s focus on Silverlight！Come on
