内部排序->选择排序->堆排序
文字描述
堆排序中,待排序数据同样可以用完全二叉树表示, 完全二叉树的所有非终端结点的值均不大于(或小于)其左、右孩子结点的值。由此,若序列{k1, k2, …, kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
若在输出堆顶的最小值之后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素中的次小值。如此反复执行,便能得到一个有序序列,这个过程称之为堆排序。
由此,实现堆排序需要解决两个问题:(1)如何由一个无序序列建成一个堆?(2)如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
先讨论第(2)个问题,假设有个最大堆(堆顶元素为堆的最大值)输出堆顶元素之后, 以堆中最后一个元素代替之,此时根结点的左、右子树均为堆,则仅需自上至下进行调整即可。称这个自堆顶至叶子的调整过程为“筛选”。
再讨论第(1)个问题,由一个无序序列建成堆的过程就是一个反复”筛选”的过程。若将此序列看成一个完全二叉树,则最后一个非终端结点是第[n/2]个元素,由此“筛选”只需从第[n/2]个元素开始。
示意图
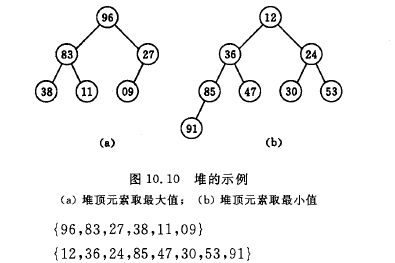
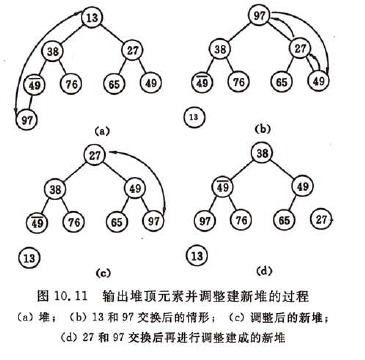
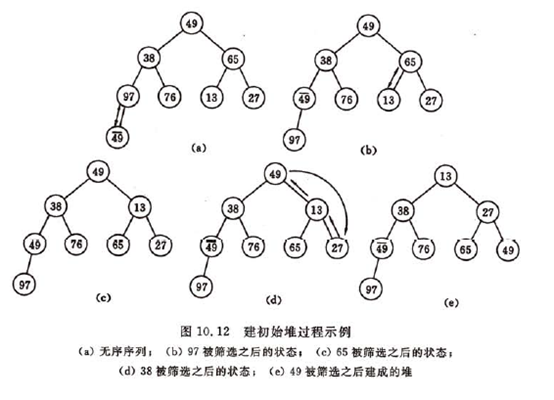
算法分析
堆排序在树形选择排序上进行了改进, 和树形选择排序比, 堆排序可以减少辅助空间, 避免和”最大值”的冗余比较等优点.
堆排序在最坏情况下,其时间复杂度也为nlogn。相对于快速排序来说,这是堆排序的最大优点(快速排序最坏情况下时间复杂度为n*n, 但平均性能为nlogn)。
堆排序只需一个记录大小的辅助空间供交换用。
堆排序是一种不稳定的排序方法。
另外,堆排序方法对记录数较少的文件并不提倡使用, 但是对n较大的文件还是很有效的,因为其运行时间主要耗费在建立初始堆和调整新堆时的反复“筛选”上。
代码实现

1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <math.h> 4 /* 5 * double log2(double x); 以2为底的对数 6 * double ceil(double x); 取上整 7 * double floor(double x); 取下整 8 * double fabs(double x); 取绝对值 9 */ 10 11 #define DEBUG 12 13 #define EQ(a, b) ((a) == (b)) 14 #define LT(a, b) ((a) < (b)) 15 #define LQ(a, b) ((a) <= (b)) 16 17 #define MAXSIZE 100 18 #define INF 1000000 19 typedef int KeyType; 20 typedef char InfoType; 21 typedef struct{ 22 KeyType key; 23 InfoType otherinfo; 24 }RedType; 25 26 typedef struct{ 27 RedType r[MAXSIZE+1]; 28 int length; 29 }SqList; 30 31 void PrintList(SqList L){ 32 int i = 0; 33 printf("下标值:"); 34 for(i=0; i<=L.length; i++){ 35 printf("[%d] ", i); 36 } 37 printf("\n关键字:"); 38 for(i=0; i<=L.length; i++){ 39 if(EQ(L.r[i].key, INF)){ 40 printf(" %-3c", '-'); 41 }else{ 42 printf(" %-3d", L.r[i].key); 43 } 44 } 45 printf("\n其他值:"); 46 for(i=0; i<=L.length; i++){ 47 printf(" %-3c", L.r[i].otherinfo); 48 } 49 printf("\n\n"); 50 return ; 51 } 52 53 //堆采用顺序存储表示 54 typedef SqList HeapType; 55 56 /* 57 *已知H->r[s,...,m]中记录的关键字除H->r[s].key之外均满足的定义 58 *本汉书调整H-r[s]的关键字,使H->r[s,...,m]成为一个大顶堆(对其中 59 *记录的关键字而言) 60 */ 61 void HeapAdjust(HeapType *H, int s, int m) 62 { 63 RedType rc = H->r[s]; 64 int j = 0; 65 //沿key较大的孩子结点向下筛选 66 for(j=2*s; j<=m; j*=2){ 67 //j为key较大的纪录的下标 68 if(j<m && LT(H->r[j].key, H->r[j+1].key)) 69 j+=1; 70 //rc应该插入位置s上 71 if(!LT(rc.key, H->r[j].key)) 72 break; 73 H->r[s] = H->r[j]; 74 s = j; 75 } 76 //插入 77 H->r[s] = rc; 78 } 79 80 /* 81 * 对顺序表H进行堆排序 82 */ 83 void HeapSort(HeapType *H) 84 { 85 int i = 0; 86 //把H->r[1,...,H->length]建成大顶堆 87 for(i=H->length/2; i>=1; i--){ 88 HeapAdjust(H, i, H->length); 89 } 90 #ifdef DEBUG 91 printf("由一个无序序列建成一个初始大顶堆:\n"); 92 PrintList(*H); 93 #endif 94 RedType tmp; 95 for(i=H->length; i>1; i--){ 96 //将堆顶记录和当前未经排序子序列H->r[1,...,i]中最后一个记录相互交换 97 tmp = H->r[1]; 98 H->r[1] = H->r[i]; 99 H->r[i] = tmp; 100 //将H->r[1,...,i-1]重新调整为大顶堆 101 HeapAdjust(H, 1, i-1); 102 #ifdef DEBUG 103 printf("调整1至%d的元素,使其成为大顶堆:\n", i-1); 104 PrintList(*H); 105 #endif 106 } 107 } 108 109 int main(int argc, char *argv[]) 110 { 111 if(argc < 2){ 112 return -1; 113 } 114 HeapType H; 115 int i = 0; 116 for(i=1; i<argc; i++){ 117 if(i>MAXSIZE) 118 break; 119 H.r[i].key = atoi(argv[i]); 120 H.r[i].otherinfo = 'a'+i-1; 121 } 122 H.length = (i-1); 123 H.r[0].key = 0; 124 H.r[0].otherinfo = '0'; 125 printf("输入数据:\n"); 126 PrintList(H); 127 //对顺序表H作堆排序 128 HeapSort(&H); 129 return 0; 130 }
运行
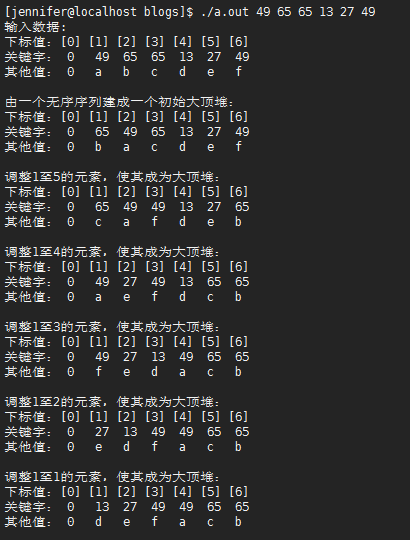
posted on 2018-07-27 18:28 LiveWithACat 阅读(314) 评论(0) 编辑 收藏 举报



