决策树分类算法及python代码实现案例
决策树分类算法
1、概述
决策树（decision tree）——是一种被广泛使用的分类算法。
相比贝叶斯算法，决策树的优势在于构造过程不需要任何领域知识或参数设置
在实际应用中，对于探测式的知识发现，决策树更加适用。
2、算法思想
通俗来说，决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：
女儿：多大年纪了？
母亲：26。
女儿：长的帅不帅？
母亲：挺帅的。
女儿：收入高不？
母亲：不算很高，中等情况。
女儿：是公务员不？
母亲：是，在税务局上班呢。
女儿：那好，我去见见。
这个女孩的决策过程就是典型的分类树决策。
实质：通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见
假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑
上图完整表达了这个女孩决定是否见一个约会对象的策略，其中：
◊绿色节点表示判断条件
◊橙色节点表示决策结果
◊箭头表示在一个判断条件在不同情况下的决策路径
图中红色箭头表示了上面例子中女孩的决策过程。
这幅图基本可以算是一颗决策树，说它“基本可以算”是因为图中的判定条件没有量化，如收入高中低等等，还不能算是严格意义上的决策树，如果将所有条件量化，则就变成真正的决策树了。
决策树分类算法的关键就是根据“先验数据”构造一棵最佳的决策树，用以预测未知数据的类别
决策树：是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。
3、决策树构造
假如有以下判断苹果好坏的数据样本：
|
样本 红 大 好苹果 0 1 1 1 1 1 0 1 2 0 1 0 3 0 0 0 |
样本中有2个属性，A0表示是否红苹果。A1表示是否大苹果。假如要根据这个数据样本构建一棵自动判断苹果好坏的决策树。
由于本例中的数据只有2个属性，因此，我们可以穷举所有可能构造出来的决策树，就2棵，如下图所示：
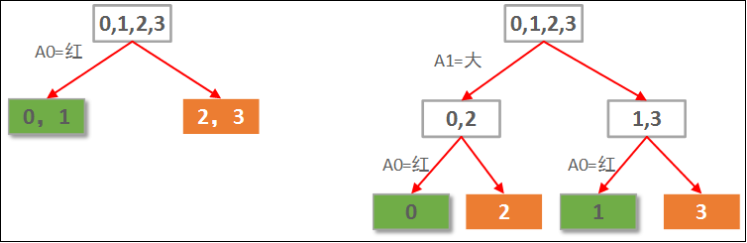
显然左边先使用A0（红色）做划分依据的决策树要优于右边用A1（大小）做划分依据的决策树。
当然这是直觉的认知。而直觉显然不适合转化成程序的实现，所以需要有一种定量的考察来评价这两棵树的性能好坏。
决策树的评价所用的定量考察方法为计算每种划分情况的信息熵增益：
如果经过某个选定的属性进行数据划分后的信息熵下降最多，则这个划分属性是最优选择
属性划分选择（即构造决策树）的依据：
简单来说，熵就是“无序，混乱”的程度。
通过计算来理解：
1、原始样本数据的熵：
样例总数：4
好苹果：2
坏苹果：2
熵： -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1
信息熵为1表示当前处于最混乱，最无序的状态。
2、两颗决策树的划分结果熵增益计算
树1先选A0作划分，各子节点信息熵计算如下：
0，1叶子节点有2个正例，0个负例。信息熵为：e1 = -(2/2 * log(2/2) + 0/2 * log(0/2)) = 0。
2，3叶子节点有0个正例，2个负例。信息熵为：e2 = -(0/2 * log(0/2) + 2/2 * log(2/2)) = 0。
因此选择A0划分后的信息熵为每个子节点的信息熵所占比重的加权和：E = e1*2/4 + e2*2/4 = 0。
选择A0做划分的信息熵增益G（S, A0）=S - E = 1 - 0 = 1.
事实上，决策树叶子节点表示已经都属于相同类别，因此信息熵一定为0。
树2先选A1作划分，各子节点信息熵计算如下：
0，2子节点有1个正例，1个负例。信息熵为：e1 = -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1。
1，3子节点有1个正例，1个负例。信息熵为：e2 = -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1。
因此选择A1划分后的信息熵为每个子节点的信息熵所占比重的加权和：E = e1*2/4 + e2*2/4 = 1。也就是说分了跟没分一样！
选择A1做划分的信息熵增益G（S, A1）=S - E = 1 - 1 = 0.
因此，每次划分之前，我们只需要计算出信息熵增益最大的那种划分即可。
先做A0划分时的信息熵增益为1>先做A1划分时的信息熵增益，所以先做A0划分是最优选择！！！
4、算法指导思想
经过决策属性的划分后，数据的无序度越来越低，也就是信息熵越来越小
5、算法实现
梳理出数据中的属性
比较按照某特定属性划分后的数据的信息熵增益，选择信息熵增益最大的那个属性作为第一划分依据，然后继续选择第二属性，以此类推
