HDU 1400 （POJ 2411 ZOJ 1100）Mondriaan's Dream（DP + 状态压缩）

Mondriaan's Dream

Problem Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways. 



Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare! 

 

Input

The input file contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11. 

 

Output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

 

Sample Input

1 2

1 3

1 4

2 2

2 3

2 4

2 11

4 11

0 0

 

Sample Output

1

0

1

2

3

5

144

51205

 

题目大意：用长为2，宽为1的矩形填充满长为h，宽为w的矩形有多少种方案？

 

分析：

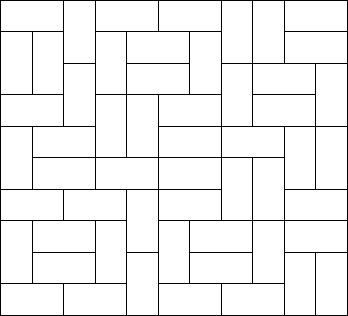
由于长和宽均小于等于11，故每一行均可用一个2进制数表示其状态。我们用1表示竖放的方格，0表示横放的方格。那么样例中各行的状态分别为：

00100001100 

11110011100 

11110011001 

00111001001 

10011000011 

10000001111 

00001001100 

10011100100 

10011100111 

00001000011 

转化为十进制，就是268，1948，1945，457，1219，1039，76，1252，1255，67。

　　用dp(i,j)表示第 i 行状态为 j 时，有多少种排法。那么dp(i,j)应该等于前 i-1 行，状态 k 与 j 相符的排法数的和。状态相符，即在 j 二进制数上为１的位，k 一定也为１。在向下递归时，应该把 k 中和 j 二进制状态中同为１的位置为０，即应该求 dp(i-1,k^j)，原因是当第 i-1 行与第 i 行相接后，二者同为１的地方消掉了，应该当作０处理。

　　所以为了方便，题目描述中那个最大矩阵的第一行就表示为00100001100，第二行就表示为11010010000，这样的话，当上一层j位置为1时，下一层j位置一定为0

当上一层j位置为0时，下一层j位置可以为1，也可以为0,并且当上下都层为0时，零的个数要为偶数，这样上下层的状态相&为0。

　　所以dp(i,j)=sum{dp(i-1,k^j),（k&&j)==0&&judge(k^j)}（judge(k)表示k是有效的行状态，即二进制数状态中连续的０个数为偶数，可先生成存入数组中）。所求答案即为dp(n,0).

　　初始化dp(0,i)=0，dp(0,0)=1。

　　注意结果要用long long或__int64保存，还有要注意位运算的优先级是很低的。

 

代码如下：

 

# include<stdio.h>
__int64 dp[12][1<<12];
int h,w;

bool judge(int s){    //判断状态s是否成立
    int count;
    count = 0;    //s中0的个数
    for(int i=0;i<w; i++){
        if(s & 1){
            if(count & 1)    //1的前面0的个数非偶数，不成立
                return false;
        }
        else
            count ++;
        s >>= 1;
    }
    if(count & 1)    //奇数个0，不成立
        return false;
    else
        return true;
}

int main(){
    int i,j,k;
    while(scanf("%d%d",&h,&w),h+w){
        if((h*w) & 1){        //这种情况下无论如何也不能填满
            printf("0\n");
            continue;
        }
        dp[0][0] = 1;
        for(i=1; i<=h; i++)
            for(j=0; j<(1<<w); j++){
                dp[i][j] = 0;        //初始化
                for(k=0; k<(1<<w); k++)
                    if((j&k)==0 && judge(j^k))
                        dp[i][j] += dp[i-1][k];
            }
        printf("%I64d\n",dp[h][0]);
    }
    return 0;
}