poj3164最小树形图模板题

题目大意：给定一个有向图，根节点已知，求该有向图的最小树形图。最小树形图即有向图的最小生成树，定义为：选择一些边，使得根节点能够到达图中所有的节点，并使得选出的边的边权和最小。

题目算法：朱-刘算法（即由中国人朱永津和刘振宏共同发明的算法）。

算法步骤如下：

1.判断图的连通性，若不连通直接无解，否则一定有解。

2.为除了根节点以外的所有点选择一个权值最小的入边，假设用pre数组记录前驱，f数组记录选择的边长，记所选边权和为temp。

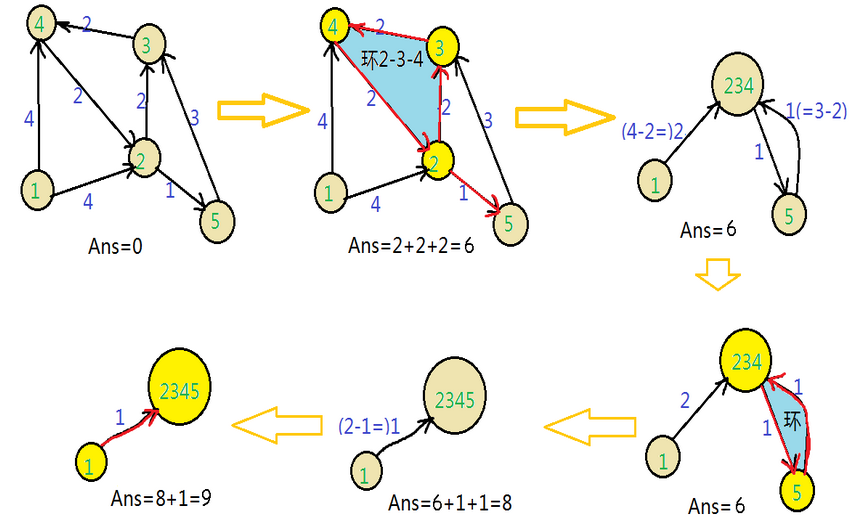
3.（可利用并查集）判断选择的的边是否构成环，若没有则直接ans+=temp并输出ans，若有，则进行下一步操作。

4.对该环实施缩点操作，设该环上有点V1，V2……Vi……Vn，缩成的点为node ，对于所有不在环中的点P进行如下更改：

（1） 点P到node的距离为min{a[p,Vi]-f[Vi]} (a为边集数组)

 （2）点node到p的距离为min{a[Vi,p]}

操作（1）的理解：先假设环上所有边均选上，若下次选择某一条边进入该环，则可以断开进入点与进入点的前驱之间的边，即断开F[进入点]，所以等效为直接把a[p,node]赋值为min{a[p,Vi]-f[Vi]}。

特别提醒：本题有自环，可以提前删掉，因为它没有用。

最后G++double输出lf会wa，改成f就好了，或者用c++提交

#include<map>
#include<set>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<cstdio>
#include<cassert>
#include<iomanip>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define pi acos(-1)
#define ll long long
#define mod 1000000007
#define ls l,m,rt<<1
#define rs m+1,r,rt<<1|1
#pragma comment(linker, "/STACK:1024000000,1024000000")

using namespace std;

const double g=10.0,eps=1e-9;
const int N=100+10,maxn=100000+10,inf=0x3f3f3f;

double x[N],y[N];
int n,m;
int pre[N];
bool vis[N],in[N];
double w[N][N];
double dis(int a,int b)
{
    return sqrt((x[a]-x[b])*(x[a]-x[b])+(y[a]-y[b])*(y[a]-y[b]));
}
void dfs(int u)
{
    vis[u]=1;
    for(int i=1;i<=n;i++)
        if(!vis[i]&&w[u][i]<inf)
           dfs(i);
}
double dirmst(int u)
{
    double ans=0;
    dfs(u);
    for(int i=1;i<=n;i++)
        if(!vis[i])
          return -1;
    memset(vis,0,sizeof vis);
    while(1){
        for(int i=1;i<=n;i++)
        {
            if(i!=u&&!in[i])
            {
                w[i][i]=inf;
                pre[i]=i;
                for(int j=1;j<=n;j++)
                    if(!in[j]&&w[j][i]<w[pre[i]][i])
                        pre[i]=j;
            }
        }
        int i;
        for(i=1;i<=n;i++)
        {
            if(i!=u&&!in[i])
            {
                int j=i,cnt=0;
                while(j!=u&&pre[j]!=i&&cnt<=n)cnt++,j=pre[j];
                if(j==u||cnt>n)continue;
                break;
            }
        }
        if(i>n)
        {
            for(int j=1;j<=n;j++)
                if(j!=u&&!in[j])
                    ans+=w[pre[j]][j];
            return ans;
        }
        int j=i;
        memset(vis,0,sizeof vis);
        do{
            ans+=w[pre[j]][j],j=pre[j],vis[j]=in[j]=1;
        }while(j!=i);
        in[i]=0;
        for(int k=1;k<=n;k++)
            if(vis[k])
               for(int j=1;j<=n;j++)
                  if(!vis[j])
                  {
                      if(w[i][j]>w[k][j])w[i][j]=w[k][j];
                      if(w[j][k]<inf&&w[j][k]-w[pre[k]][k]<w[j][i])
                        w[j][i]=w[j][k]-w[pre[k]][k];
                  }
    }
    return ans;
}
int main()
{
  /*  ios::sync_with_stdio(false);
    cin.tie(0);
    cout<<setiosflags(ios::fixed)<<setprecision(2)<<endl;*/
    while(~scanf("%d%d",&n,&m)){
        for(int i=1;i<=n;i++)
            scanf("%lf%lf",&x[i],&y[i]);
        for(int i=1;i<=n;i++)
        {
            vis[i]=in[i]=0;
            for(int j=1;j<=n;j++)
                w[i][j]=inf;
        }
        while(m--){
            int a,b;
            scanf("%d%d",&a,&b);
            if(a==b)continue;
            w[a][b]=dis(a,b);
        }
      /*  for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
                cout<<w[i][j]<<" ";
            cout<<endl;
        }*/
        double ans=dirmst(1);
        if(ans<0)printf("poor snoopy\n");
        else printf("%.2f\n",ans);
    }
    return 0;
}