C语言程序设计第四次作业——选择结构（2）

（一）改错题
输出三角形的面积和周长，输入三角形的三条边a、b、c，如果能构成一个三角形，输出面积area和周长perimeter（保留2位小数）；否则，输出“These sides do not correspond to a valid triangle”。
输入输出样例1：
　　Enter 3 sides of the triangle: 5 5 3
　　area = 7.15； perimeter = 13.00
输入输出样例2：
　　Enter 3 sides of the triangle: 1 4 1
　　These sides do not correspond to a valid triangle
源程序（有错误的程序）

#include <stdio.h>
#include <math.h>
int main(void)
{
    double a,b,c;
    double area,perimeter,s;

    printf("Enter 3 sides of the triangle: ");
    scanf( "%lf%lf%lf",&a,&b,&c );

    if( a + b > c || b + c > a || a + c > b) 
        s = ( a + b + c ) / 2;
        area = sqrt( s * ( s - a ) * ( s - b ) * ( s - c );
        perimeter = a + b + c;
        printf("area = %.2f; perimeter = %.2f\n",area,perimeter);

    else
        printf("These sides do not correspond to a valid triangle\n");

    return 0;        
}

对源程序进行编译，采用每次修改第一个错误并重新编译的方法，记录每个错误的错误信息、分析错误原因并给出正确的语句。
错误信息1：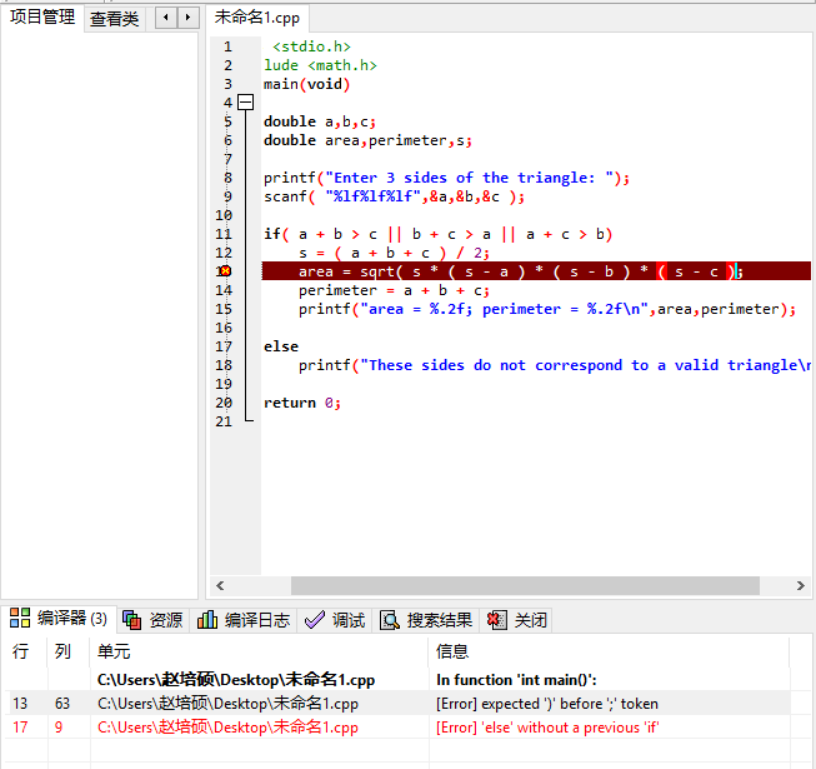
错误原因：第13行的赋值语句中，分号前少加一个后括号。
改正方法：把第13行的赋值语句的分号前加一个后括号。
正确语句：area = sqrt( s * ( s - a ) * ( s - b ) * ( s - c ));
错误信息2：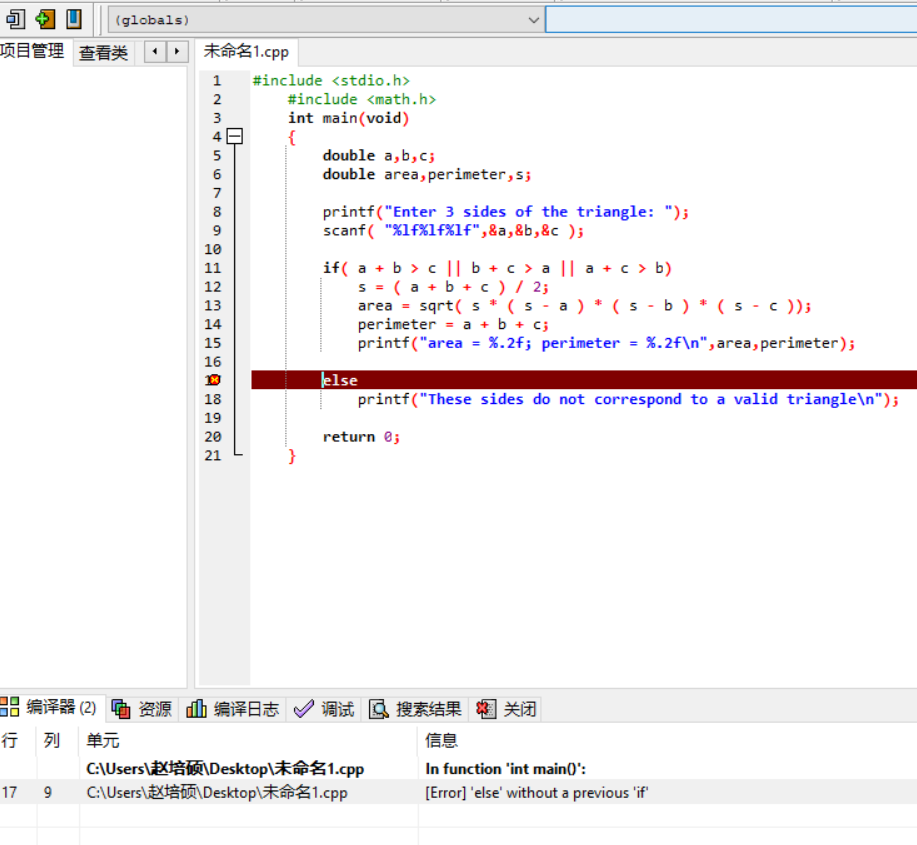
错误原因：if-else语句中的执行语句没有加大括号。
改正方法：把if-else语句中的执行语句加上大括号。
正确语句：

{
    s = ( a + b + c ) / 2;
    area = sqrt( s * ( s - a ) * ( s - b ) * ( s - c ));
    perimeter = a + b + c;
    printf("area = %.2f; perimeter = %.2f\n",area,perimeter);
}

试运行源程序：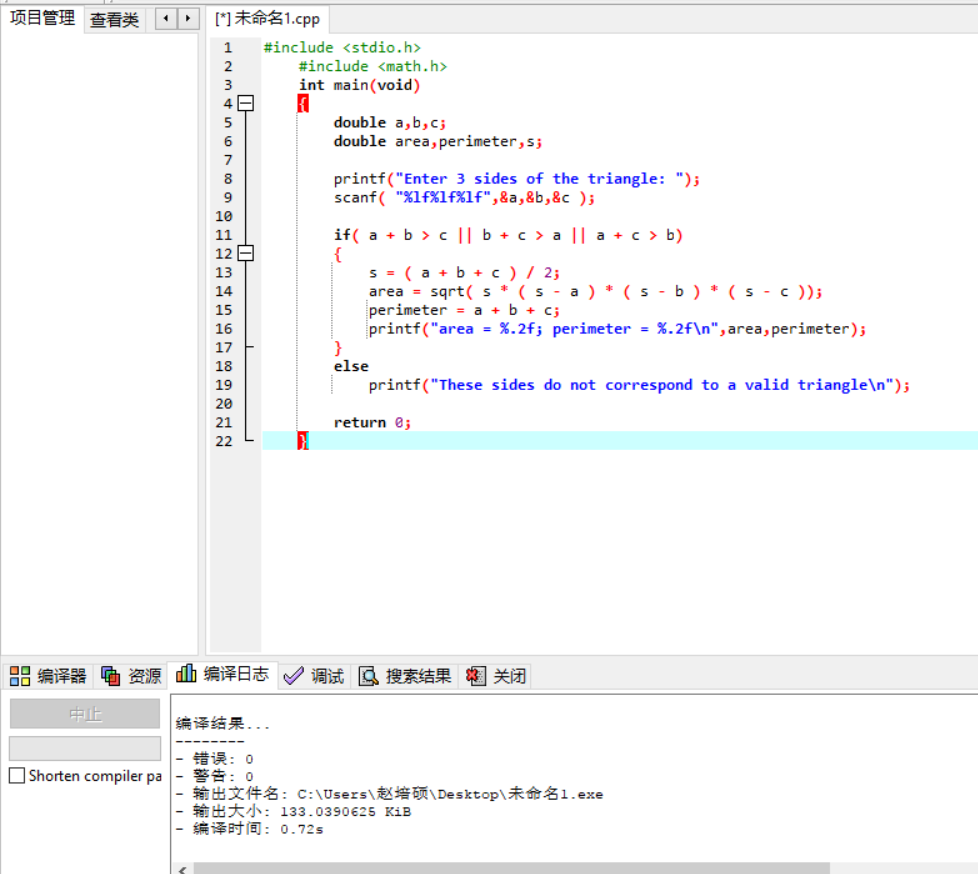
输入样例1，得到：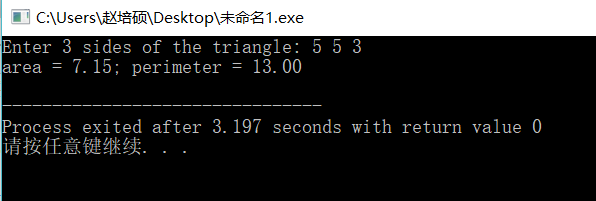
与预期结果相同。
输入样式2，得到：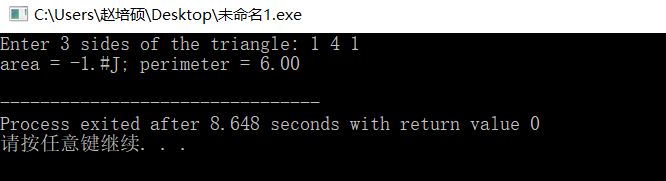
与预期结果不同。

错误信息3：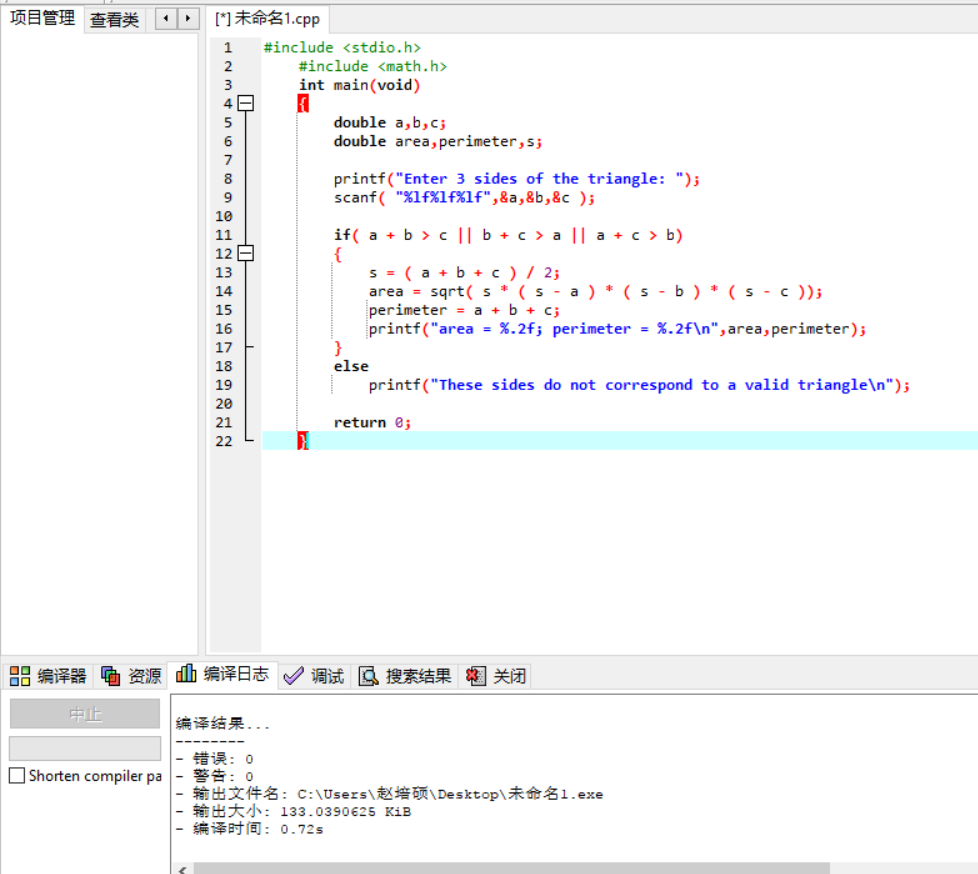
错误原因：第11行的选择语句中，错把 && 写成了 || 。
改正方法：把第11行的选择语句的 && 改为 || 。
正确语句：if( a + b > c && b + c > a && a + c > b)

试运行源程序：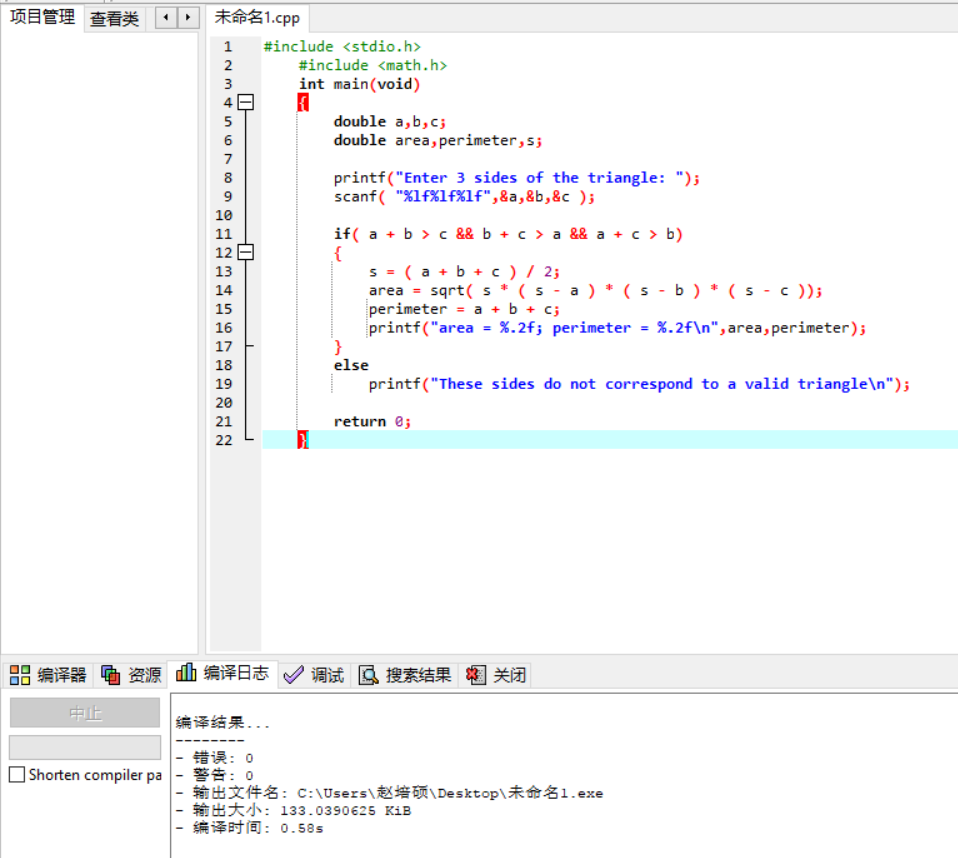
输入样例1，得到：
输入样式2，得到：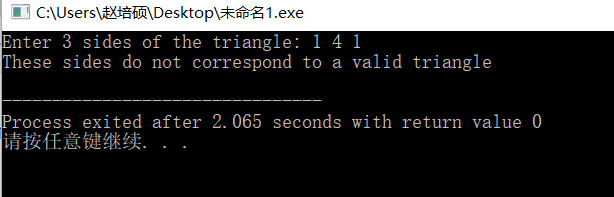
（二）学习总结
1.在编程解决问题的过程中，我们会用到多个if语句，if...else if... 语句以及switch语句，查阅资料，总结一下这三种情况的区别何在，并分别举例加以说明。
（1）三者本质的区别是 if-else语句更适合于对区间（范围）的判断，而switch语句更适合于对离散值的判断
（2）示例
判断65分到85分之间的学生有哪些适合用if-else或多个if语句，因为[65,85]是区间
而判断一个学生的班级是一班、二班还是三班适合用switch语句，因为一班、二班、三班是离散值
（3）扩展
所有的switch语句都可以用if-else或多个if语句来替换（因为if-else语句只需对每个离散值分别做判断即可），而并不是所有的if-else或多个if语句都可以用switch语句来替换（因为区间里值的个数是无限的并且switch所接受的值只能是整型或枚举型，所以不能用case来一一列举)。
（4）对多个if语句和if...else if... 语句进行分析
if — else if是当判断到有一个条件成立时，则后面的else if条件语句就不判断了，这样就节省了程序运行的时间
多个if语句是所有if条件语句都要判断，即使有满足条件的if语句后面的if条件语句也要判断
多个if条件之间是并列关系
参考链接：https://zhidao.baidu.com/question/557831030.html
https://zhidao.baidu.com/question/332651860.html
2.总结
（1）应熟练掌握并熟练运用switch语句，应注意 case 后要打空格。并准确的输入 break 。其格式为：

switch(op)
{
    case '+':
    break；
    case '-':
    break；
    case '*':
    break；
    case '/':
    break；
}

（2）应熟练掌握并熟练运用字符型数据，其包括 putchar函数（字符输出函数）和 getcher函数（字符输入函数）等。
（三）实验总结
1 成绩转换
（1）题目
本题要求编写程序将一个百分制成绩转换为五分制成绩。转换规则：
大于等于90分为A；
小于90且大于等于80为B；
小于80且大于等于70为C；
小于70且大于等于60为D；
小于60为E。
（2）流程图

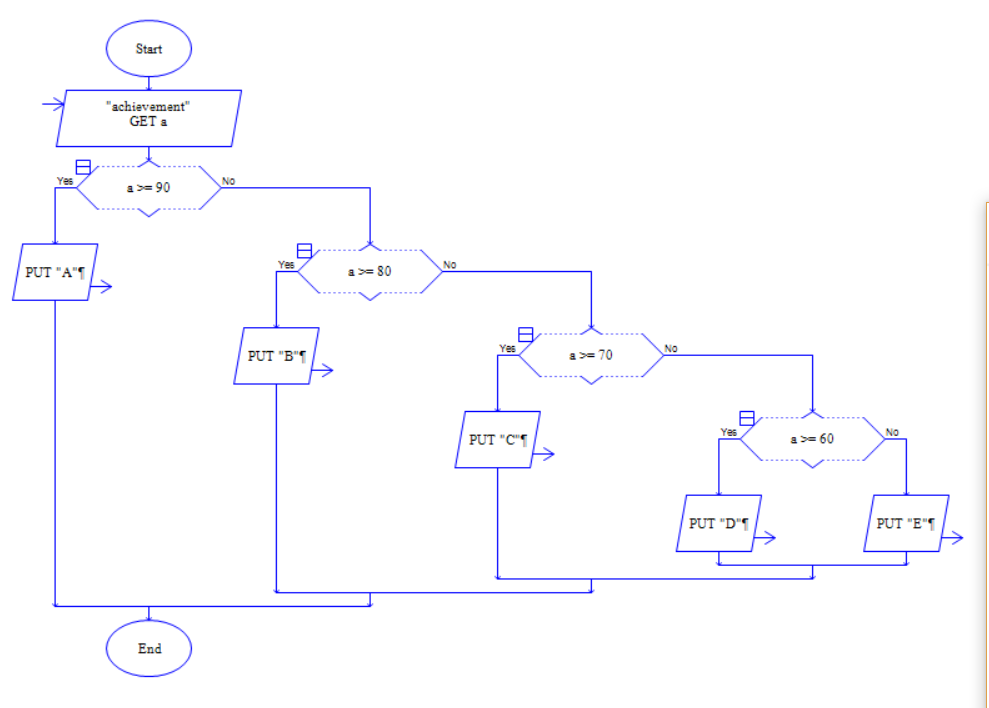
（3）源代码

# include <stdio.h>
int main()
{
int c;

scanf("%d", &c);
switch(c/10)
{
	case 10:
	case 9:printf("A");
	break;
	case 8:printf("B");
	break;
	case 7:printf("C");
	break;
	case 6:printf("D");
	break;
	default :printf("E");
}

return 0;
}

（4）实验分析
问题：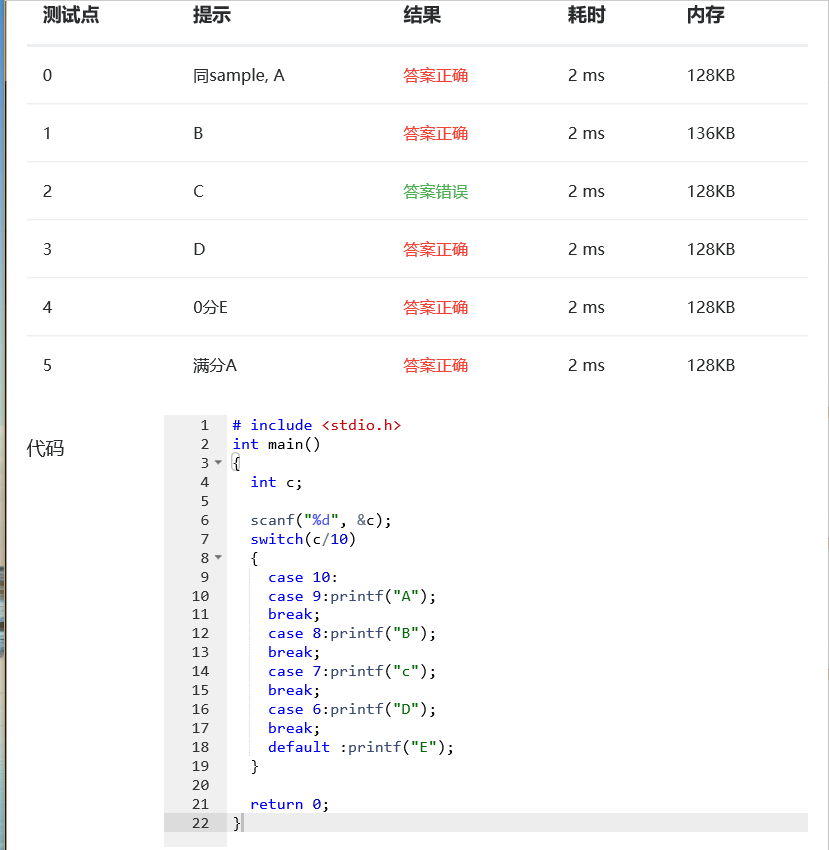
原因：输出C的语句中C小写了。
解决办法：把输出C的语句中的 c 改为 C 。
（5）本题PTA提交列表

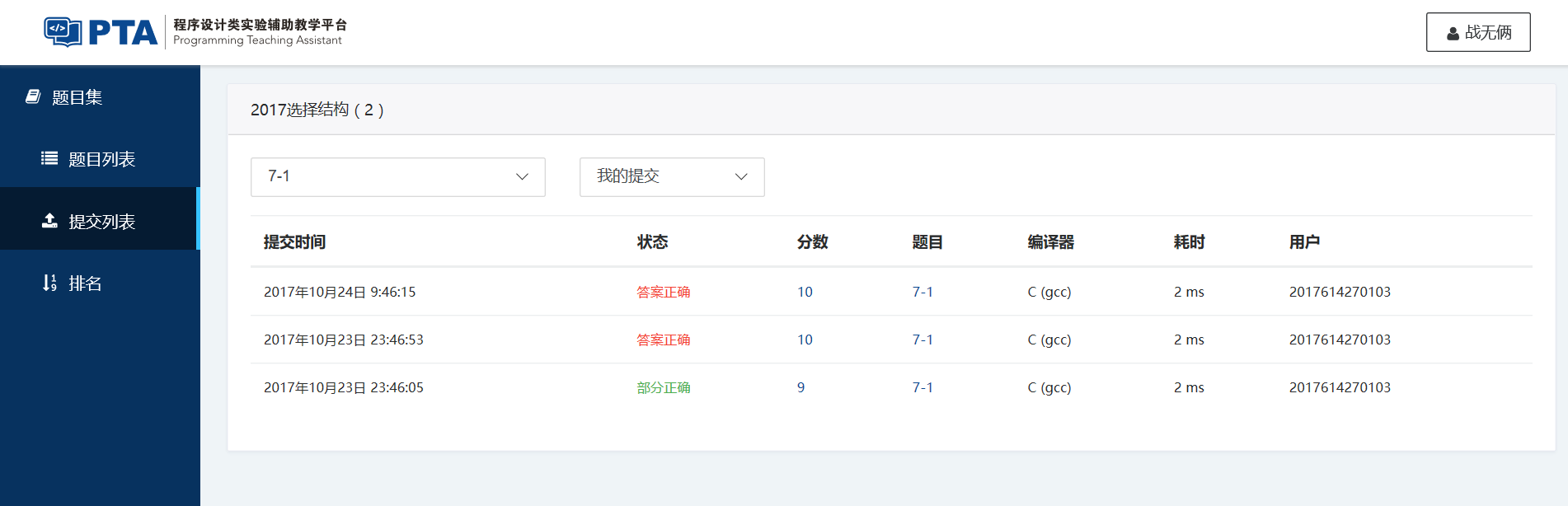
5 三角形判断
（1）题目
给定平面上任意三个点的坐标(x1,y1)、(x2,y2)、(x3,y3)，检验它们能否构成三角形。
（2）流程图

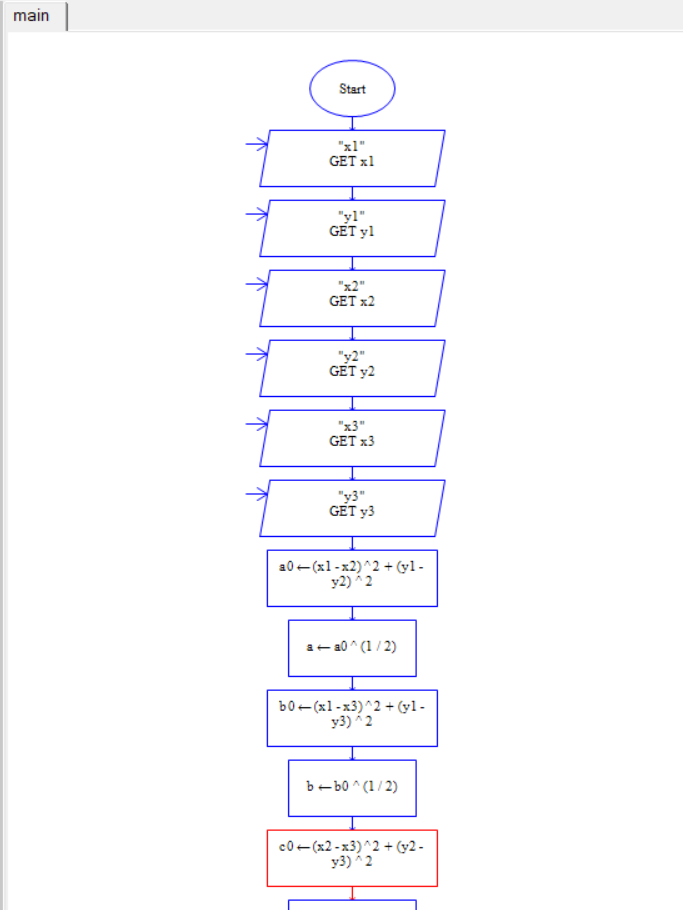
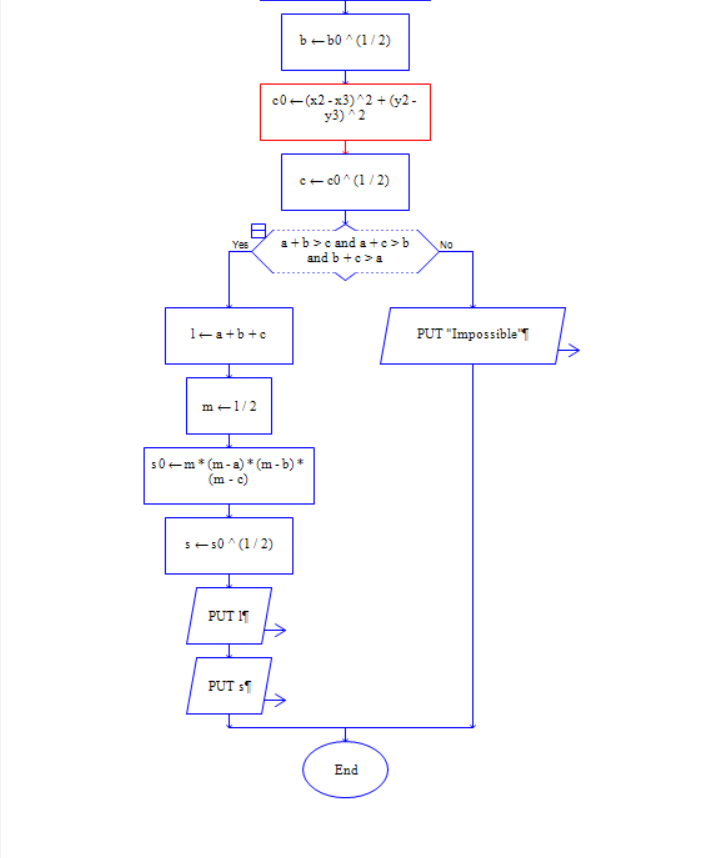
（3）源代码

#include<stdio.h>
#include<math.h>
int main(void)
{
double x1 = 0.0,y1 = 0.0,x2 = 0.0,y2 = 0.0,x3 = 0.0,y3 = 0.0,a = 0.0,b = 0.0,c = 0.0,L = 0.0,A = 0.0,M = 0.0;
scanf("%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3);
a = pow((pow(x1 - x2,2)+pow(y1 - y2,2)),0.5);
b = pow((pow(x1 - x3,2)+pow(y1 - y3,2)),0.5); 
c = pow((pow(x3 - x2,2)+pow(y3 - y2,2)),0.5);
if(a + b > c && a + c > b && b + c > a)
{
	L = a + b + c;
	M = L / 2.0;
	A = pow(M * (M - a) * (M - b) * (M - c),0.5);
	printf("L = %.2f, A = %.2f",L,A);
}
else
{
	printf("Impossible");
}
return 0;
}

（4）实验分析
问题1：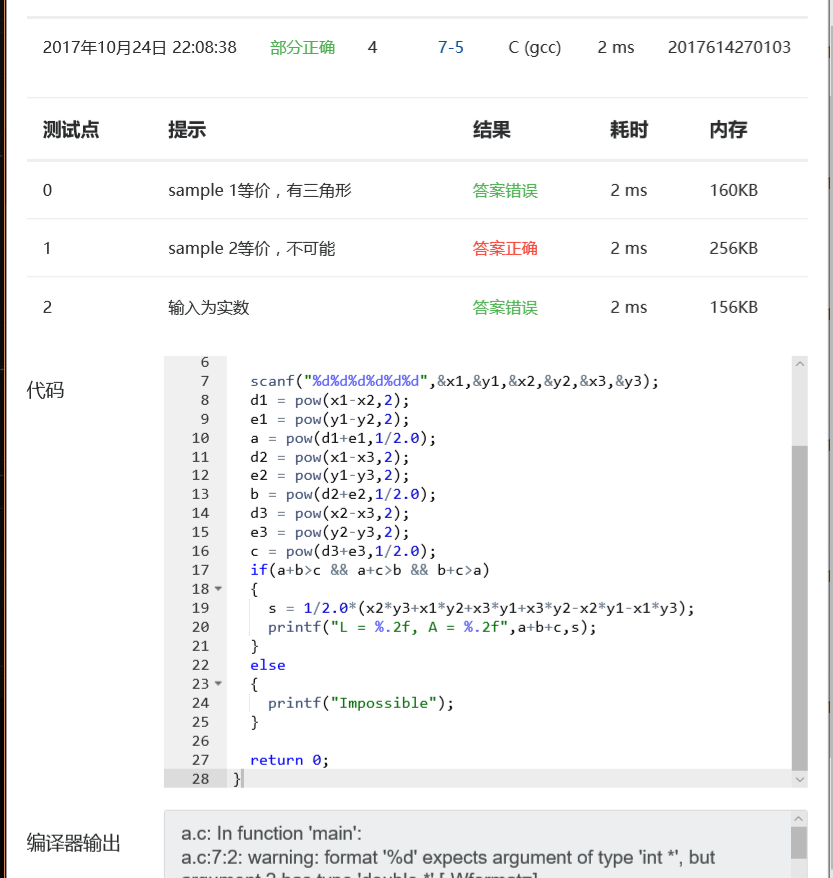
原因：此方法求三角形的面积，有可能会求成面积负数。
解决办法：加入一个判断语句，使得输出的面积均为正数。
问题2：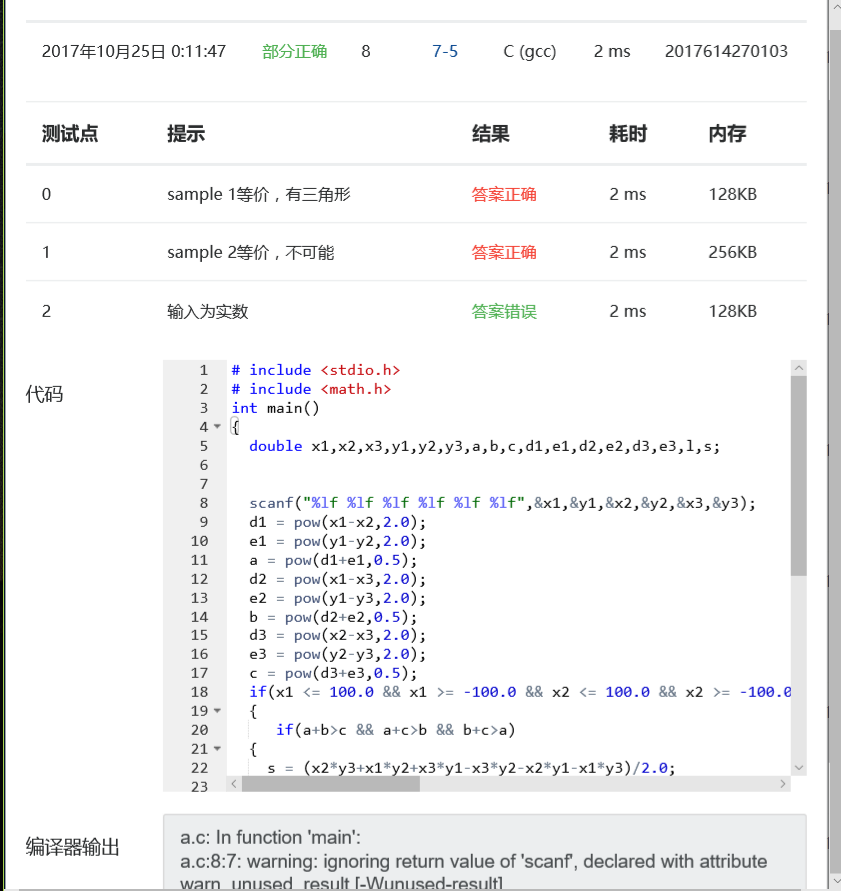
原因：求三角形面积的方法过于繁琐，运算也十分繁琐。
解决办法：将能融合到一起的语句进行融合，把求三角形面积的方法改为更简洁有效的方法。
（5）本题PTA提交列表

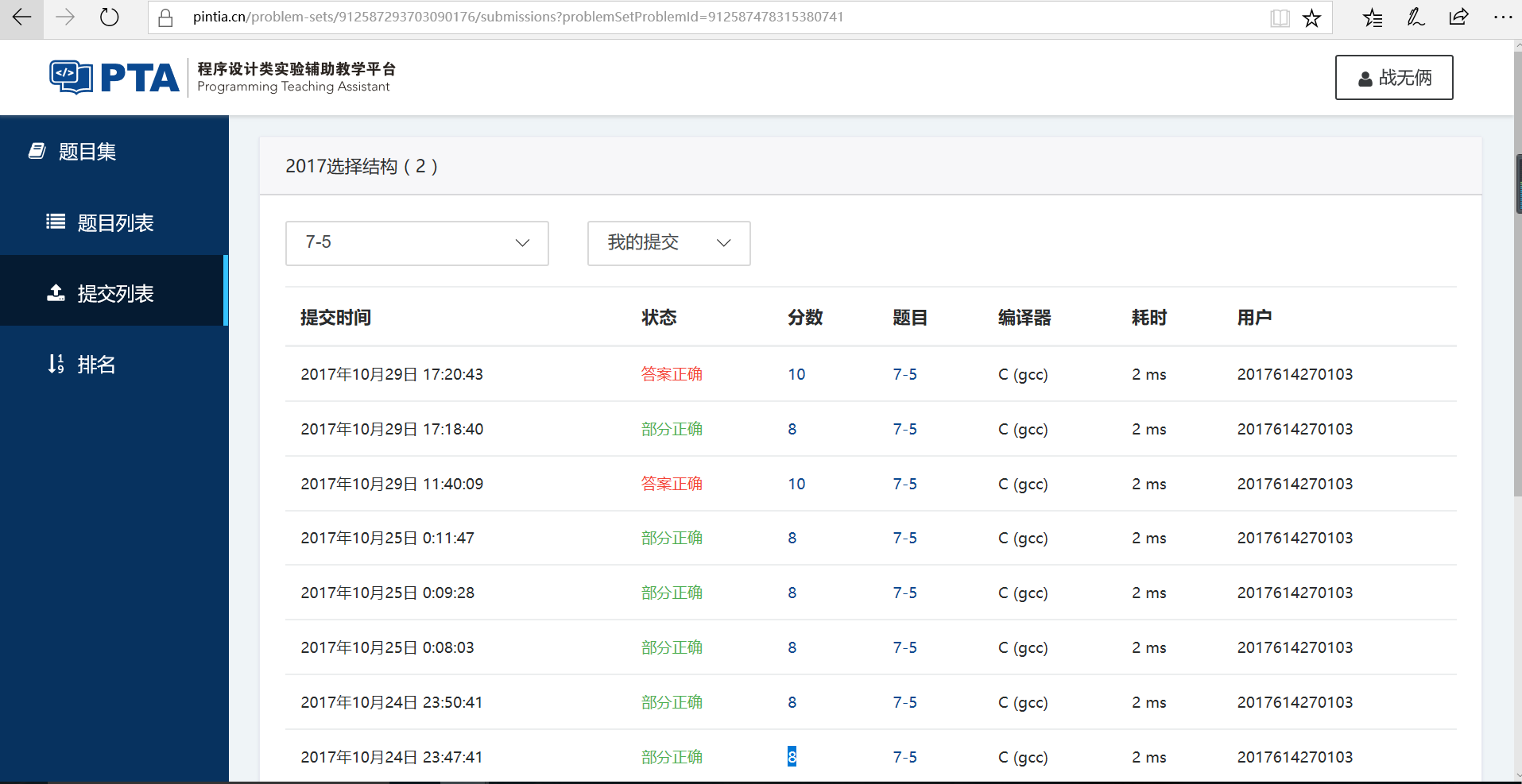
7 两个数的简单计算器
（1）题目
本题要求编写一个简单计算器程序，可根据输入的运算符，对2个整数进行加、减、乘、除或求余运算。题目保证输入和输出均不超过整型范围。
（2）流程图

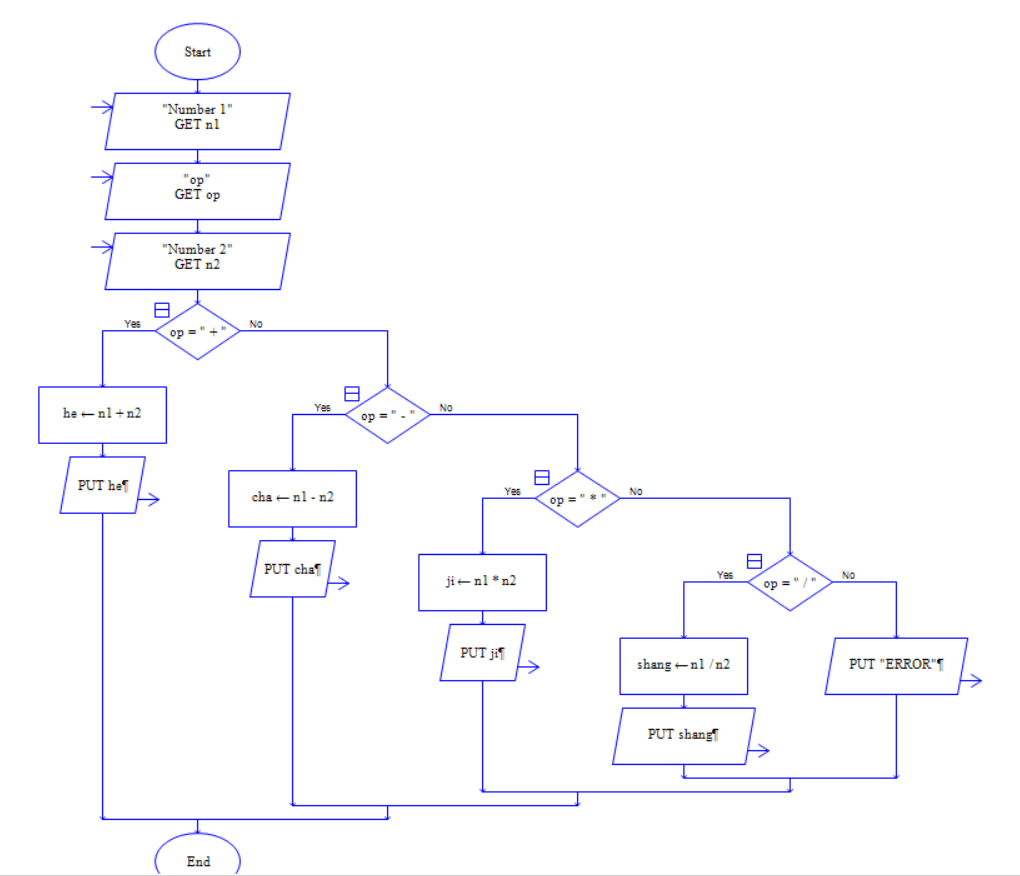
（3）源代码

# include <stdio.h>
# include <stdlib.h>
int main()
{
int a,b,c;
char op;

scanf("%d %c %d",&a,&op,&b);
switch(op)
{
	case '+':c = a+b;printf("%d",c);break;
	case '-':c = a-b;printf("%d",c);break;
	case '*':c = a*b;printf("%d",c);break;
	case '/':c = a/b;printf("%d",c);break;
	case '%':c = a%b;printf("%d",c);break;
	default :printf("ERROR");
}

return 0;			

}

（4）实验分析
无问题
（5）本题PTA提交列表

9 求一元二次方程的根
（1）题目
本题目要求一元二次方程的根，结果保留2位小数。
（2）流程图

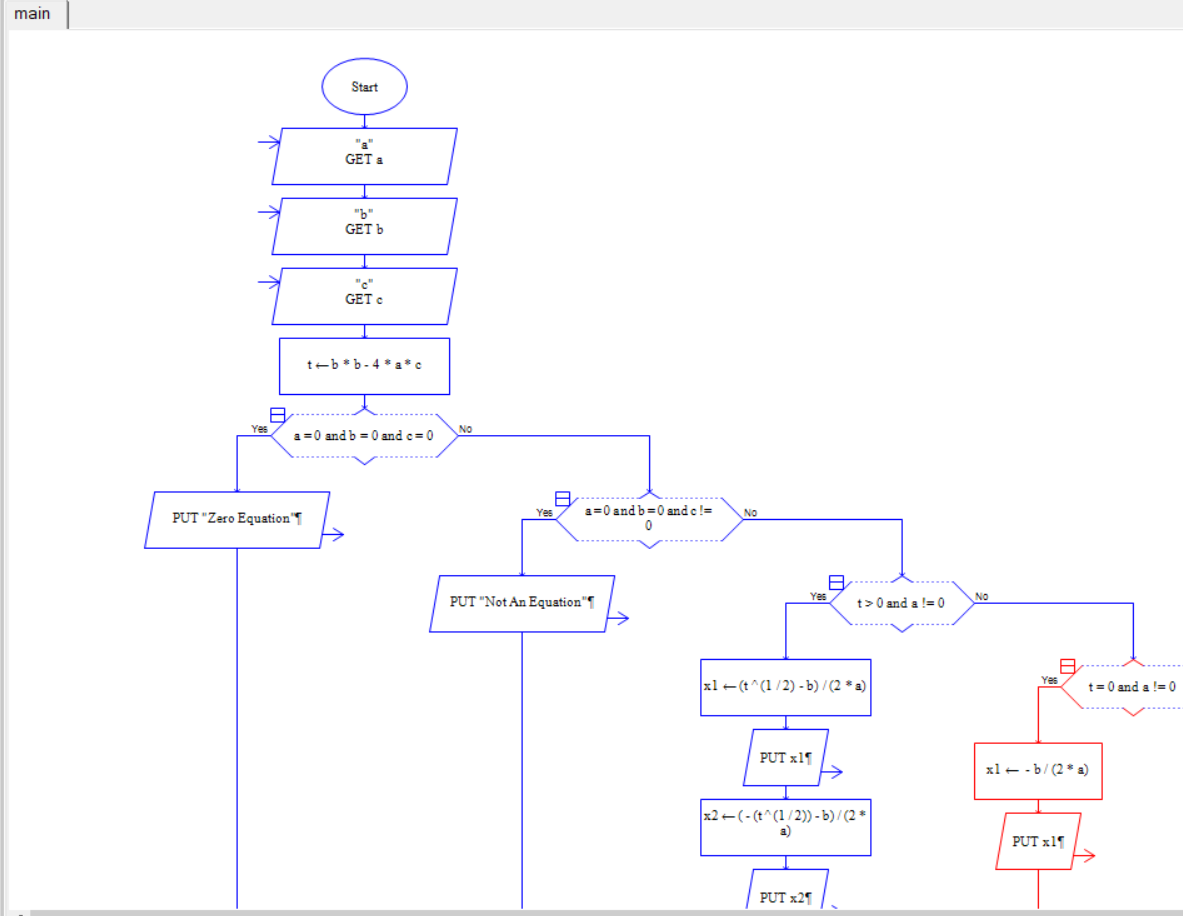
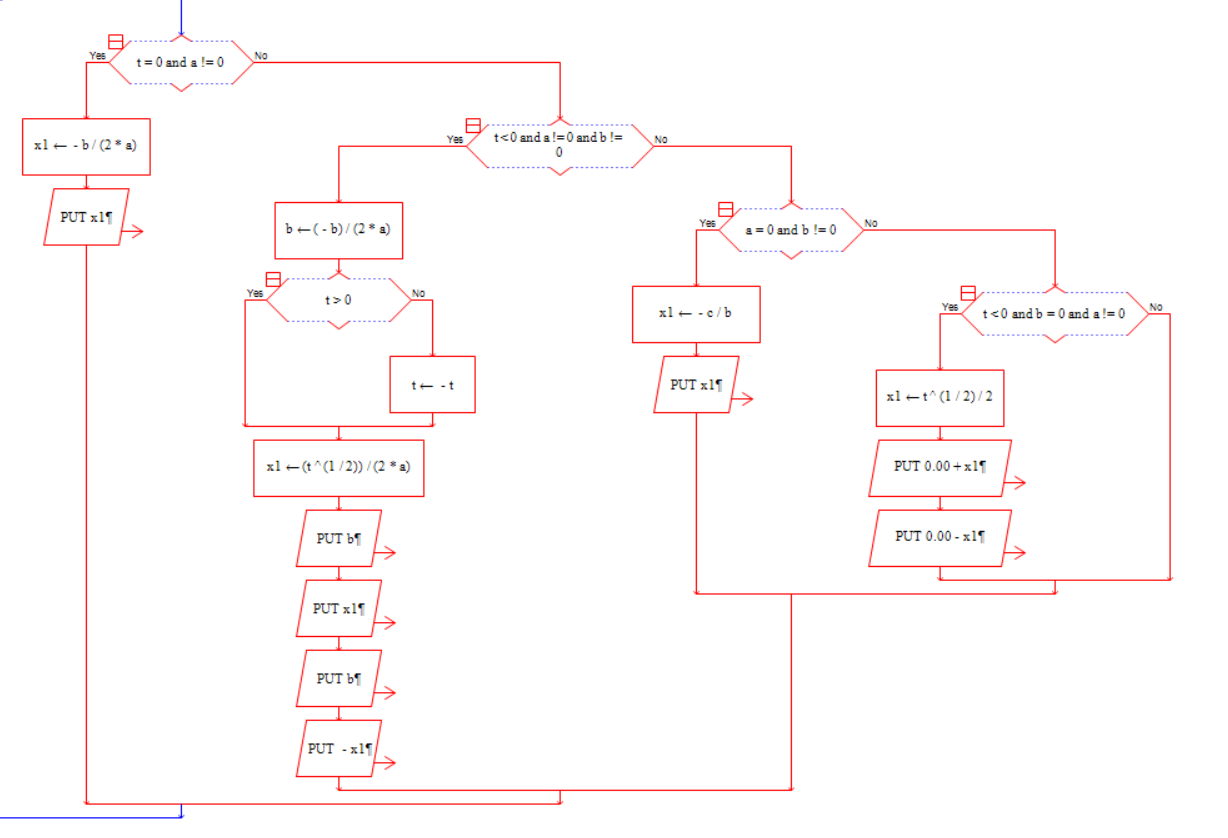
（3）源代码

#include<stdio.h>
#include<math.h>
int main(void)
{
double a = 0.0,b = 0.0,c = 0.0,t = 0.0, x1 = 0.0,x2 = 0.0,m = 0.0;
scanf("%lf%lf%lf",&a,&b,&c);
t = pow(b,2) - 4 * a * c;
if(a == 0 && b == 0 && c == 0)
{
	printf("Zero Equation");
}
if(a == 0 && b == 0 && c != 0)
{
	printf("Not An Equation");
}
if(t > 0 && a != 0)
{
x1 = (sqrt(t) - b) / (2 * a);
x2 = (-b - sqrt(t)) / (2 * a);
printf("%.2f\n%.2f",x1,x2);
}
else if(t == 0 && a !=0)
{
	x1 = -b / (2 * a);
	printf("%.2f",x1);
}
else if(t < 0 && a != 0 && b != 0)
{
	b = -b / ( a * 2);
	t = fabs(t);
	x1 = sqrt(t) / (a * 2);
	printf("%.2f+%.2fi\n",b,x1);
	printf("%.2f-%.2fi",b,x1);
}
else if(a == 0 && b != 0)
{
	x1 = -c / b;
	printf("%.2f",x1);
}
else if(t < 0 && b == 0 && a !=0)
{
	t = fabs(t);
	x1 = sqrt(t) / 2;
	printf("0.00+%.2fi\n",x1);
	printf("0.00-%.2fi",x1);
}

return 0;



}

（4）实验分析
问题1：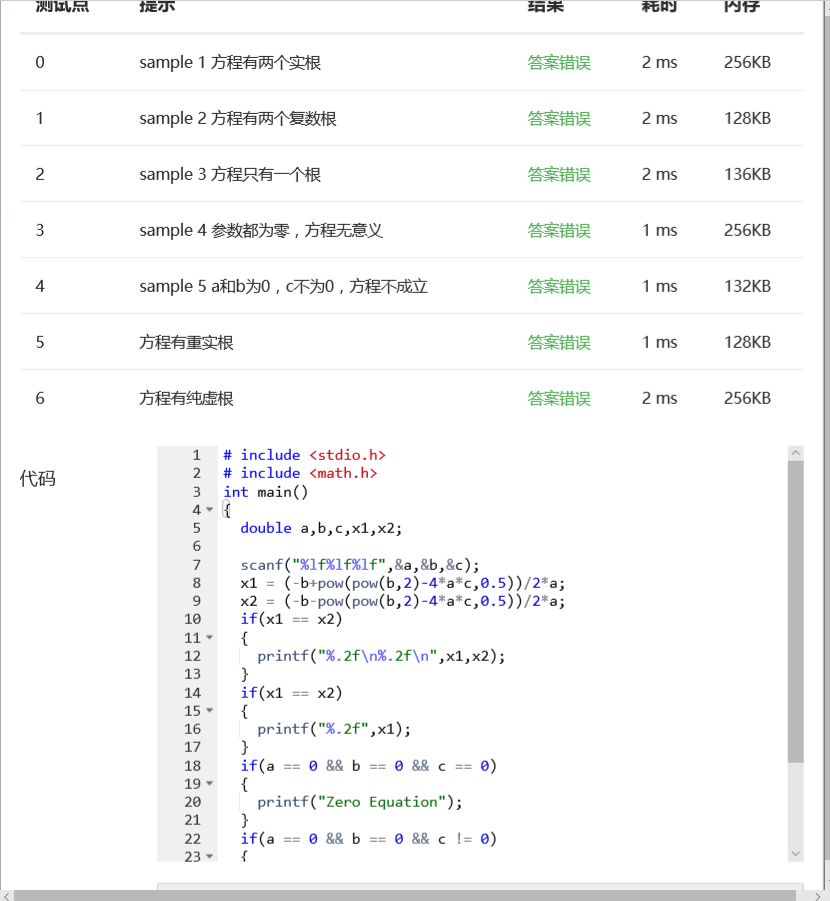
原因：思路不对，求一元二次方程根的方法过于复杂而且不严谨。
解决办法：改变思路，分多次，层层递进的方法，进行求根，以及判断。
问题2：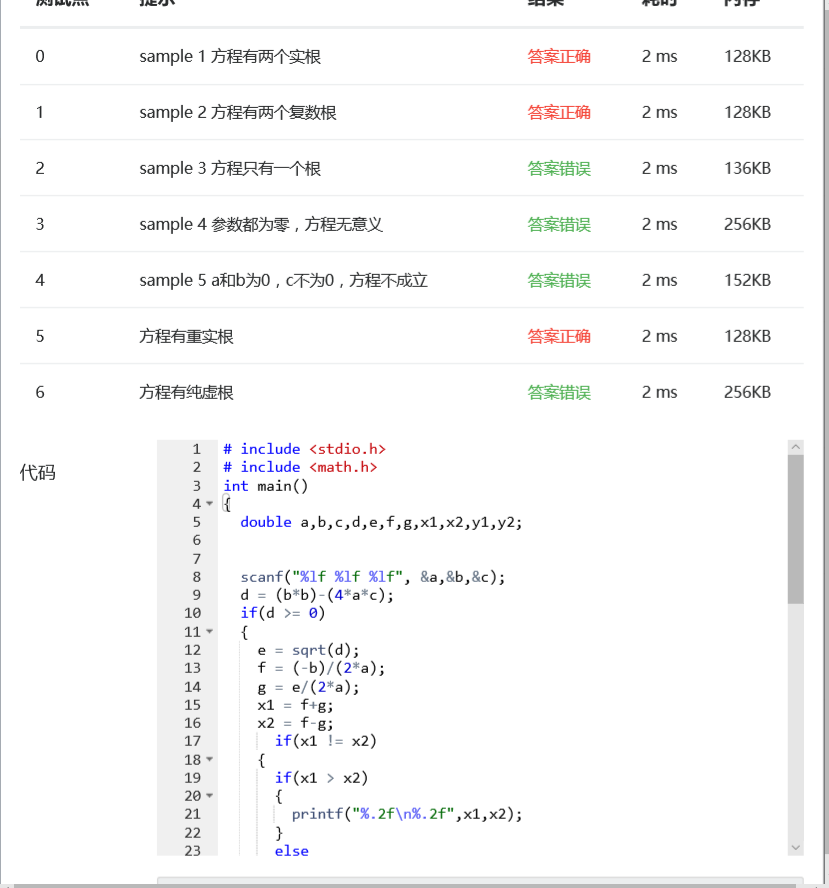
原因：只考虑了一部分情况。
解决办法：把各种情况都考虑到，进行判断。
问题3：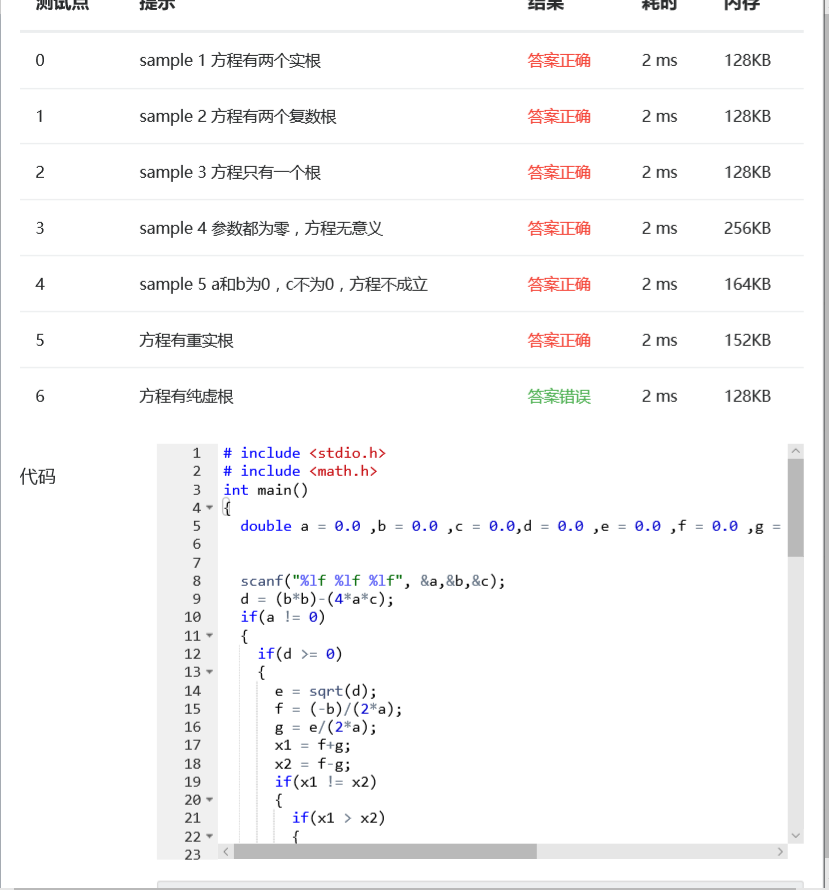
原因：求根的方法依然复杂，纯虚根的输出表达方式不对。
解决办法：把纯虚根的表达方式改为：0.00+%.2fi 以及 0.00-%.2fi。
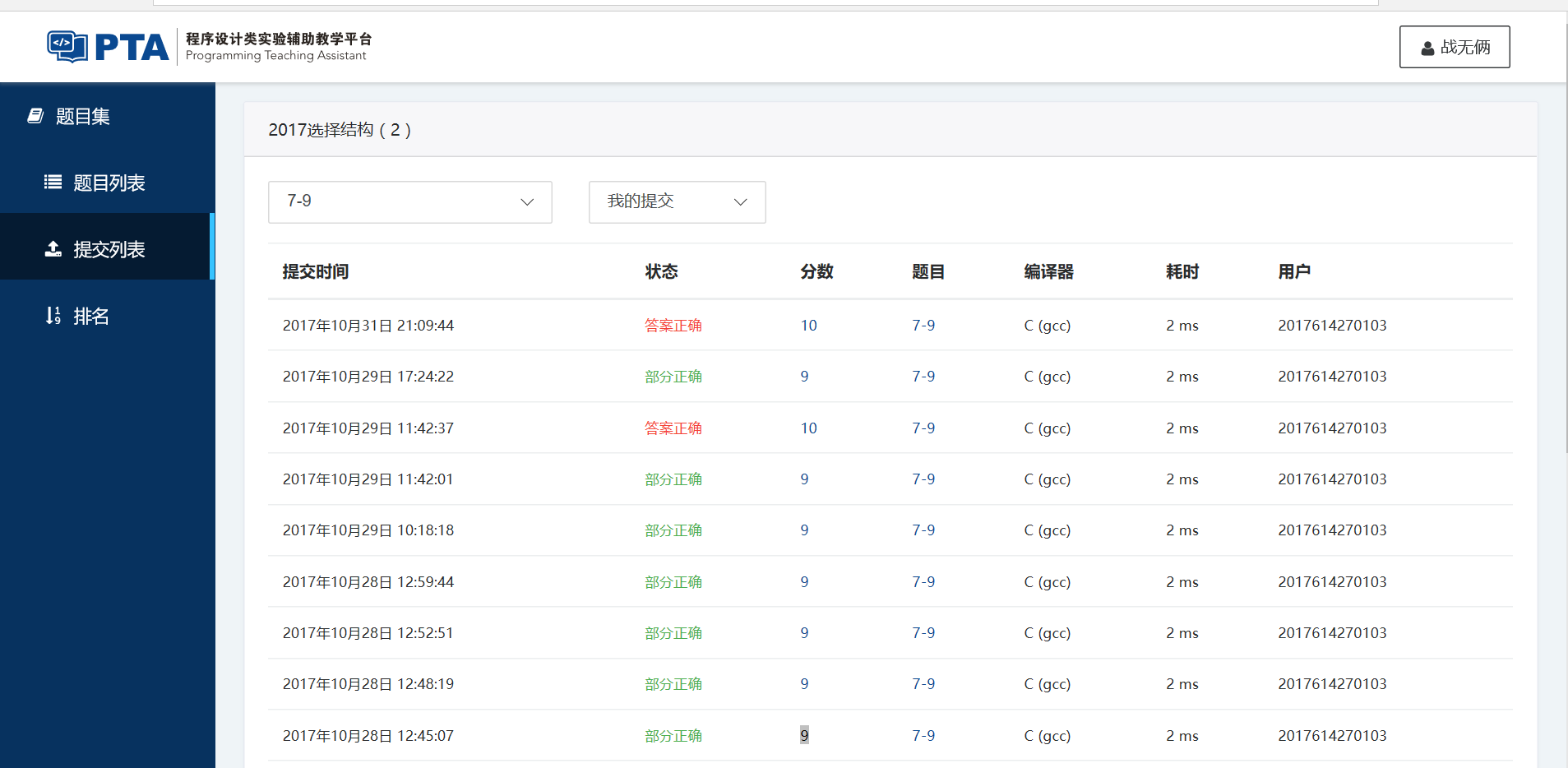
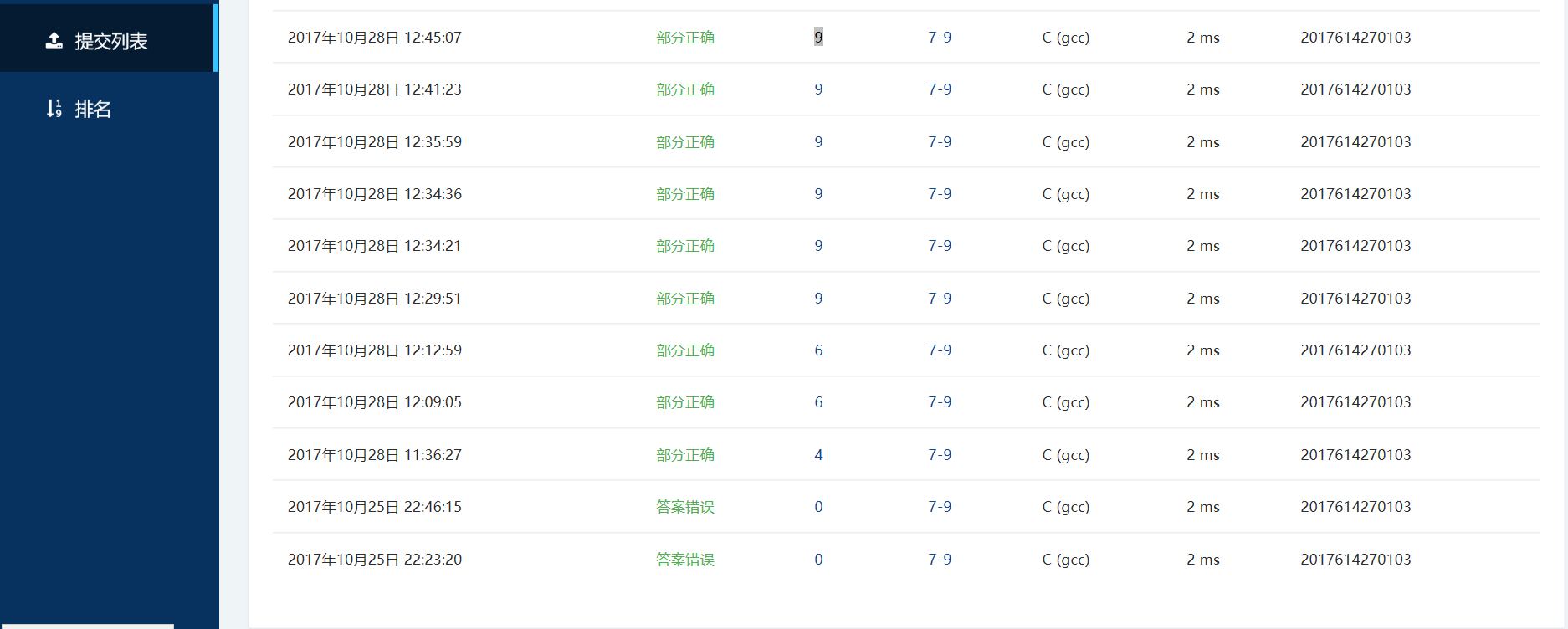
（5）本题PTA提交列表

（四）博客互评
评论一：http://www.cnblogs.com/LLIU/p/7765845.html
评论二：http://www.cnblogs.com/8426224ll/p/7769227.html
评论三：http://www.cnblogs.com/zhaochenyu/p/7769166.html

posted @ 2017-11-03 14:48 曲儿说阅读(388) 评论(1) 编辑收藏举报

刷新页面返回顶部

曲儿说

C语言程序设计第四次作业——选择结构（2）

公告