背包问题

一、01背包

　　　　1.二维形式：

#include<iostream>
#include<algorithm>
using namespace std;
int w[110],v[110],f[110][1100];
int main()
{
    int m,n;
    cin >> m >> n;
    for(int i=1;i<=n;i++){
        cin >> v[i] >> w[i];
    }
    for(int i=1;i<=n;i++){
        for(int j=m;j>=1;j--){
            if(j>=v[i]) f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
            else f[i][j]=f[i-1][j];
        }
    }
    cout << f[n][m];
    return 0;
}

 

 

　　　　当数据较大时，不能使用二维数组，而二维数组可转化为一维数组

for(int j=m;j>=1;j--){
    if(j>=v[i]) f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
    else f[i][j]=f[i-1][j];
}

　　　　将[i]删去，则else部分也可删去

for(int j=m;j>=1;j--){
    if(j>=v[i]) f[i][j]=max(f[j],f[j-v[i]]+w[i]);
} 

　　　　将if与for合并

for(int j=m;j>=v[i];j--){
    f[i][j]=max(f[j],f[j-v[i]]+w[i]);
} 

 

　　　　2.一维形式 ：

//1维 01背包
#include<iostream>
#include<algorithm>
using namespace std;
int w[110],v[110],f[1100];
int main()
{
    int m,n;
    cin >> m >> n;
    for(int i=1;i<=n;i++){
        cin >> v[i] >> w[i];
    }
    for(int i=1;i<=n;i++){
        for(int j=m;j>=v[i];j--){
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout << f[m];
    return 0;
}

 

二、完全背包

　　　　1.二维形式：

#include<iostream>
#include<algorithm>
using namespace std;
int w[110],v[110],f[110][1100];
int main()
{
    int m,n;
    cin >> m >> n;
    for(int i=1;i<=n;i++){
        cin >> v[i] >> w[i];
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(j>=v[i]) f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i]);
            else f[i][j]=f[i-1][j];
        }
    }
    cout << f[n][m];
    return 0;
}

 

　　　　2.一维形式 ：

#include<iostream>
#include<algorithm>
using namespace std;
int w[110],v[110],f[1100];
int main()
{
    int m,n;
    cin >> m >> n;
    for(int i=1;i<=n;i++){
        cin >> v[i] >> w[i];
    }
    for(int i=1;i<=n;i++){
        for(int j=v[i];j<=m;j++){
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout << f[m];
    return 0;
}

 

三、多重背包

　　　　

//1维 多重背包
#include<iostream>
#include<algorithm>
using namespace std;
int w[110],v[110],f[1100],s[110];
int main()
{
    int m,n;
    cin >> m >> n;
    for(int i=1;i<=n;i++){
        cin >> v[i] >> w[i] >> s[i];
    }
    for(int i=1;i<=n;i++){
        for(int k=1;k<=s[i];k++){
            for(int j=m;j>=v[i];j--){
                f[j]=max(f[j],f[j-v[i]]+w[i]);
            }
        }
    }
    cout << f[m];
    return 0;
}

 

 

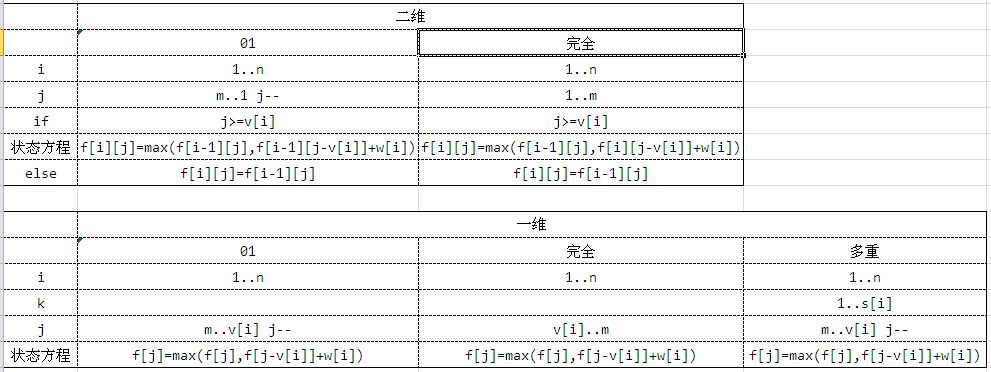
四、背包比较