博客作业06--图
1.学习总结(2分)
1.1图的思维导图
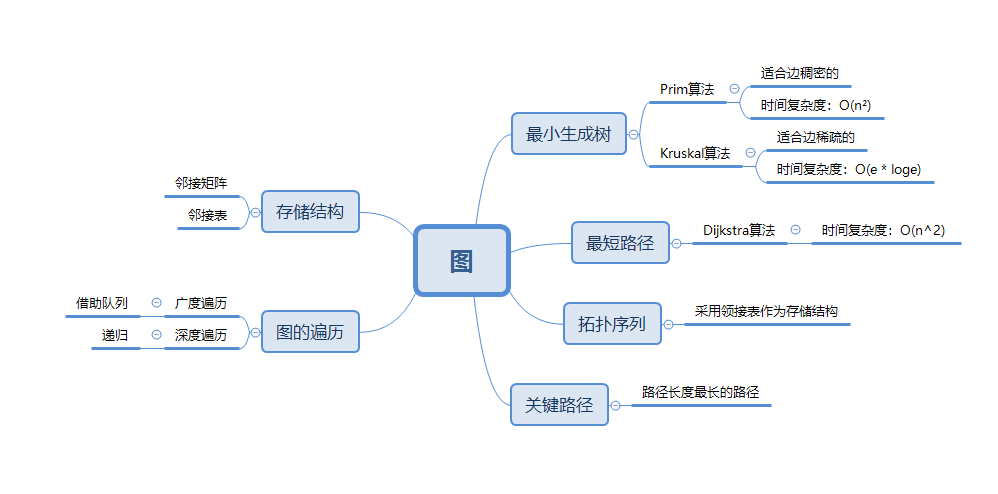
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有:
深度遍历算法:
常用递归的方法。
广度遍历算法:
需要借助队列实现广度遍历。
深度遍历和广度遍历算是比较好理解的,我觉得也是相对于其他几个算法来说比较简单好记的
Prim和Kruscal算法:
用于最小生成树。
两种方法是不同的,prim算法是从某个顶点出发,找跟它距离最近的点,又从新找到的这个点找跟它距离最近的点,一直重复这个过程。kruscal算法是每次都找权值最小的边,并且这些边不会构成一个环,如果会构成环,那就找其他的边。
Dijkstra算法:
用于找最短路径。但是不适合含有负权值的带权图求最短路径。
拓扑排序算法:
任何一个无环有向图,其全部顶点都可以排成一个拓扑序列。拓扑排序的算法emmm对我来说感觉有点点复杂,看了好久才看懂,打代码的时候要看着书才打得出来
Prim、Kruscal、Dijkstra和拓扑排序算法理解是理解了,但是让我自己不看书打代码,我估计是打不出来的
2.PTA实验作业(4分)
2.1 题目1:
7-1 图着色问题
2.2 设计思路(伪代码或流程图)
定义图g
定义整型变量v,e,i,j,n,k,flag,t,count(v顶点数,e边数,k颜色数,n颜色分配方案数)
输入v,e,k的值
调用函数建图
for i=0 to i<n
定义数组color(记录某点的颜色)、apr(用来记录该颜色是否出现过)
两个数组的初始都置为0,flag=0,count=0
for j=0 to j<v
输入该点的颜色
if 该种颜色没出现过
count++,并标记该种颜色已经出现过
if flag=0并且count小于k
for t=0 to t<j
跟j有边的点,如果l两个点的颜色相同
flag=1
end for
end for
if flag=1或者count不等于k
输出No
else
输出Yes
end for
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)


2.4 PTA提交列表说明。

第二次提交,我把if(flag==1||count!=k)中count!=k改成count>k,忘记了小于k的时候也是不行的
2.1 题目2:
7-3 六度空间
2.2 设计思路(伪代码或流程图)
定义整型变量i,j,total,浮点型变量result
输入n、m的值(全局变量)
调用函数建图
for i=1 to i<=n
total=0
for j=1 to j<=n
visited数组初值都置为0(全局变量)
end for
广度遍历第i个人
for j=1 to j<=n
计算visited数组总共有几个人被访问过
end for
计算result的值
输出result
end for
广度遍历
定义整型变量 i,front,rear,count1=0,count2=0.flag=1
定义队列queue[MAXV]
front=rear=-1
标记第v个人已访问
将这个人进入队列
while 队列不为空
v=队头元素
for i=1 to i<=n
if 跟v是朋友并且没有访问过
将这个人进队,并计算出这一层关系一共有几个人
if 这一层关系的所有人都出队列后
层数num加1
if 层数num等于6
结束循环
end while
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)



2.4 PTA提交列表说明。

第一次提交,用的是深度遍历,并且少输出了空格,最大的测试点是答案错误,其他的都是格式错误
第二次提交,加上了空格,测试数据是没有错误的,但是最大的错了 ,后来改用广度遍历,最大的这个测试点就通过了
第三次提交,忘记了添加空格,所以格式错误。。。空格加上去后就对了
2.1 题目3:
7-4 公路村村通
2.2 设计思路(伪代码或流程图)
定义数组lowcost[3001],closest[3001]
定义整型变量min,total=0,count=1,i,j,k,v;
if m<n-1(n代表城市数目,m代表道路数目)即道路不畅通
return -1
for i=0 to i<n
给数组lowcost和closest置初值
end for
for i=1 to i<n
min=INF
for j=0 to j<n
找到最小的边
end for
total=total+最小边的权值
最小边的另一个顶点lowcost[k]置为0
for j=0 to j<n
给数组lowcost和closest重新赋值
end for
end for
if count不等于顶点数
return -1
else
return total的值
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
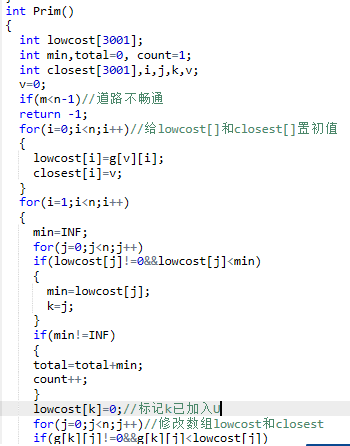

2.4 PTA提交列表说明。

部分正确:当M小于N-1时,不可能有生成树这个测试点运行超时,最大M和N,连通这个测试点答案错误
刚开始没有考虑没有生成树的这种情况,后来直接在Prim函数刚开始就判断M是否小于N-1,如果是就直接return -1,然后两个测试点就都通过了
3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)


3.2 我的总分:
251
得分2.5
4. 阅读代码(必做,1分)
#include <stdio.h>
#include <string.h>
#define N 500
#define INF 501
int g[N][N][2], dis[N + 1], known[N], pay[N];
int main() {
int n, m, s, d, i, j, t1, t2, v;
scanf("%d%d%d%d", &n, &m, &s, &d);
for (i = 0;i < n;i++) {
for (j = 0;j < n;j++) {
g[i][j][0] = INF;
g[i][j][1] = INF;
}
}
while (m--) {
scanf("%d%d%d%d", &i, &j, &t1, &t2);
g[i][j][0] = g[j][i][0] = t1;
g[i][j][1] = g[j][i][1] = t2;
}
memset(known, 0, n*sizeof(int));
for (j = 0;j < n;j++) {
dis[j] = g[s][j][0];
pay[j] = g[s][j][1];
}
dis[s] = 0;
pay[s] = 0;
dis[n] = INF;
while (1) {
v = n;
for (i = 0;i < n;i++) {
if (!known[i] && dis[i] < dis[v])
v = i;
}
if (v == n) break;
known[v] = 1;
for (i = 0;i < n;i++) {
if (!known[i] && g[v][i][0] < INF) {
if (dis[v] + g[v][i][0] < dis[i]) {
dis[i] = dis[v] + g[v][i][0];
pay[i] = pay[v] + g[v][i][1];
}
else if (!known[i] && dis[v] + g[v][i][0] == dis[i] &&
pay[v] + g[v][i][1] < pay[i]) {
pay[i] = pay[v] + g[v][i][1];
}
}
}
}
if(dis[d] < INF)
printf("%d %d", dis[d], pay[d]);
return 0;
}
链接:https://blog.csdn.net/xijujie/article/details/53083511
这是pta上旅游规划的那道题,这个作者用三维数组,将路程的距离跟花费都保存起来,我觉得这个方法蛮不错的。一般我们做到的题都是只求最短路径,所以用到二维数组就可以了,但是这道题还多了花费,用二维就明显不合适。在刚看到这道题的时候,我就在想花费这个要如何处理?后来百度了一下,就看到了这个方法,觉得挺不错的。



