数据结构设计——用队列实现迷宫问题的求解
本篇文章中所有数据结构都是后期整理的,如有问题欢迎指正,转载请注明出处http://www.cnblogs.com/a1982467767/p/8889625.html
1,问题描述
以一个m*n的长方阵表示迷宫,0和1分别表示迷宫中的通路和障碍。迷宫问题要求求出从入口(1,1)到出口(m,n)的一条通路,或得出没有通路的结论。 基本要求: 首先实现一个以链表作存储结构的栈类型,然后编写一个求迷宫问题的非递归程序,求得的通路,其中:(i,j)指示迷宫中的一个坐标, d表示走到下一坐标的方向。 左上角(1,1)为入口,右下角(m,n)为出口。
2.设计思路:
用队列实现迷宫问题的求解;
3.实验代码:
队列实现:
********************************************************************************************
1 //maze_queue.cpp 2 #include<stdio.h> 3 #include<stdlib.h> 4 #include<windows.h> 5 #include"seqqueue.h" 6 7 #define MAX_ROW 12 8 #define MAX_COL 14 9 10 int maze[12][14] = { 11 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 12 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 13 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 1, 14 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 15 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 16 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 17 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 18 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 19 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 20 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 21 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 22 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1 23 }; 24 25 void print_line(void) 26 { 27 int i, j; 28 system("cls"); 29 printf("迷宫如下‘■’代表墙,数字 或者‘☆’表示路径\n"); 30 for (i = 0; i < MAX_ROW; i++){ 31 for (j = 0; j < MAX_COL; j++) 32 if (maze[i][j] == 1) printf("■"); 33 else if (maze[i][j] >= 3){ 34 printf("%2d", maze[i][j] - 2); 35 /*if (i == MAX_ROW-2 && j == MAX_COL-2) printf("★"); 36 else printf("☆");*/ 37 } 38 else printf(" "); 39 printf("\n"); 40 } 41 printf("已找到出路...\n"); 42 printf("可见,用队列求解迷宫问题,可以找出一条最短路径\n"); 43 } 44 45 void visit(int row, int col,PSeqQueue S) 46 { 47 struct point visit_point = { row, col, S->front }; 48 maze[row][col] = 2; 49 In_SeqQueue(S,visit_point); 50 } 51 52 int main() 53 { 54 struct point p = { 1, 1, -1 };//第一个点前驱设为-1,以便后面打印迷宫 55 maze[p.row][p.col] = 2;//遍历过的点设置为2 56 PSeqQueue S = Init_SeqQueue(); 57 In_SeqQueue(S,p); 58 while (!Empty_SeqQueue(S)) 59 { 60 Out_SeqQueue(S,&p); 61 if (p.row == MAX_ROW - 2 && p.col == MAX_COL - 2) 62 break; 63 if (p.col + 1< MAX_COL-1 && maze[p.row][p.col + 1] == 0) 64 visit(p.row, p.col + 1,S); 65 if (p.row + 1< MAX_ROW-1 && maze[p.row + 1][p.col] == 0) 66 visit(p.row + 1, p.col,S); 67 if (p.col - 1 >= 1 && maze[p.row][p.col - 1] == 0) 68 visit(p.row, p.col - 1,S); 69 if (p.row - 1 >= 1 && maze[p.row - 1][p.col] == 0) 70 visit(p.row - 1, p.col,S); //以上是对迷宫的四个方向进行操作 71 } 72 if (p.row == MAX_ROW - 2 && p.col == MAX_COL - 2)//是否为出口 73 { 74 int count = 3; 75 struct point q = { p.row, p.col, p.pre }; 76 while (q.pre != -1)//按照前驱进行查找 77 { 78 q = S->data[q.pre]; 79 count++; 80 } 81 printf("成功找到最短路径,路径倒序输出:\n"); 82 printf("(%d,%d)\n", p.row, p.col); 83 maze[p.row][p.col] = count; 84 while (p.pre!=-1)//按照前驱进行查找 85 { 86 count--; 87 p = S->data[p.pre]; 88 maze[p.row][p.col] = count; 89 printf("(%d,%d)\n", p.row, p.col); 90 } 91 printf("三秒后打印路径......\n"); 92 Sleep(3000); 93 print_line(); 94 } 95 96 else { 97 printf("没有出路\n"); 98 } 99 100 system("pause"); 101 return 0; 102 } 103 //end maze_queue.cpp
************************************************************************************************************
1 //seqqueue.h 2 #include<stdio.h> 3 #include<stdlib.h> 4 #define MAXSIZE 100 5 struct point{ 6 int row, col, pre; 7 }; 8 typedef struct point DataType; 9 typedef struct { 10 DataType data[MAXSIZE]; 11 int front ,rear; 12 }SeqQueue,*PSeqQueue; 13 14 PSeqQueue Init_SeqQueue() 15 { 16 PSeqQueue Q; 17 Q = (PSeqQueue)malloc(sizeof(SeqQueue)); 18 if(Q) 19 { 20 Q->front = 0; 21 Q->rear = 0; 22 } 23 return Q; 24 } 25 26 int Empty_SeqQueue(PSeqQueue Q) 27 { 28 if(Q && Q->front == Q->rear) 29 return 1; 30 else 31 return 0; 32 } 33 34 int In_SeqQueue(PSeqQueue Q,DataType x) 35 { 36 if((Q->rear + 1) % MAXSIZE == Q->front) 37 { 38 printf("队满\n"); 39 return 0; 40 } 41 else 42 { 43 Q->rear = (Q->rear + 1) % MAXSIZE; 44 Q->data[Q->rear] = x; 45 return 1; 46 } 47 } 48 49 int Out_SeqQueue(PSeqQueue Q,DataType *x) 50 { 51 if(Empty_SeqQueue(Q)) 52 { 53 printf("队空"); 54 return 0; 55 } 56 else 57 { 58 Q->front = (Q->front + 1) % MAXSIZE; 59 *x = Q->data[Q->front]; 60 return 1; 61 } 62 } 63 64 int Front_SeqQueue(PSeqQueue Q,DataType *x) 65 { 66 if(Q->front == Q->rear) 67 { 68 printf("队空\n"); 69 return 0; 70 } 71 else 72 { 73 *x = Q->data[(Q->front + 1) % MAXSIZE]; 74 return 1; 75 } 76 } 77 78 void Distroy_SeqQueue(PSeqQueue *Q) 79 { 80 if(*Q) 81 free(*Q); 82 *Q = NULL; 83 }//end seqqueue.h
4.运行结果:
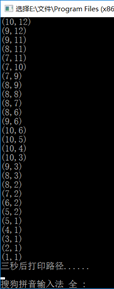
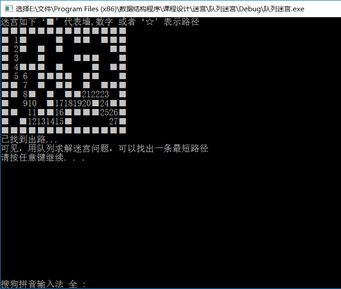
5.实验分析与总结:
在求解迷宫问题中,首先是用栈的来实现操作,一步步入栈出栈,最后找到出路,虽然找到的路劲不是最佳路径,但是这是一种人工智能的算法,符合人的思维方式,是现实生活中人解决迷宫问题的方式;
而用队列实现迷宫问题的求解时,依次探索路径放入队列中,并对每个元素设置好前驱标志,这样一直遍历到终点时,按照前驱进行探索,输出整个迷宫的倒序,并对这些坐标进行编码,再一次遍历迷宫输出路径,即队列实现迷宫的方法;实际操作中,我已开始设置了错误的结构,导致好了一天的时间都没有写完这个迷宫,我开始认为多分叉的树型结构可以很好地解决这个问题,但是在最后探索路劲并返回结果时出现了瓶颈,最后推翻了整个结构,正如老师所说,数据结构的精髓是设计好能更好解决问题的结构,是解决问题的关键所在。




