斜率优化dp
斜率优化
一种常见的优化dp的方法
首先dp要满足求最优状态[最大最小值],而不是方案数
然后根据转移方程列出形如 \(b=y-k\times x\) 的方程
然后根据k的变化和x的变化,用单调队列或者CDQ分治之类的方法维护上下凸函数图像
举一个例子:
\(dp_i= Max(dp_j-val_i*val_j+sum_j-sum_i)\)
那么 \(b=dp_i+sum_i\) ,\(y=dp_j+sum_j\) ,\(x=val_j\) ,\(k=val_i\)
然后根据x,y在坐标系上标点,然后画斜率为k的直线使得之前经过坐标系上的点,易知要维护一个上凸函数
常见套路:
1.x有序,k有序
用单调栈或者单调队列维护函数即可 \(O(n)\)
2.x有序,k无序
用单调栈或者单调队列维护函数,询问时二分 \(O(nlogn)\)
3.x无序
利用CDQ分治,使得x有序 \(O(nlogn)-O(nlog^2n)\)
模板
单调队列[情况1]
struct Slope_queue{
PLL A[M];
int l,r;
Slope_queue(){l=1,r=0;}
void init(){l=1,r=0;}
int sz(){return r-l+1;}
bool empty(){return !sz();}
bool check(PLL A,PLL B,PLL C){
return (B.se-A.se)*(C.fi-B.fi)>=(B.fi-A.fi)*(C.se-B.se);
}
bool check(PLL A,PLL B,LL k){
return (B.se-A.se)<=(B.fi-A.fi)*k;
}
void insert(PLL a){
while(l<r&&check(A[r-1],A[r],a))--r;
A[++r]=a;
}
PLL query(LL k){
while(l<r&&check(A[l],A[l+1],k))++l;
return A[l];
}
}SQ;
单调队列+二分[情况2]
struct Slope_queue{
PLL A[M];
int l,r;
Slope_queue(){l=1,r=0;}
void init(){l=1,r=0;}
bool check(PLL A,PLL B,PLL C){
return (B.se-A.se)*(C.fi-B.fi)>=(B.fi-A.fi)*(C.se-B.se);
}
bool check(PLL A,PLL B,LL k){
return (B.se-A.se)<=(B.fi-A.fi)*k;
}
void Insert(PLL x){
while(l<r&&check(A[r-1],A[r],x))--r;
A[++r]=x;
}
PLL Query(LL k){//根据单调性二分查找
int L=l,R=r-1,res=r;
while(L<=R){
int mid=(L+R)>>1;
if(!check(A[mid],A[mid+1],k)){
res=mid;
R=mid-1;
}
else L=mid+1;
}
return A[res];
}
}SQ;
CDQ分治
void solve(int l,int r){
if(l>=r)return;
int mid=(l+r)>>1;
solve(l,mid);
//sort 或者归并排序 让x有序
//将[l,mid]中满足条件的点都加进单调队列
FOR(i,mid+1,r){
//转移...
}
solve(mid+1,r);//再处理右边的
}
例题 斜率
Description
平面中有 n个点 (xi,yi) ,有 m 条直线,斜率 k 已经确定,需要在给定的 n 个点中,选出一个点 (x,y) ,使得 kx+y最大。
- \(n,m\le 10^5\)
Solution
对于每个条直线,有 $ b=k\times x+y$
将式子化为 $b=y-k\times(-x) $
用单调队列维护上凸包,把点按x从小到大排序后,依次插入队列
然后将询问的k排序[从大到小],根据k弹掉斜率大于当前点的
Code
#include<bits/stdc++.h>
using namespace std;
#define FOR(i,x,y) for(int i=(x),i##_END=(y);i<=i##_END;++i)
#define x first
#define y second
typedef long long LL;
typedef pair<int,int> PII;
const int M=100005;
PII A[M];
int Q[M],Id[M];
LL Ans[M];
bool cmp(int a,int b){
return Q[a]>Q[b];
}
struct Slope_Queue{
PII Q[M];
int l,r;
Slope_Queue(){l=0,r=-1;}
bool chk(PII A,PII B,PII C){
return (LL)(B.y-A.y)*(C.x-B.x)<=(LL)(B.x-A.x)*(C.y-B.y);
}
bool chk(PII A,PII B,int k){
return (LL)(B.y-A.y)>=(LL)(B.x-A.x)*k;
}
void insert(PII a){
while(l<r&&chk(Q[r-1],Q[r],a))--r;
Q[++r]=a;
}
PII query(int k){
while(l<r&&chk(Q[l],Q[l+1],k))++l;
return Q[l];
}
}SQ;
int main(){
int n,m;
scanf("%d%d",&n,&m);
FOR(i,1,n){
scanf("%d%d",&A[i].x,&A[i].y);
A[i].x*=-1;
}
sort(A+1,A+n+1);
FOR(i,1,m){
Id[i]=i;
scanf("%d",&Q[i]);
}
sort(Id+1,Id+n+1,cmp);
FOR(i,1,n)SQ.insert(A[i]);
FOR(i,1,n){
int k=Q[Id[i]];
PII res=SQ.query(k);
Ans[Id[i]]=res.y-(LL)res.x*k;
}
FOR(i,1,m)printf("%lld\n",Ans[i]);
return 0;
}
hihocoder 1529 不上升序列
[斜率优化]
Description
给出一个序列 \(a[1...n]\) ,求构造一个 \(b[1...n]\) ,满足\(b_{i+1}\le b_{i}\),使得 \(\sum\limits _{i=1}^{n} |a_i-b_i|\) 最小 .
- \(n\le 5\times 10^5\)
Solution
关于暴力与转移方程
首先对于暴力转移,定义\(dp_{i,j}\)为转移到i点,权值为j的最小花费.
那么有转移方程 $dp_{i+1,j}= min(dp_{i,k})+|A_i-j| $ [k>=j]
函数图像及证明
然后分析\(dp_{i,j}\) 构成的函数,定义 \(f(x)=dp_i\) ,那么可以得到\(f(x)\)是一个下凸函数 [斜率单调不递减]
首先对于i=1的情况,图像是:
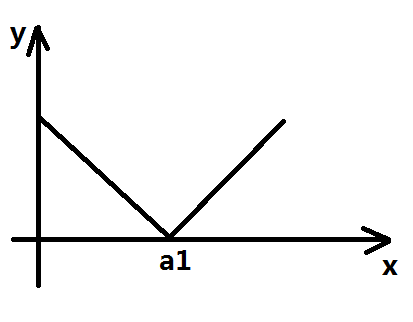
很显然是一个下凸函数
其中y表示花费,x表示b1的取值,a1表示原来第一个点的值
再观察上面给出的转移方程,发现对于一个j,用到的是大于等于自己的k对应的最小值
所以那段下降的函数是无用的
如果要转移到下一层的话,我们就只用管:
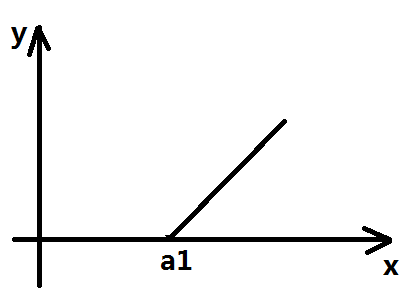
然后加入a2,但考虑a2构成的图像是和上面a1的图像相同的,然后再与修改后的转移图像相叠加,不难发现图像的斜率单调不减
所要维护的东西
由上面的推导可知:
加入一个数之后,图像会有所改变,并且我们不用管斜率小于等于0的部分函数
所以就始终维护一个斜率大于0且单调递增函数即可,并且答案就为那个下凹点
假设我们考虑 \(a_i\) ,那么 \(x< a_i\)的部分的斜率都要 -1,\(x> a_i\)的部分斜率都要 +1
如何维护斜率
加入第一个点后 \(f(x)\) 是一个斜率为1的递增函数
那么就放入\(a_1\),表示 \([a_1,\infty]\) 的局部函数斜率都为1
如果加入一个 \(a_2\)
若\(a_2\ge a_1\) ,那么 \([a_1,a_2]\) 的局部函数斜率变为0 ,\([a_2,\infty]\) 斜率变为2
若\(a_2<a1\) ,那么 \([a_2,a_1]\) 的局部函数斜率变成1,\([a_1,\infty]\) 的斜率变为2
对于第一种情况,可以看做 \([a1,\infty]\) $\to $ \([a1,a2],[a2,a2],[a2,\infty]\) 分别对应 0,1,2三种斜率
对于第二种情况,可以看做 \([a1,\infty]\) $\to $ \([a2,a1],[a1,\infty]\) 分别对应 1,2两种斜率
已知斜率小于等于0的函数部分是不要的
所以对于第一种情况,应该把\(a_1\)这个点给删掉,并加入两个\(a_2\)
而第二种情况,只需加入\(a_2\)即可
发现每次只需要调用最左边的点[即最小值],所以用堆维护即可
如何计算答案
发现对于上述第一种情况,整个函数的下凹点改变了,假设原来凹点为\(f(a_1)=y_1\) ,\(,f(a_2)=y_1+k\times (a_2-a_1),k=1\) ,那么斜率改变后, 凹点位置转移到\(a_2\),对应 \(f(a_2)\)不变,所以答案增大\(a_2-a_1\)
RT

