1.学习总结(2分)
1.1树结构思维导图

1.2 树结构学习体会
- 认识:树,顾名思义就像是树一样,每一根树枝都可能生出0到不等的分支直到最后长出叶子,也就是树结构中分支节点和叶子节点的来由,目前对树的操作都是在二叉树上进行的,所以偶尔也会忘记树除了一对二,也有一对多的关系的。
- 困难:从遍历开始感觉树的许多操作都是建立在递归函数上,所以经常会搞不懂递归出口在哪里,导致程序死循环或者访问错误。一开始的困难也是在不知道如何让树访问到左子树的叶子节点后返回根节点再访问右子树。
- 用处:1.如果把一个人当成一个树的节点,那么且不单单说亲属关系,社会关系也可以用树的形式表达,虽然我还不清楚如何实现,但是依照这种一传多,多载传多的形式,正是当今网络上信息的传递方式; 2.树中有双亲节点和孩子节点和兄弟节点,可以应用于族谱的记录。
(在表达式树这题中,不明白为什么要转换为二叉树,再在二叉树上进行计算,直接计算不是简单明了?)
2.PTA实验作业(4分)
2.1 题目1:6-4 jmu-ds-表达式树
2.2 设计思路
用的是老师上课的思路

最后多了针对字符串读完,但是栈还不为空的情况,思路如下:
初始化化存放运算符栈op.push(‘#’) 存放树节点栈 stacktree
while(栈op 不等于 ‘#’){
定义树指针类型 T1,a,b;分别存放根节点,左孩子树,右孩子树
T1初始化分配内存;
b 等于 栈头; 出栈
a 等于 栈头; 出栈
函数CreateExpTree(T1,a,b,op栈头)
op出栈
T1入栈stacktree
}
函数CreateExpTree是题目给的简单创建树函数
void CreateExpTree(BTree &T,BTree a,BTree b,char ch){ //简单二叉树的创建
T=new BTNode;
T->data=ch;
T->lchild=a;
T->rchild=b;
}
2.3 代码截图
1.创建表达式树
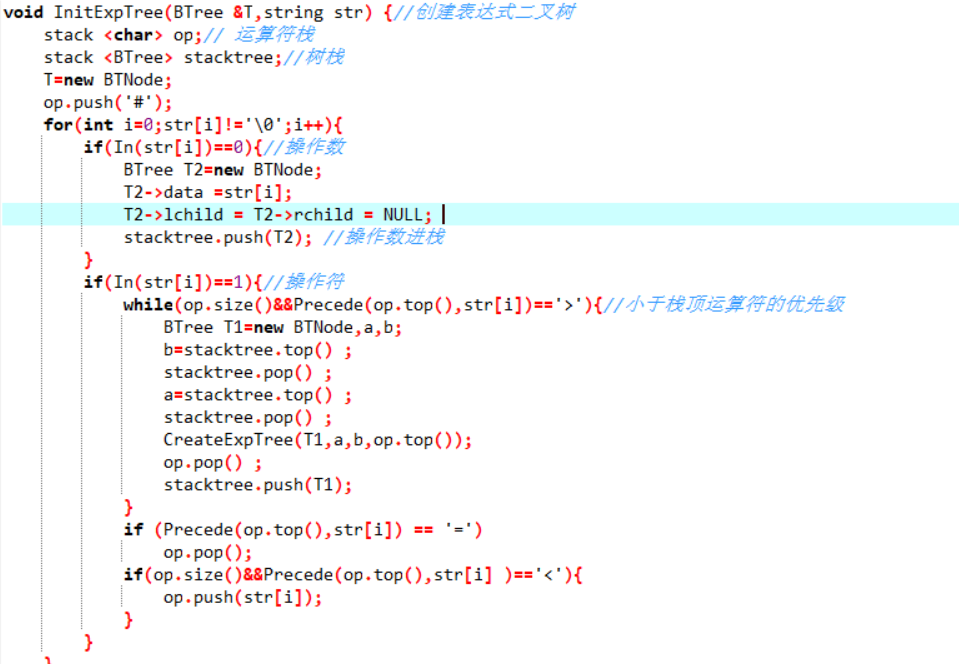

2.计算表达式树
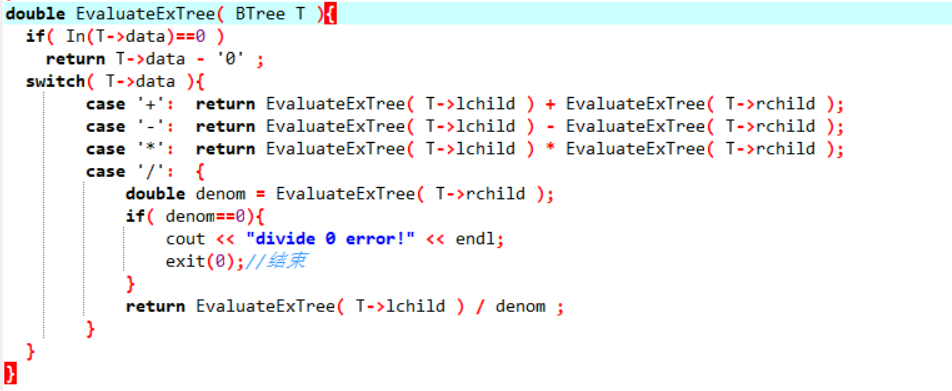
2.4 PTA提交列表说明

虽然提交一次就正确了,但是这题我做了5个小时
最后的错误点在于判断运算符优先等级的顺序,要先判断相等的情况,再判断大于栈顶元素符的情况, 就是要先把左括号弹出,否则就会错误
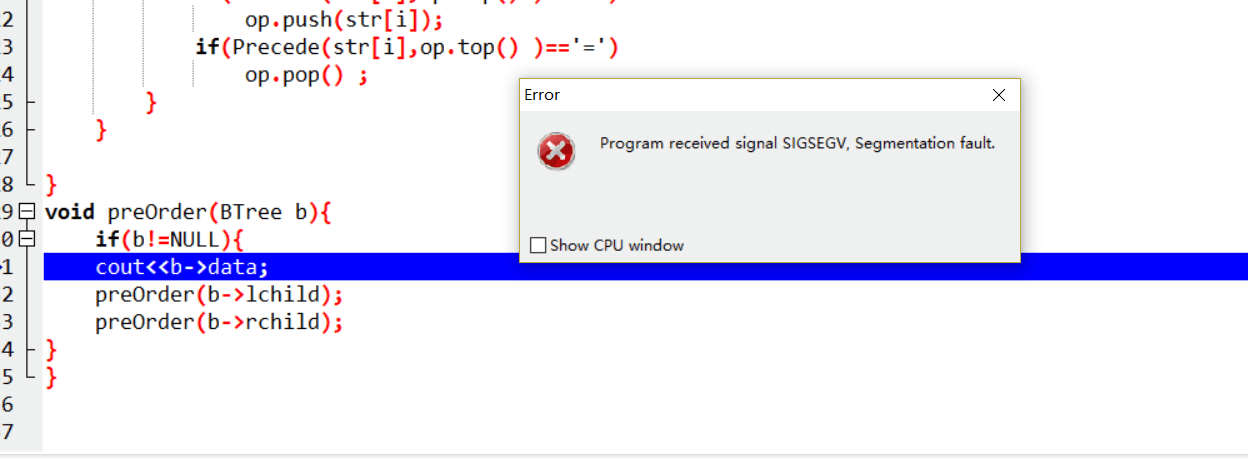
2.1 题目2:7-1 还原二叉树
2.2 设计思路
函数create传参 字符指针类型变量 pre 先序遍历的字符串,in 中序遍历的字符串 , 整型变量 n 包含树的字节数(遍历字符串的长度)
定义树指针类型变量 b 储存根节点
定义整型变量 k储存左子树的长度
定义字符指针类型 p 作循环变量
if 节点数n 小于等于 0
return 树空
初始化b
令b的数据 等于 pre 头数据 即根节点数据
for p=in to p=in+n 遍历 in
if 找到 in中的根节点p
break;
end for
k 等于 左子树长度 p-in
递归
b的左子树 等于 create(pre加一 ,in,左子树长度k)
b的右子树 等于 create(pre加k加一,p加一,右子树长度n 减k加一)
2.3 代码截图
1.还原二叉树(按照课本)

2.高度(课本)

2.4 PTA提交列表说明。

全部都是课本上的代码,一次过。
2.1 题目3:7-8 jmu-ds-二叉树叶子结点带权路径长度和
2.2 设计思路
定义全局整型变量 all =0
传参 树 t,高度 h
if t不为空
if t为叶子节点
all += t节点权值 乘 t节点高度h
end if
end if
递归
传参 节点t的左子树,高度h+1
传参 节点t的右子树,高度h+1
2.3 代码截图

2.4 PTA提交列表说明。

这个是考试的时候做的,所以考试结束后就把代码粘过来了,就一次过。
3.截图本周题目集的PTA最后排名(201721123002)

3.1 PTA排名:23名
3.2 我的得分:2分(180分)
4. 阅读代码(必做,1分)
判断一个树是否为另一个树的子树
#include<iostream>
using namespace std;
struct tnode{
int value;
tnode*left;
tnode*right;
};
//深度优先遍历 在树中寻找节点node 层次遍历更好
tnode * find(tnode* root, tnode* node){
if(root == NULL || node == NULL) return NULL;
if(root->value == node->value) return root;
tnode* tmp=find(root->left,node);
if(tmp) return tmp;
return find(root->right,node);
}
//判断两个树是否相等
bool same(tnode* node1, tnode* node2){
if(node1==NULL && node2==NULL) return 1;
if(node1==NULL && node2!=NULL) return 0;
if(node1!=NULL && node2==NULL) return 0;
if(node1->value == node2->value)
return same(node1->left,node2->left) && same(node1->right,node2->right);
return 0;
}
int isSubTree(tnode* root1, tnode* root2)
{
if(root1==NULL || root2==NULL) return -1;
//首先遍历root1,找到root2对应的节点
tnode* tmp=find(root1,root2);
if(tmp==NULL) return -1;//root2不在root1中
//接下来判断tmp和root2为根的子树是否相等
//cout<<tmp->value<<" "<<root2->value<<endl;
if(same(tmp,root2)) return 1;
else return -1;
}
其实这个代码十分简单,在看到这个题目就可以有思路,但是我的想法是直接在主树上找到子树的根节点后直接再比较孩子节点,
他是在找到根节点后return 该节点,然后再建一个函数进行比较孩子节点,从读的角度上说十分好理解,也是使用了递归函数的方法,代码量少
但其主函数主要用于测试(没有贴出来),没有考虑到存在相同数值根节点的情况以及一棵树中有相同的子树的情况,如果是我做的话应该会有一个以树未全部遍历为条件的循环查找,
5. 代码Git提交记录截图