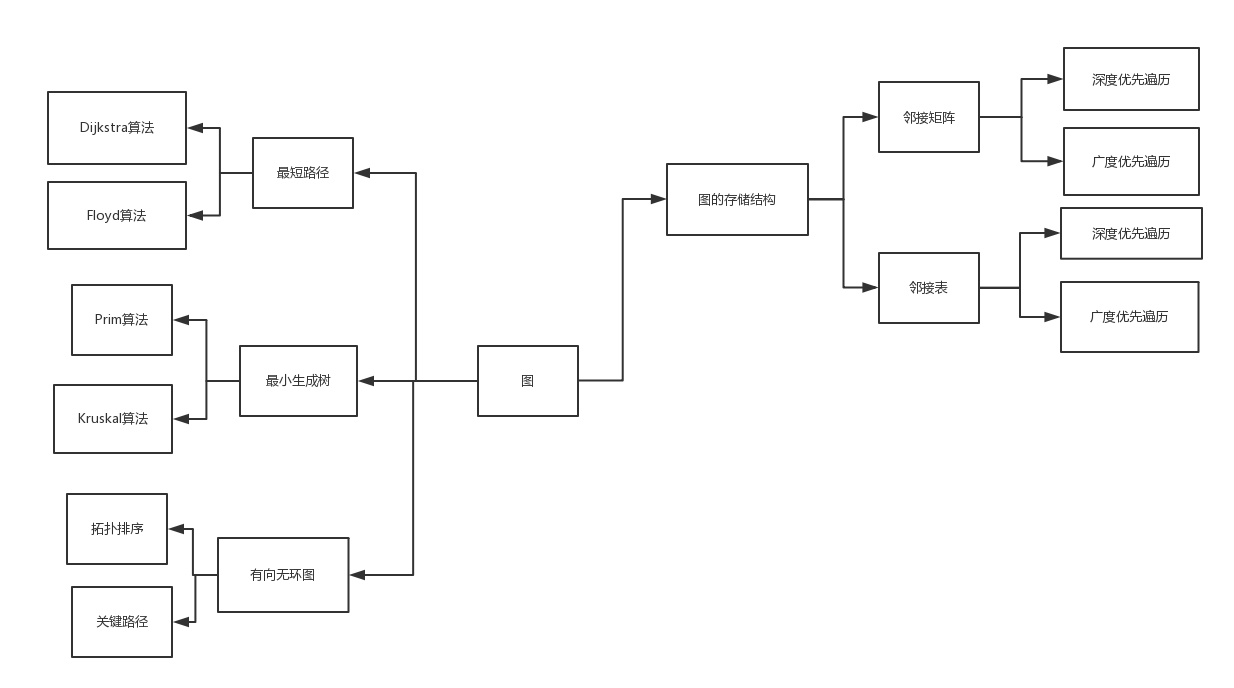
图

1.学习总结

1.1图的思维导图

1.2 图结构学习体会

一、Prim和Kruscal算法是解决最小生成树问题。Prime算法和Kruskal算法，分别从点和边解决了该问题

1. 在一个加权连通图中，顶点集合V，边集合为E

2. 任意选出一个点作为初始顶点,标记为visit,计算所有与之相连接的点的距离，选择距离最短的，标记visit.

3. 重复以下操作，直到所有点都被标记为visit：

在剩下的点钟，计算与已标记visit点距离最小的点，标记visit,证明加入了最小生成树。

二、Dijkstra算法是计算最短路径的算法

1.初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为”起点s到该顶点的距离”[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。

2. 从U中选出”距离最短的顶点k”，并将顶点k加入到S中；同时，从U中移除顶点k。

3. 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。

4. 重复步骤2和3，直到遍历完所有顶点。

三、拓扑排序主要是判断一个有向图是否存在回路，为求有向图的最长路径

2.PTA实验作业

2.1 题目1：排座位

2.2 设计思路

定义x,y,t

调用combine函数

输入x,y

if finds(x)==finds(y)且maps[x][y]!=-1    则输出No problem

否则 if finds(x)==finds(y)且maps[x][y]==-1  则输出 OK but

否则 if finds(x)!=finds(y)且maps[x][y]==-1 则输出No way

否则 输出OK

End 算法

2.3 代码截图

2.4 PTA提交列表说明

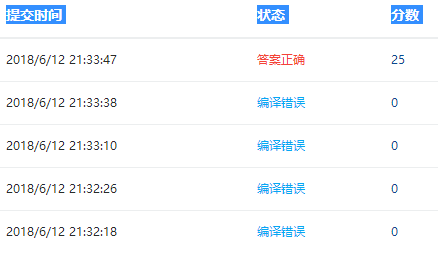
该题运用了c++的语法而编译环境没有转换，刚开始以为是自己哪里有小错误试着修改编译运行才导致多次编译错误

2.1 题目2：公路村村通

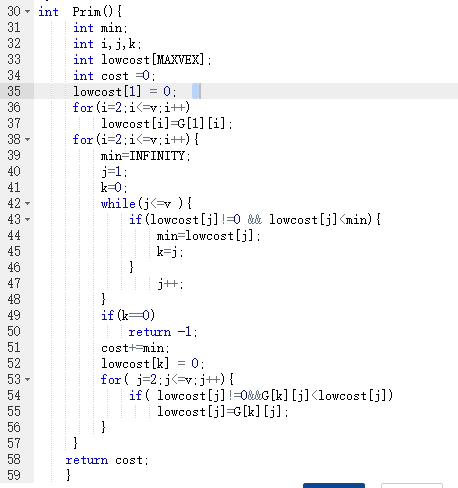
2.2 设计思路

初始化第一个权值为0

if lowcost[j]!=0且lowcost[j]<min  则min=lowcost[j]  k=j 将当前最小值的下标存入k

if k==0 则 不连通

将 lowcost[k]=0 当前顶点置为0

if lowcost[j]!=0且 G[k][j]<lowcost[j[ 则lowcost[j]=G[k][j] 

End 算法

2.3 代码截图

2.4 PTA提交列表说明

编译错误是因为#include忘记在代码的最开始先打，部分正确显示最大N和M连通和最大N和M不连通的段错误 我到现在还找不出原因

2.1 题目3：六度空间

2.2 设计思路

对单个节点的BFS函数

visited[V] = true; count = 1;
level = 0; last = V;
Enqueue(V, Q);
while(!IsEmpty(Q)){ 
  V = Dequeue(Q);
  for ( V 的每个邻接点 W )
	if ( !visited[W] )
        则visited[W] = true;		
        Enqueue(W, Q); count++;tail = W;
对所有节点实现一次
count = BFS(V)
 print(count）

2.3 代码截图

 

2.4 PTA提交列表说明

这个题目老师在上课时有提起，自己试着写了发现虽然知道要用深度优先遍历的方法可是却毫无思路不知道如何下手，最后百度了代码将百度到的正确代码理解了一遍

3.截图本周题目集的PTA最后排名

3.1 PTA排名

 

3.2 我的总分：214分

4. 阅读代码

例题1:QS网络（QS Network）

题意：若两个QS之间要想连网，除了它们间网线的费用外，两者都要买适配器， 求使所有的QS都能连网的最小费用。

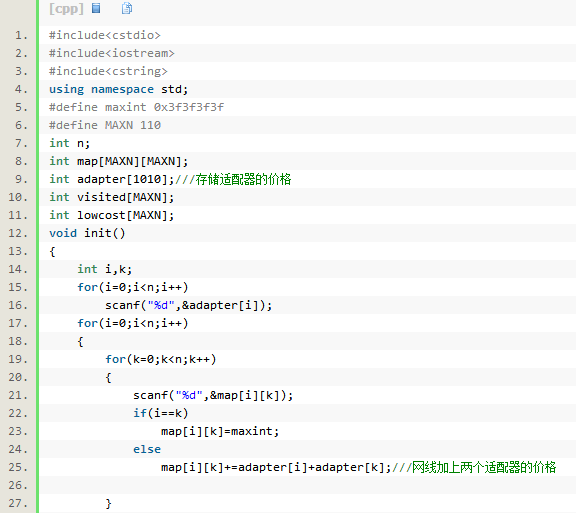
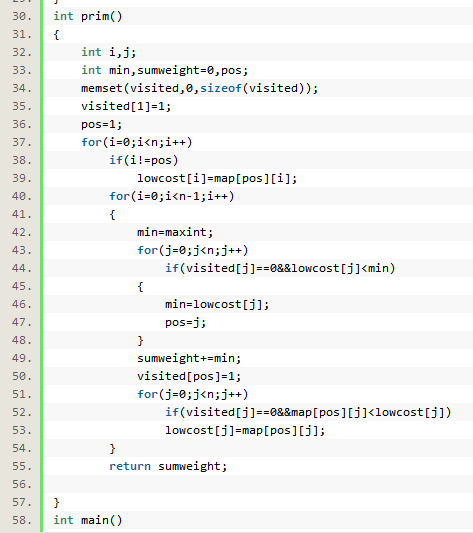
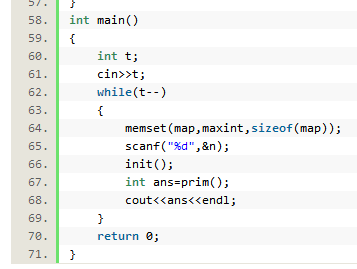
该代码思想在于分析出除了边的权值外，顶点也有权值，因此要想求最小价值，必须算边及顶点的权值和。

 要求最小费用相当于要建立最小生成树，而最小生成树可以利用Prim算法，然后再计算总的权值