我终于明白了的马拉车算法———感谢我们学校的大佬

A:马拉车是什么？

Q:是一种求回文子串（你也可以用它来去最长回文子串）的方法（速度很快）

A:有什么意义？

Q:证明了学好写暴力，走遍天下都不怕的道理

马拉车算法的精髓就是把之前匹配过的字符串结果放到后面来使用

小技巧

一个回文串它的对称中心可能是某个字符（aba），也可能是某两个字符之间（aa），理论上我们应该分类讨论对吧？但实际上我们很懒，所以我们把字符串变成这样（#a#a#）(#a#b#a#)

这样一来，无论是什么字符串，它的长度都是奇数，只需要一种枚举方式就可以了（奇数的枚举方式，但同时可以枚举的偶数的情况）

中心操作：枚举对称轴，有对称轴向左右两边枚举

r[i]表示以i为中点，向左右扩展回文串，所能到达的最大半径是多少

由于我们是从右往左枚举马拉车，所以从0~pos的所有数的最长半径都已经做出来了，是可用的

0~max_r就是我们已知的最大范围

在这个基础上，我们在pos~max_r的范围枚举i,并做j是关于pos的对称轴，r[j]是已知的

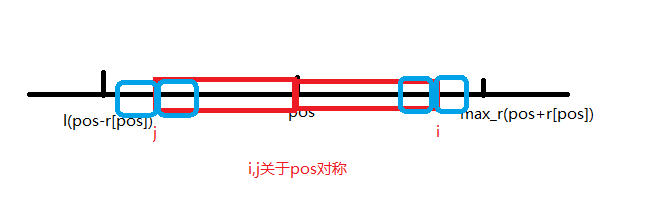
接下来我们开始求关于r[i]，当i+r[i]<max这个时候我们就可以用之前求过的r[j]来覆盖i这个位置，减少了冗余计算（回文串的对称性）

但不排除会存在i+r[i]>max_r 的情况，这个时候就不在我们的控制范围之内了，那我们怎么办？暴力枚举。

在把pos转到i的位置继续执行上述操作

具体代码如下

void Manacher(){
    for (int i=0;t[i];++i,len+=2){
        s[i<<1]='#';
        if (t[i]>='A'&&t[i]<='Z') s[i<<1|1]=t[i]-'A'+'a';
        else s[i<<1|1]=t[i];
    }
    s[len++]='#';
    int max_r=0,pos=0;
    for (int i=0;i<len;++i){
        if (max_r>i) r[i]=min(max_r-i,r[2*pos-i]);
        else r[i]=0;
        while (i+r[i]+1<len&&i-r[i]-1>=0&&s[i+r[i]+1]==s[i-r[i]-1]) r[i]++;
        if (r[i]+i>max_r){
            max_r=r[i]+i;
            pos=i;
        }
    }
}
//马拉车

最后扫一遍r[i]求出max_r[i]，max_r[i]-1就是我们要的最长回文子串的长度