[HAOI2018]苹果树

题目描述

小 C 在自己家的花园里种了一棵苹果树, 树上每个结点都有恰好两个分支. 经过细心的观察, 小 C 发现每一天这棵树都会生长出一个新的结点.

第一天的时候, 果树会长出一个根结点, 以后每一天, 果树会随机选择一个当前树中没有长出过结点 的分支, 然后在这个分支上长出一个新结点, 新结点与分支所属的结点之间连接上一条边.

小 C 定义一棵果树的不便度为树上两两结点之间的距离之和, 两个结点之间 的距离定义为从一个点走到另一个点的路径经过的边数.

现在他非常好奇, 如果 NNN 天之后小 G 来他家摘苹果, 这个不便度的期望 EEE 是多少. 但是小 C 讨厌分数, 所以他只想知道 E×N!E \times N !E×N! 对 PPP 取模的结果, 可以证明这是一个整数.

输入输出格式

输入格式：

从标准输入中读入数据. 一行两个整数 NNN (N<=2000), PPP .

输出格式：

输出到标准输出中. 输出一个整数表示答案．

输入输出样例

输入样例#1： 复制 
3 610745795
输出样例#1： 复制 
24
输入样例#2： 复制 
305 1000000007
输出样例#2： 复制 
865018107

说明

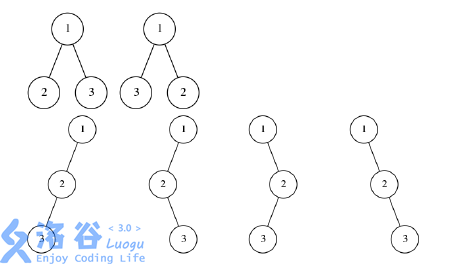
Explanation

以上是所有 N=3N = 3N=3 时可能的苹果树形态, 其中编号表示这个结点是第几天生 长出来的, 显然每种情况两两结点的距离均为 444 .

传送门

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<cmath>
 6 using namespace std;
 7 int fac[2001],C[2001][2001],F[2001][2001],n,Mod,ans;
 8 int main()
 9 {int i,j;
10   cin>>n>>Mod;
11   fac[0]=1;
12   for (i=1;i<=n;i++)
13     fac[i]=1ll*fac[i-1]*i%Mod;
14   for (i=0;i<=n;i++)
15     {
16       C[i][0]=1;
17       for (j=1;j<=i;j++)
18     C[i][j]=(C[i-1][j-1]+C[i-1][j])%Mod;
19     }
20   for (i=1;i<=n;i++)
21     {
22       F[i][0]=1;
23       for (j=1;j<=n;j++)
24     F[i][j]=1ll*F[i][j-1]*(i+j-2)%Mod;
25     }
26   for (i=2;i<=n;i++)
27     {
28       for (j=n-i+1;j>=1;j--)
29     {
30       ans=(ans+(1ll*j*(n-j)%Mod*C[n-i][j-1]%Mod*fac[j]%Mod*F[i][n-j-i+1]%Mod*fac[i]%Mod))%Mod;
31     }
32     }
33   cout<<ans;
34 }

 

posted @ 2018-04-28 22:02  Z-Y-Y-S  阅读(498)  评论(0)  编辑  收藏  举报