[CTSC2017]吉夫特

题目描述

简单的题目，既是礼物，也是毒药。

B 君设计了一道简单的题目，准备作为 gift 送给大家。

输入一个长度为 n 的数列 a1, a2, ... , an 问有多少个长度大于等于 2 的不上升的子序列

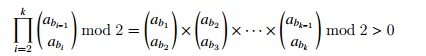
输出这个个数对 1000000007 取模的结果。

G 君看到题目后，为大家解释了一些基本概念。

我们选择任意多个整数 bi 满足

1 ≤ b1 < b2 < · · · < b_{k−1} < bk ≤ n

我们称 a_b1, a_b2, ... , a_bk 是 a 的一个子序列。

如果这个子序列同时还满足

ab1 ≥ ab2 ≥ · · · ≥ abk−1 ≥ abk

我们称这个子序列是不上升的。

组合数 (m n ) 是从 n 个互不相同的元素中取 m 个元素的方案数。

这里要特别注意，因为我们只考虑不上升子序列，所以在求组合数的过程中，一定满足 n ≥ m。

我们在这里强调取模 x mod y 的定义：

x mod y = x − ⌊x/y⌋ × y

其中 ⌊n⌋ 表示小于等于 n 的最大整数。

x mod 2 > 0，就是在说 x 是奇数。

与此同时，经验告诉我们一个长度为 n 的序列，子序列个数有 O(2n) 个，所以我们通过对答案取模来避免输出过大。

B 君觉得 G 君说的十分有道理，于是再次强调了这些基本概念。

最后， G 君听说这个题是作为 gift 送给大家，她有一句忠告。

“Vorsicht, Gift!”

“小心. . . . . .剧毒！ ”

输入输出格式

输入格式：

 

第一行一个整数 n。

接下来 n 行，每行一个整数，这 n 行中的第 i 行，表示 ai。

 

输出格式：

 

一行一个整数表示答案。

 

输入输出样例

输入样例#1： 复制

4
15
7
3
1

输出样例#1： 复制

11

说明

• 对于前 10% 的测试点， n ≤ 9, 1 ≤ ai ≤ 13；

• 对于前 20% 的测试点， n ≤ 17, 1 ≤ ai ≤ 20；

• 对于前 40% 的测试点， n ≤ 1911, 1 ≤ ai ≤ 4000；

• 对于前 70% 的测试点， n ≤ 2017；

• 对于前 85% 的测试点， n ≤ 100084；

• 对于 100% 的测试点， 1 ≤ n ≤ 211985, 1 ≤ ai ≤ 233333。所有的 ai 互不相同，也就是说不存在 i, j 同时满足 1 ≤ i < j ≤ n 和 ai = aj。

 众所周知,$C_{n}^{m}$

是奇数时，有$(n&m)==m$

设f[i]为i这个数为结尾的个数

枚举i的子集，然后判断位置是否在它后面，然后往后转移

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long lol;
lol f[2500001],ans,Mod=1e9+7;
int id[2500001],a[2500001],N,n;
int main()
{int i,j;
  cin>>n;
  for (i=1;i<=n;i++)
    {
      scanf("%d",&a[i]);
      id[a[i]]=i;
      f[a[i]]=1;
      N=max(N,a[i]);
    }
  for (i=1;i<=n;i++)
      {
    for (j=(a[i]-1)&a[i];j;j=((j-1)&a[i]))
      if (id[j]>i)
        {
          f[j]=(f[j]+f[a[i]]);
          if (f[j]>=Mod) f[j]-=Mod;
        }
      }
  for (i=1;i<=n;i++)
    ans+=(f[a[i]]-1),ans%=Mod;
  cout<<ans;
}