codeforces 920E Connected Components?
You are given an undirected graph consisting of n vertices and 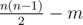 edges. Instead of giving you the edges that exist in the graph, we give you m unordered pairs (x, y) such that there is no edge between x and y, and if some pair of vertices is not listed in the input, then there is an edge between these vertices.
edges. Instead of giving you the edges that exist in the graph, we give you m unordered pairs (x, y) such that there is no edge between x and y, and if some pair of vertices is not listed in the input, then there is an edge between these vertices.
You have to find the number of connected components in the graph and the size of each component. A connected component is a set of vertices X such that for every two vertices from this set there exists at least one path in the graph connecting these vertices, but adding any other vertex to X violates this rule.
The first line contains two integers n and m (1 ≤ n ≤ 200000, 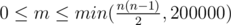 ).
).
Then m lines follow, each containing a pair of integers x and y (1 ≤ x, y ≤ n, x ≠ y) denoting that there is no edge between x and y. Each pair is listed at most once; (x, y) and (y, x) are considered the same (so they are never listed in the same test). If some pair of vertices is not listed in the input, then there exists an edge between those vertices.
Firstly print k — the number of connected components in this graph.
Then print k integers — the sizes of components. You should output these integers in non-descending order.
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #include<vector> 7 #include<queue> 8 using namespace std; 9 int n,m,nxt[200001],lst[200001],ans[200001],cnt; 10 bool vis[200001],pd[200001]; 11 queue<int>Q; 12 vector<int>G[200001]; 13 void delet(int x) 14 { 15 nxt[lst[x]]=nxt[x]; 16 lst[nxt[x]]=lst[x]; 17 } 18 int main() 19 {int i,u,v,j; 20 cin>>n>>m; 21 for (i=1;i<=m;i++) 22 { 23 scanf("%d%d",&u,&v); 24 G[u].push_back(v); 25 G[v].push_back(u); 26 } 27 for (i=1;i<n;i++) nxt[i]=i+1,lst[i+1]=i; 28 nxt[0]=1; 29 for (i=1;i<=n;i++) 30 if (vis[i]==0) 31 { 32 ans[++cnt]=1;vis[i]=1; 33 Q.push(i);delet(i); 34 while (Q.empty()==0) 35 { 36 int u=Q.front(); 37 Q.pop(); 38 for (j=0;j<G[u].size();j++) 39 if (vis[G[u][j]]==0) pd[G[u][j]]=1; 40 for (j=nxt[0];j;j=nxt[j]) 41 { 42 if (pd[j]==0) 43 { 44 vis[j]=1; 45 ans[cnt]++; 46 Q.push(j); 47 delet(j); 48 } 49 else pd[j]=0; 50 } 51 } 52 } 53 sort(ans+1,ans+cnt+1); 54 cout<<cnt<<endl; 55 for (i=1;i<cnt;i++) 56 printf("%d ",ans[i]); 57 cout<<ans[cnt]<<endl; 58 }


