codeforces 809E Surprise me!

Tired of boring dates, Leha and Noora decided to play a game.

Leha found a tree with n vertices numbered from 1 to n. We remind you that tree is an undirected graph without cycles. Each vertex v of a tree has a number a_v written on it. Quite by accident it turned out that all values written on vertices are distinct and are natural numbers between 1 and n.

The game goes in the following way. Noora chooses some vertex u of a tree uniformly at random and passes a move to Leha. Leha, in his turn, chooses (also uniformly at random) some vertex v from remaining vertices of a tree (v ≠ u). As you could guess there are n(n - 1) variants of choosing vertices by players. After that players calculate the value of a function f(u, v) = φ(a_u·a_v) · d(u, v) of the chosen vertices where φ(x) is Euler's totient function and d(x, y) is the shortest distance between vertices x and y in a tree.

Soon the game became boring for Noora, so Leha decided to defuse the situation and calculate expected value of function f over all variants of choosing vertices u and v, hoping of at least somehow surprise the girl.

Leha asks for your help in calculating this expected value. Let this value be representable in the form of an irreducible fraction 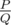. To further surprise Noora, he wants to name her the value .

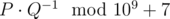Help Leha!

Input

The first line of input contains one integer number n (2 ≤ n ≤ 2·10⁵)  — number of vertices in a tree.

The second line contains n different numbers a₁, a₂, ..., a_n (1 ≤ a_i ≤ n) separated by spaces, denoting the values written on a tree vertices.

Each of the next n - 1 lines contains two integer numbers x and y (1 ≤ x, y ≤ n), describing the next edge of a tree. It is guaranteed that this set of edges describes a tree.

Output

In a single line print a number equal to P·Q^- 1 modulo 10⁹ + 7.

Examples

Input

Copy

3
1 2 3
1 2
2 3

Output

333333338

Input

Copy

5
5 4 3 1 2
3 5
1 2
4 3
2 5

Output

8

Note

Euler's totient function φ(n) is the number of such i that 1 ≤ i ≤ n,and gcd(i, n) = 1, where gcd(x, y) is the greatest common divisor of numbers x and y.

There are 6 variants of choosing vertices by Leha and Noora in the first testcase:

• u = 1, v = 2, f(1, 2) = φ(a₁·a₂)·d(1, 2) = φ(1·2)·1 = φ(2) = 1
• u = 2, v = 1, f(2, 1) = f(1, 2) = 1
• u = 1, v = 3, f(1, 3) = φ(a₁·a₃)·d(1, 3) = φ(1·3)·2 = 2φ(3) = 4
• u = 3, v = 1, f(3, 1) = f(1, 3) = 4
• u = 2, v = 3, f(2, 3) = φ(a₂·a₃)·d(2, 3) = φ(2·3)·1 = φ(6) = 2
• u = 3, v = 2, f(3, 2) = f(2, 3) = 2

Expected value equals to 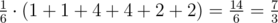. The value Leha wants to name Noora is 7·3^- 1 = 7·333333336 = 333333338 .

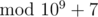In the second testcase expected value equals to 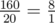, so Leha will have to surprise Hoora by number 8·1^- 1 = 8 .

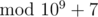$\varphi(a_i*a_j)=\frac{\varphi(a_i)\varphi(a_j)gcd(a_i,a_j)}{\varphi(gcd(a_i,a_j))}$
$\sum_{d=1}^{n}\frac{d}{\varphi(d)}\sum_{i=1}^{n}\sum_{j=1}^{n}\varphi(a_i)\varphi(a_j)dist(i,j)[gcd(a_i,a_j)=d]$
$f(d)=\sum_{i=1}^{n}\sum_{j=1}^{n}\varphi(a_i)\varphi(a_j)dist(i,j)[gcd(a_i,a_j)=d]$
$g(d)=\sum_{i=1}^{n}\sum_{j=1}^{n}\varphi(a_i)\varphi(a_j)dist(i,j)[d|gcd(a_i,a_j)]$
$g(d)=\sum_{d|x}^{n}f(x)$
$f(d)=\sum_{d|x}^{n}\mu(\frac{x}{d})g(x)$
$f(d)=\sum_{i=1}^{\frac{n}{d}}\mu(i)g(id)$
$ans=\sum_{d=1}^{n}\frac{d}{\varphi(d)}\sum_{i=1}^{\frac{n}{d}}\mu(i)g(id)$
令$T=id$
$ans=\sum_{T=1}^{n}g(T)\sum_{d|T}\mu(\frac{T}{d})\frac{d}{\varphi(d)}$
令$h(T)=\sum_{d|T}\mu(\frac{T}{d})\frac{d}{\varphi(d)}$
对于g(d)有
$g(d)=\sum_{i=1且d|a_i}^{n}\sum_{j=1 且d|a_j}^{n}\varphi(a_i)\varphi(a_j)(dep_i+dep_j-2*dep_lca)$
$g(d)=\sum_{i=1且d|a_i}^{n}\varphi(a_i)*2*dep_i\sum_{j=1 且d|a_j}^{n}\varphi(a_j)-2*\sum_{i=1且d|a_i}^{n}\sum_{j=1 且d|a_j}^{n}\varphi(a_i)\varphi(a_j)*dep_lca$
$\sum_{i=1且d|a_i}^{n}\varphi(a_i)*2*dep_i\sum_{j=1且d|a_j}^{n}\varphi(a_j)=2*\sum_{i=1且d|a_i}^{n}\varphi(a_i)*dep_i*Sum$

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long lol;
struct Node
{
  int next,to;
}edge[400001],edge2[400001];
int num,head[200001],head2[200001],mu[200001],phi[200001],vis[200001],inv[200001],Mod=1e9+7;
int n,tot,prime[200001],h[200001],dep[200001],fa[200001][21],dfn[200001],cnt,size[200001],st[400001];
int bin[21],ed[200001],flag[200001],ans,a[200001],sum,f[200001],l[400001],b[400001],top,g[200001];
int id[200001];
bool cmp(int a,int b)
{
  return dfn[a]<dfn[b];
}
void add(int u,int v)
{
  num++;
  edge[num].next=head[u];
  head[u]=num;
  edge[num].to=v;
}
void add2(int u,int v)
{
  num++;
  edge2[num].next=head2[u];
  head2[u]=num;
  edge2[num].to=v;
}
int qpow(int x,int y)
{
  int res=1;
  while (y)
    {
      if (y&1) res=1ll*res*x%Mod;
      x=1ll*x*x%Mod;
      y>>=1;
    }
  return res;
}
void prework()
{int i,j;
  mu[1]=phi[1]=1;
  inv[1]=1;
  for (i=2;i<=n;i++)
    inv[i]=1ll*(Mod-Mod/i)*inv[Mod%i]%Mod;
  for (i=2;i<=n;i++)
    {
      if (vis[i]==0)
    {
      ++tot;
      prime[tot]=i;
      mu[i]=-1;
      phi[i]=i-1;
    }
      for (j=1;j<=tot;j++)
    {
      if (1ll*i*prime[j]>n) break;
      vis[i*prime[j]]=1;
      if (i%prime[j]==0)
        {
          phi[i*prime[j]]=1ll*phi[i]*prime[j];
          break;
        }
      else
        {
          phi[i*prime[j]]=1ll*phi[i]*(prime[j]-1);
          mu[i*prime[j]]=-mu[i];
        }
    }
    }
  for (i=1;i<=n;i++)
    {
      for (j=1;j<=n&&1ll*i*j<=n;j++)
    {
      h[i*j]+=1ll*mu[j]*i%Mod*inv[phi[i]]%Mod;
      h[i*j]%=Mod;
    }
    }
}
int lca(int x,int y)
{int i;
  if (dep[x]<dep[y]) swap(x,y);
  for (i=20;i>=0;i--)
    if (dep[fa[x][i]]>=dep[y])
      x=fa[x][i];
  if (x==y) return x;
  for (i=20;i>=0;i--)
    {
      if (fa[x][i]!=fa[y][i])
    {
      x=fa[x][i];
      y=fa[y][i];
    }
    }
  return fa[x][0];
}
int get_dis(int x,int y)
{
  return dep[x]+dep[y]-2*dep[lca(x,y)];
}
void dfs(int x,int pa)
{int i;
  dep[x]=dep[pa]+1;
  dfn[x]=++cnt;
  size[x]=1;
  for (i=1;bin[i]<=dep[x];i++)
    fa[x][i]=fa[fa[x][i-1]][i-1];
  for (i=head[x];i;i=edge[i].next)
    {
      int v=edge[i].to;
      if (v==pa) continue;
      fa[v][0]=x;
      dfs(v,x);
      size[x]+=size[v];
    }
  ed[x]=cnt;
}
int DP(int x)
{
  int s1=0,s2=0;
  if (flag[x])
    {
      ans+=2ll*phi[a[x]]%Mod*sum%Mod*dep[x]%Mod;
      ans%=Mod;
      f[x]=phi[a[x]];
      s1=1ll*f[x]*f[x]%Mod*dep[x]%Mod;
    }
  else f[x]=0;
  for (int i=head2[x];i;i=edge2[i].next)
    {
      int v=edge2[i].to;
      DP(v);
      s2=(s2+1ll*f[x]*f[v]%Mod*dep[x]%Mod)%Mod;
      f[x]=(f[x]+f[v])%Mod;
    }
  ans=((ans-4ll*s2%Mod)%Mod-2ll*s1%Mod)%Mod;
  ans=(ans+Mod)%Mod;
}
void solve(int x)
{int i,Lca;
  int tot=0;sum=0;
  for (i=x;i<=n;i+=x)
    flag[l[++tot]=id[i]]=1,b[tot]=l[tot],sum=(sum+phi[i])%Mod;
  sort(l+1,l+tot+1,cmp);
  Lca=l[1];
  for (i=2;i<=tot;i++)
    if (ed[l[i-1]]<dfn[l[i]]) l[++tot]=lca(l[i],l[i-1]),Lca=lca(Lca,l[i]);
  l[++tot]=Lca;
  sort(l+1,l+tot+1,cmp);
  tot=unique(l+1,l+tot+1)-l-1;
  top=0;num=0;ans=0;
  st[++top]=Lca;
  for (i=2;i<=tot;i++)
    {
      while (top&&ed[st[top]]<dfn[l[i]]) top--;
      add2(st[top],l[i]);
      //cout<<x<<' '<<st[top]<<' '<<l[i]<<endl;
      st[++top]=l[i];
    }
  DP(Lca);
  g[x]=ans%Mod;
  for (i=1;i<=tot;i++) flag[l[i]]=0,head2[l[i]]=0;
}
int main()
{int i,j,u,v;
  cin>>n;
  bin[0]=1;
  for (i=1;i<=20;i++)
    bin[i]=bin[i-1]*2;
  prework();
  for (i=1;i<=n;i++)
    {
      scanf("%d",&a[i]);
      id[a[i]]=i;
    }
  for (i=1;i<=n-1;i++)
    {
      scanf("%d%d",&u,&v);
      add(u,v);add(v,u);
    }
  dfs(1,0);
  for (i=1;i<=n;i++)
    solve(i);
  ans=0;
  for (i=1;i<=n;i++)
    ans=(ans+1ll*g[i]*h[i]%Mod)%Mod;
  ans=1ll*ans*qpow(n-1,Mod-2)%Mod*qpow(n,Mod-2)%Mod;
  cout<<(ans+Mod)%Mod;
}

 

$\varphi(a_i*a_j)=\frac{\varphi(a_i)\varphi(a_j)gcd(a_i,a_j)}{\varphi(gcd(a_i,a_j))}$
$\sum_{d=1}^{n}\frac{d}{\varphi(d)}\sum_{i=1}^{n}\sum_{j=1}^{n}\varphi(a_i)\varphi(a_j)dist(i,j)[gcd(a_i,a_j)=d]$
$f(d)=\sum_{i=1}^{n}\sum_{j=1}^{n}\varphi(a_i)\varphi(a_j)dist(i,j)[gcd(a_i,a_j)=d]$
$g(d)=\sum_{i=1}^{n}\sum_{j=1}^{n}\varphi(a_i)\varphi(a_j)dist(i,j)[d|gcd(a_i,a_j)]$
$g(d)=\sum_{d|x}^{n}f(x)$
$f(d)=\sum_{d|x}^{n}\mu(\frac{x}{d})g(x)$
$f(d)=\sum_{i=1}^{\frac{n}{d}}\mu(i)g(id)$
$ans=\sum_{d=1}^{n}\frac{d}{\varphi(d)}\sum_{i=1}^{\frac{n}{d}}\mu(i)g(id)$
令$T=id$
$ans=\sum_{T=1}^{n}g(T)\sum_{d|T}\mu(\frac{T}{d})\frac{d}{\varphi(d)}$
令$h(T)=\sum_{d|T}\mu(\frac{T}{d})\frac{d}{\varphi(d)}$
对于g(d)有
$g(d)=\sum_{i=1且d|a_i}^{n}\sum_{j=1 且d|a_j}^{n}\varphi(a_i)\varphi(a_j)(dep_i+dep_j-2*dep_lca)$
$g(d)=\sum_{i=1且d|a_i}^{n}\varphi(a_i)*2*dep_i\sum_{j=1 且d|a_j}^{n}\varphi(a_j)-2*\sum_{i=1且d|a_i}^{n}\sum_{j=1 且d|a_j}^{n}\varphi(a_i)\varphi(a_j)*dep_lca$
$\sum_{i=1且d|a_i}^{n}\varphi(a_i)*2*dep_i\sum_{j=1且d|a_j}^{n}\varphi(a_j)=2*\sum_{i=1且d|a_i}^{n}\varphi(a_i)*dep_i*Sum$