SRM 558 SurroundingGame
题意:
给定一个网格,每个网格有选取代价和占据收益。每个点被占据,需要满足以下两个条件至少一个条件:1.被选取 2.邻近方格都被选取(有公共边被称为邻近) 不一定要占据所有方格,求最大收益。
输入说明
第一行两个数 n,m(n,m ≤ 20),表示矩形的长和宽。
接下来 n 行,每行是 m 个字符组成的字符串,描述投资的花费。
接下来 n 行,每行是 m 个字符组成的字符串,表示该格子的收益。
花费和收益按照一种奇葩的方式给出:
字符
数
‘0’-’9’
0-9
‘a’-’z’
10-35
‘A’-’Z’
36-61
输出说明
一个数,表示收益的和减去投资的和的最大值。
样例 1
2 2
21
12
21
12
答案:4
样例 2
2 2
ZZ
ZZ
11
11
答案: 0
样例 3
3 3
XXX
XXX
XXX
aaa
aZa
aaa
答案: 2
样例 4
2 4
asam
atik
123A
45BC
答案: 71
样例 5
98
IIIIIIII
IIWWWWII
IIWIIIII
IIWIIIII
IIWWWWII
IIIIIWII
IIIIIWII
IIWWWWII
IIIIIIII
IIIIIIII
II0000II
II0II0II
II0II0II
II0000II
II0II0II
II0II0II
II0000II
IIIIIIII
答案: 606
先黑白染色
源点S点连白点,汇点T点连黑点
现将所有利润加起来,显然要减去一部分花费和利润
我们求最小的使利润合法的要减去一部分花费和利润
然后转化为求最小割,设收益边和花费边
首先考虑几种情况
1.保留一个点的花费边,保留收益边(即不投资拿到利润)
那么此刻如果相邻有点没有割掉花费边,那么就会有流
2.割掉一个花费边,保留收益边(投资一个点)
3.割掉一个收益边,保留花费边(不投资该点)
只考虑前2中情况我们可以建出:
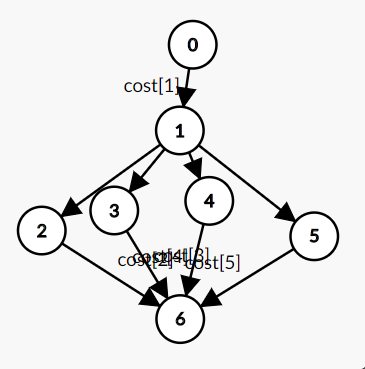
考虑第3种情况:
因为放弃这个格子的收益,代表着相邻的格子的收益必须要靠它自己的花费
于是有了如下建图

图片转自ZYYS
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #include<queue> 7 using namespace std; 8 struct Node 9 { 10 int next,to,cap; 11 }edge[200001]; 12 int head[6001],num=1,inf=1e9,S,T,dist[6001],n,m,a[51][51],b[51][51],ans,tot,pre[51][51],nxt[51][51],col[51][51]; 13 char s1[51][51],s2[51][51]; 14 void add(int u,int v,int cap) 15 { 16 num++; 17 edge[num].next=head[u]; 18 head[u]=num; 19 edge[num].to=v; 20 edge[num].cap=cap; 21 num++; 22 edge[num].next=head[v]; 23 head[v]=num; 24 edge[num].to=u; 25 edge[num].cap=0; 26 } 27 bool bfs() 28 {int i; 29 queue<int>Q; 30 for (i=S;i<=T;i++) 31 dist[i]=-1; 32 dist[S]=0; 33 Q.push(S); 34 while (Q.empty()==0) 35 { 36 int u=Q.front(); 37 Q.pop(); 38 for (i=head[u];i;i=edge[i].next) 39 { 40 int v=edge[i].to; 41 if (edge[i].cap==0||dist[v]!=-1) continue; 42 dist[v]=dist[u]+1; 43 Q.push(v); 44 } 45 } 46 if (dist[T]==-1) return 0; 47 return 1; 48 } 49 int dfs(int x,int flow,int des) 50 {int i; 51 if (x==des) return flow; 52 if (flow<=0) return 0; 53 int res=0,tmp; 54 for (i=head[x];i;i=edge[i].next) 55 { 56 int v=edge[i].to; 57 if (dist[v]==dist[x]+1&&edge[i].cap) 58 { 59 tmp=dfs(v,min(edge[i].cap,flow-res),des); 60 edge[i].cap-=tmp; 61 edge[i^1].cap+=tmp; 62 res+=tmp; 63 if (res==flow) return res; 64 } 65 } 66 return res; 67 } 68 int Maxflow() 69 { 70 int as=0; 71 while (bfs()) 72 { 73 int a=0; 74 while (a=dfs(S,inf,T)) as+=a; 75 } 76 return as; 77 } 78 int main() 79 {int i,j; 80 cin>>n>>m; 81 for (i=0;i<n;i++) 82 { 83 scanf("%s",s1[i]); 84 } 85 for (i=0;i<n;i++) 86 { 87 scanf("%s",s2[i]); 88 } 89 for (i=1;i<=n;i++) 90 { 91 for (j=1;j<=m;j++) 92 { 93 if (s1[i-1][j-1]>='0'&&s1[i-1][j-1]<='9') 94 a[i][j]=s1[i-1][j-1]-'0'; 95 else if (s1[i-1][j-1]>='a'&&s1[i-1][j-1]<='z') 96 a[i][j]=s1[i-1][j-1]-'a'+10; 97 else a[i][j]=s1[i-1][j-1]-'A'+36; 98 } 99 } 100 for (i=1;i<=n;i++) 101 { 102 for (j=1;j<=m;j++) 103 { 104 if (s2[i-1][j-1]>='0'&&s2[i-1][j-1]<='9') 105 b[i][j]=s2[i-1][j-1]-'0'; 106 else if (s2[i-1][j-1]>='a'&&s2[i-1][j-1]<='z') 107 b[i][j]=s2[i-1][j-1]-'a'+10; 108 else b[i][j]=s2[i-1][j-1]-'A'+36; 109 ans+=b[i][j]; 110 } 111 } 112 S=1;tot=1; 113 for (i=1;i<=n;i++) 114 { 115 for (j=1;j<=m;j++) 116 { 117 pre[i][j]=++tot;nxt[i][j]=++tot; 118 col[i][j]=(i+j)&1; 119 } 120 } 121 T=++tot; 122 for (i=1;i<=n;i++) 123 { 124 for (j=1;j<=m;j++) 125 { 126 if (col[i][j]==0) 127 { 128 add(S,pre[i][j],a[i][j]); 129 add(pre[i][j],nxt[i][j],b[i][j]); 130 if (i-1) 131 add(pre[i][j],nxt[i-1][j],inf),add(nxt[i][j],pre[i-1][j],inf); 132 if (i<n) 133 add(pre[i][j],nxt[i+1][j],inf),add(nxt[i][j],pre[i+1][j],inf); 134 if (j-1) 135 add(pre[i][j],nxt[i][j-1],inf),add(nxt[i][j],pre[i][j-1],inf); 136 if (j<m) 137 add(pre[i][j],nxt[i][j+1],inf),add(nxt[i][j],pre[i][j+1],inf); 138 } 139 else 140 { 141 add(pre[i][j],T,a[i][j]); 142 add(nxt[i][j],pre[i][j],b[i][j]); 143 } 144 } 145 } 146 cout<<ans-Maxflow(); 147 }


