数列

题目描述
数列{xn}的递推公式如下:
给定 x 0 , a, b, c, n, m,求 x n mod m 的值。
输入格式
一行,六个整数,分别表示 x 0 , a, b, c, n, m。
输出格式
一行,一个整数,表示 x n mod m 的值。
输入样例
1 1 1 1 5 1000000000
输出样例
133904603

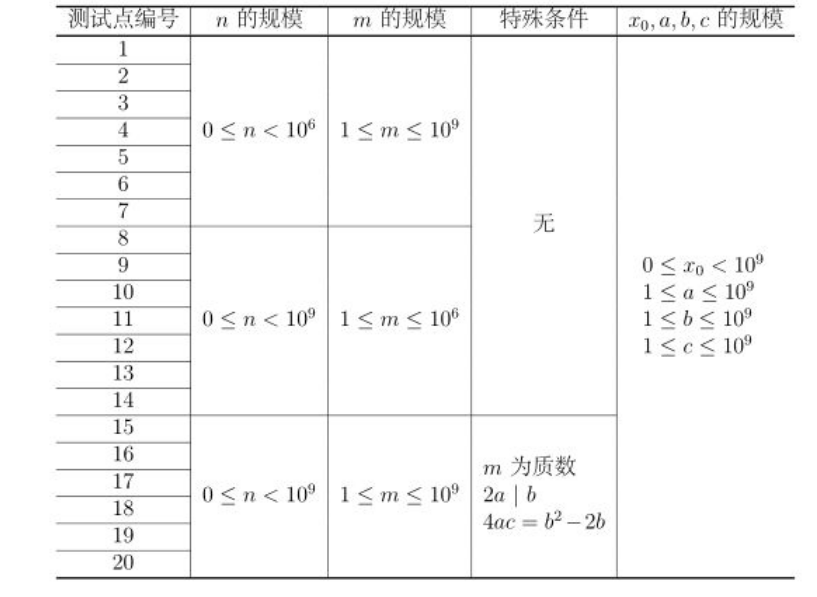
数据规模与约定

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<cmath>
 6 using namespace std;
 7 typedef long long lol;
 8 lol a,b,c,n,Mod,x,now,last,f[1000001],st,len,ans;
 9 lol qpow(lol x,lol y,lol p)
10 {
11   lol res=1;
12   while (y)
13     {
14       if (y&1) res=res*x%p;
15       x=x*x%p;
16       y>>=1;
17     }
18   return res;
19 }
20 int vis[1000001];
21 int main()
22 {
23     int i;
24     lol p,inv;
25     cin>>x>>a>>b>>c>>n>>Mod;
26     memset(vis,-1,sizeof(vis));
27     if (n<=1000000)
28     {
29         x%=Mod;
30         last=x;
31         for (i=1; i<=n; i++)
32         {
33             now=(a*last%Mod*last%Mod+b*last%Mod)%Mod+c;
34             now%=Mod;
35             last=now;
36         }
37         cout<<last;
38     }
39     else if (Mod<=10000000)
40     {
41         x%=Mod;
42         last=x;
43         vis[x]=0;
44         f[0]=x;
45         for (i=1; i; i++)
46         {
47             now=(a*last%Mod*last%Mod+b*last%Mod)%Mod+c;
48             now%=Mod;
49             last=now;
50             f[i]=now;
51             if (vis[now]!=-1) break;
52             vis[now]=i;
53         }
54         st=vis[f[i]];
55         len=i-st;
56         while (n>=i)
57         {
58             n-=len;
59         }
60         cout<<f[n];
61     }
62     else
63       {
64     p=qpow(2,n,Mod-1);
65     inv=qpow(2*a,Mod-2,Mod);
66     now=a*((x+b*inv%Mod)%Mod)%Mod;
67     ans=qpow(now,p,Mod);
68     ans=(ans*qpow(a,Mod-2,Mod)%Mod-b*inv%Mod+Mod)%Mod;
69     cout<<ans;
70       }
71 }

 

posted @ 2018-03-20 16:46  Z-Y-Y-S  阅读(306)  评论(0)  编辑  收藏  举报