[HNOI2012]与非
题目描述
NAND(与非)是一种二元逻辑运算,其运算结果为真当且仅当两个输入的布尔值不全为真。NAND运算的真值表如下(1表示真,0表示假):
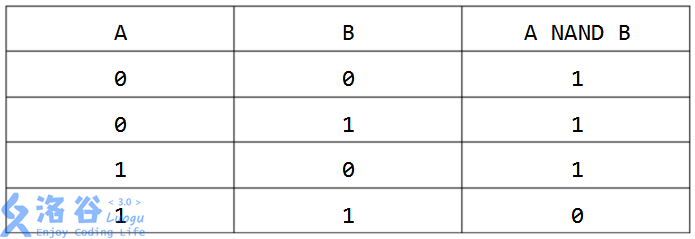
两个非负整数的NAND是指将它们表示成二进制数,再在对应的二进制位进行NAND运算。由于两个二进制数的长度可能不等,因此一般约定一个最高位K,使得两个数的二进制表示都不 超过K位,不足K位的在高位补零。给定N个非负整数A1,A2......AN和约定位数K,利用NAND运算与括号,每个数可以使用任意次,请你求出范围[L,R]内可以被计算出的数有多少个。
输入输出格式
输入格式:
输入文件第一行是用空格隔开的四个正整数N,K,L和R,接下来的一行是N个非负整数A1,A2......AN,其含义如上所述。 100%的数据满足K<=60且N<=1000,0<=Ai<=2^k-1,0<=L<=R<=10^18
输出格式:
仅包含一个整数,表示[L,R]内可以被计算出的数的个数
输入输出样例
说明
样例1中,(3 NAND 4) NADN (3 NAND 5) = 1,5 NAND 5 = 2,3和4直接可得。
可以表示出其他所有的位运算
$not\ A=A\ nand\ A$
$A\ and\ B=not\ (A\ nand\ B)$
$A\ or\ B=(not\ A)\ nand\ (not\ B)$
$A\ xor\ B=(A\ and\ not\ B)\ or\ (not\ A\ and\ B)$
所以相当于是这$n$ 个数之间可以做任何位运算。
如果这$n$ 个数中每个数的第$i$ 位和第$j$ 位都相同,那么这$n$ 个数无论怎么运算,最后得到的答案中第$i$ 位和第$j$ 位一定相同
然后就是数位dp
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 typedef long long lol; 8 lol tmp[81],c[81],cnt[81],Q[81][81]; 9 lol a[2001],k,n,L,R; 10 lol dfs(lol s,lol x,lol flag) 11 {lol i,j; 12 if (x<0) return 1; 13 if (!flag) 14 { 15 memcpy(tmp,c,sizeof(c)); 16 lol tot=0; 17 for (i=x;i>=0;i--) 18 if (tmp[i]==-1) 19 { 20 tot++; 21 for (j=0;j<=cnt[i];j++) 22 { 23 tmp[Q[i][j]]=1; 24 } 25 } 26 return 1ll<<tot; 27 } 28 lol ed=((s>>x)&1); 29 lol sum=0; 30 if (c[x]==-1) 31 { 32 for (i=0;i<=ed;i++) 33 { 34 for (j=0;j<=cnt[x];j++) 35 { 36 c[Q[x][j]]=i; 37 } 38 sum+=dfs(s,x-1,flag&(i==ed)); 39 } 40 for (j=0;j<=cnt[x];j++) 41 { 42 c[Q[x][j]]=-1; 43 } 44 return sum; 45 } 46 else 47 { 48 if (flag&&c[x]&&ed==0) return 0; 49 return dfs(s,x-1,flag&(c[x]==ed)); 50 } 51 } 52 lol solve(lol s) 53 { 54 memset(c,-1,sizeof(c)); 55 if (s<0) return 0; 56 return dfs(s,k-1,(s>>k)?0:1); 57 } 58 int main() 59 {lol i,j,l,flag; 60 cin>>n>>k>>L>>R; 61 for (i=1;i<=n;i++) 62 scanf("%lld",&a[i]); 63 for (i=k-1;i>=1;i--) 64 { 65 for (j=i-1;j>=0;j--) 66 { 67 flag=0; 68 for (l=1;l<=n;l++) 69 if (((a[l]>>i)&1)^((a[l]>>j)&1)) 70 { 71 flag=1;break; 72 } 73 if (flag==0) 74 Q[i][++cnt[i]]=j; 75 } 76 Q[i][0]=i; 77 } 78 printf("%lld\n",solve(R)-solve(L-1)); 79 }

