Round Numbers

Description

The cows, as you know, have no fingers or thumbs and thus are unable to play Scissors, Paper, Stone' (also known as 'Rock, Paper, Scissors', 'Ro, Sham, Bo', and a host of other names) in order to make arbitrary decisions such as who gets to be milked first. They can't even flip a coin because it's so hard to toss using hooves.

They have thus resorted to "round number" matching. The first cow picks an integer less than two billion. The second cow does the same. If the numbers are both "round numbers", the first cow wins,
otherwise the second cow wins.

A positive integer N is said to be a "round number" if the binary representation of N has as many or more zeroes than it has ones. For example, the integer 9, when written in binary form, is 1001. 1001 has two zeroes and two ones; thus, 9 is a round number. The integer 26 is 11010 in binary; since it has two zeroes and three ones, it is not a round number.

Obviously, it takes cows a while to convert numbers to binary, so the winner takes a while to determine. Bessie wants to cheat and thinks she can do that if she knows how many "round numbers" are in a given range.

Help her by writing a program that tells how many round numbers appear in the inclusive range given by the input (1 ≤ Start < Finish ≤ 2,000,000,000).

Input

Line 1: Two space-separated integers, respectively Start and Finish.

Output

Line 1: A single integer that is the count of round numbers in the inclusive range Start..Finish

Sample Input

2 12

Sample Output

6

 

要知道闭区间 [a ,b] 内有多少个Round number，只需要分别求出

闭区间 [0 ,a] 内有T个RN

闭区间 [0 ,b+1] 内有S个RN

再用 S – T 就是闭区间 [a ,b] 内的RN数了

至于为什么是 b+1，因为对于闭区间 [0 ,k] ，我下面要说的算法求出的是比k小的RN数，就是说不管 k是不是RN, 都没有被计算在内，所以若要把闭区间[a ,b]的边界a和b都计算在内，就要用上述的处理方法。

现在问题的关键就是如何求[0 ,k]内的RN数了

首先要把k转化为二进制数bin-k，并记录其位数（长度）len

那么首先计算长度小于len的RN数有多少（由于这些数长度小于len，那么他们的值一定小于k，因此在进行组合时就无需考虑组合所得的数与k之间的大小了）

for(i=1;i<bin[0]-1;i++)         //bin[0]记录的是二进制数的长度len
              for(j=i/2+1;j<=i;j++)
                     sum+=c[i][j];

可以看到，i<len-1 ，之所以减1，是因为这些长度比len小的数，最高位一定是1，那么剩下可供放入数字的位数就要再减少一个了

这条程序得到的sum为

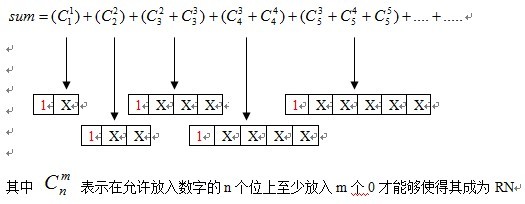
1表示当前处理的二进制数的最高位，X表示该二进制数待放入数字的位

显然这段程序把  二进制数0  排除在外了，这个是最终结果没有影响的，因为最后要把区间[a , b]首尾相减，0存不存在都一样了。

然后计算长度等于len的RN数有多少（由于这些数长度等于len，那么他们的值可能小于k，可能大于k，因此在进行组合时就要考虑组合所得的数与k之间的大小了）

int zero=0;  //从高位向低位搜索过程中出现0的位的个数
       for(i=bin[0]-1;i>=1;i--)
              if(bin[i])   //当前位为1
                     for(j=(bin[0]+1)/2-(zero+1);j<=i-1;j++)
                            sum+=c[i-1][j];
              else
                     zero++;

之所以初始化i=bin[0]-1，是因为bin[]是逆向存放k的二进制的，因此要从高位向低位搜索，就要从bin[]后面开始，而要 bin[0]-1 ，是因为默认以后组合的数长度为len，且最高位为1，因此最高位不再搜索了。

那么问题的关键就是怎样使得以后组合的数小于k了

这个很简单：

从高位到低位搜索过程中，遇到当前位为0，则不处理，但要用计数器zero累计当前0出现的次数

遇到当前位为1，则先把它看做为0，zero+1，那么此时当前位 后面的 所有低位任意组合都会比k小，找出这些组合中RN的个数，统计完毕后把当前位恢复为原来的1，然后zero-1，继续向低位搜索

那么问题就剩下 当当前位为1时，把它看做0之后，怎样去组合后面的数了

此时组合要考虑2个方面：

（1）       当前位置i后面允许组合的低位有多少个，我的程序由于bin是从bin[1]开始存储二进制数的，因此 当前位置i后面允许组合的低位有i-1个

（2）       组合前必须要除去前面已出现的0的个数zero

我的程序中初始化j=(bin[0]+1)/2-(zero+1)， j本来初始化为(bin[0]+1)/2就可以了，表示对于长度为bin[0]的二进制数，当其长度为偶数时，至少其长度一半的位数为0，它才是RN，当其长度为奇数时，至少其长度一半+1的位数为0，它才是RN。

但是现在还必须考虑前面出现了多少个0，根据前面出现的0的个数，j的至少取值会相应地减少。  -(zero+1) ，之所以+1，是因为要把当前位bin[i]看做0

可能有疑问，为什么不能在前面1改0的情况下把0改1？

因为在之前1改0时，排列组合低位已经包含了这种情况，所以0改1可以忽略

这题启示我们遇到这种与二进制或位数有关的题可以枚举位来组合(有数位dp的思想)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
long long c[33][33],ans;
int bin[51];
int binary(int x)
{int len=0;
  memset(bin,0,sizeof(bin));
  while (x)
    {
      bin[++len]=x%2;
      x/=2;
    }
  return len;
}
long long count(int x)
{int i,j,zero=0;
  int len=binary(x);
  ans=0;
  for (i=1;i<len-1;i++)
    for (j=i/2+1;j<=i;j++)
      ans+=c[i][j];
  for (i=len-1;i>=1;i--)
    if (bin[i]==1)
      {
    for (j=(len+1)/2-(zero+1);j<=i-1;j++)
      ans+=c[i-1][j];
      }
    else zero++;
  return ans;
}
int main()
{int i,j,a,b;
  c[0][0]=1;
  for (i=1;i<=32;i++)
    {
      c[i][0]=1;
      for (j=1;j<=i;j++)
    {
      c[i][j]=c[i-1][j-1]+c[i-1][j];
    }
    }
  cin>>a>>b;
  cout<<count(b+1)-count(a);
}