车的放置
题目描述
有下面这样的一个网格棋盘,a,b,c,d表示了对应边长度,也就是对应格子数。
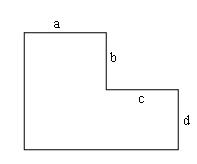
当a=b=c=d=2时,对应下面这样一个棋盘
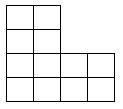
要在这个棋盘上放K个相互不攻击的车,也就是这K个车没有两个车在同一行,也没有两个车在同一列,问有多少种方案。同样只需要输出答案mod 100003后的结果。
输入输出格式
输入格式:
输入文件place.in的第1行为有5个非负整数a, b, c, d和k。
输出格式:
输出文件place.out包括1个正整数,为答案mod 100003后的结果。
输入输出样例
说明
【数据规模与约定】
对于部分数据,有b = 0;
对于部分数据,有a,b,c,d≤4。
对于100%的数据,a,b,c,d,k≤1000,且保证了至少有一种可行方案。
把图形左右翻转
令f[i][j]为前j列,放了i个车的方案,v[j]为第j列的高度
f[i][j]=f[i][j-1]+f[i-1][j-1]*(v[j]-i+1)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 int Mod=100003; 7 int a,b,c,d,k; 8 long long f[1001][2001],v[2001]; 9 int main() 10 {int i,j; 11 cin>>a>>b>>c>>d>>k; 12 for (i=1;i<=c;i++) 13 v[i]=d,f[0][i]=1; 14 for (i=c+1;i<=a+c;i++) 15 v[i]=b+d,f[0][i]=1; 16 f[0][0]=1; 17 for (j=1;j<=a+c;j++) 18 for (i=1;i<=k;i++) 19 f[i][j]=(f[i][j-1]+f[i-1][j-1]*(v[j]-i+1))%Mod; 20 cout<<f[k][a+c]; 21 }


