将军令

题目背景

pdf题面和大样例链接：http://pan.baidu.com/s/1cawM7c 密码：xgxv

 历史/落在/赢家/之手 
 至少/我们/拥有/传说 
 谁说/败者/无法/不朽 
 拳头/只能/让人/低头 
 念头/却能/让人/抬头 
 抬头/去看/去爱/去追 
 你心中的梦

题目描述

又想起了四月。

如果不是省选，大家大概不会这么轻易地分道扬镳吧？ 只见一个又一个昔日的队友离开了机房。

凭君莫话封侯事，一将功成万骨枯。

梦里，小 F 成了一个给将军送密信的信使。

现在，有两封关乎国家生死的密信需要送到前线大将军帐下，路途凶险，时间紧迫。小 F 不因为自己的祸福而避趋之，勇敢地承担了这个任务。

不过，小 F 实在是太粗心了，他一不小心把两封密信中的一封给弄掉了。

小 F 偷偷打开了剩下的那封密信。他 发现一副十分详细的地图，以及几句批文——原来 这是战场周围的情报地图。他仔细看后发现，在这张地图上标记了 n 个从 1 到 n 标号的 驿站，n − 1 条长度为 1 里的小道，每条小道双向连接两个不同的驿站，并且驿站之间可以 通过小道两两可达。

小 F 仔细辨认着上面的批注，突然明白了丢失的信的内容了。原来，每个驿站都可以驻 扎一个小队，每个小队可以控制距离不超过 k 里的驿站。如果有驿站没被控制，就容易产 生危险——因此这种情况应该完全避免。而那封丢失的密信里，就装着朝廷数学重臣留下的 精妙的排布方案，也就是用了最少的小队来控制所有驿站。

小 F 知道，如果能计算出最优方案的话，也许他就能够将功赎过，免于死罪。他找到了 你，你能帮帮他吗？ 当然，小 F 在等待你的支援的过程中，也许已经从图上观察出了一些可能会比较有用的 性质，他会通过一种特殊的方式告诉你。

输入输出格式

输入格式：

从标准输入中读入数据。

输入第 1 行一个正整数 n,k,t，代表驿站数，一支小队能够控制的最远距离，以及特 殊性质所代表的编号。关于特殊性质请参照数据范围。

输入第 2 行至第 n 行，每行两个正整数 uiu_iui​,viv_ivi​，表示在 uiu_iui​ 和 viv_ivi​ 间，有一条长度为 一里的小道。

输出格式：

输出到标准输出中。

输出一行，为最优方案下需要的小队数。

输入输出样例

输入样例#1： 复制 
4 1 0 
1 2 
1 3 
1 4
输出样例#1： 复制 
1
输入样例#2： 复制 
6 1 0 
1 2 
1 3 
1 4 
4 5 
4 6
输出样例#2： 复制 
2

说明

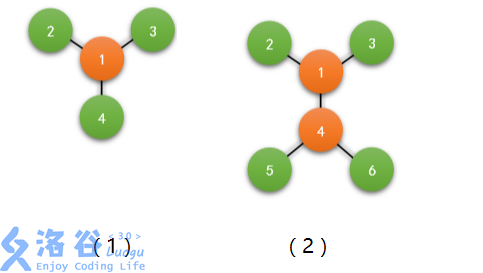
【样例 1 说明】

如图。由于一号节点到周围的点距离均是 1，因此可以控制所有驿站。

【样例 2 说明】

如图，和样例 1 类似。

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

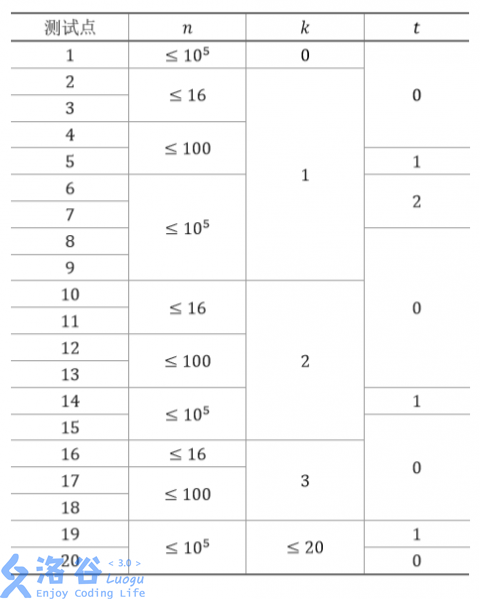
关于 t 的含义如下： t = 0：该测试点没有额外的特殊性质； t = 1：保证最多 8 个点的所连接的小道超过 1 条； t = 2：保证所有点到 1 号点的距离不超过 2。

每个测试点的数据规模及特点如下表

此题和HNOI2003消防局的设立很像

不过原题只覆盖距离为2

所以这题dp会很不好做

因为当前最深的点肯定需要覆盖

所以贪心，越靠近祖先越好，直接放在距离为k的祖先上

很明显，越往根走深度越小随之管辖的范围也越大，可以波及许多地方，而越往边上的是最难管的。所以和疫情控制一样预处理时需要处理出深度，父亲节点。

然后把与管辖站距离为k的距离的点标记可达，之后再在未标记的点中选一个

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 struct Node
 7 {
 8   int next,to;
 9 }edge[200001];
10 struct FFF
11 {
12   int x,d;
13   bool p;
14 }a[100001];
15 int head[100001],num,n,k,t,fa[100001],dep[100001],cnt,id[100001],ans;
16 bool cmp(FFF a,FFF b)
17 {
18   return a.d>b.d;
19 }
20 void add(int u,int v)
21 {
22   num++;
23   edge[num].next=head[u];
24   head[u]=num;
25   edge[num].to=v;
26 }
27 void dfs(int x,int pa)
28 {int i;
29   fa[x]=pa;
30   dep[x]=dep[pa]+1;
31   a[++cnt].d=dep[x];
32   a[cnt].x=x;
33   a[cnt].p=0;
34   for (i=head[x];i;i=edge[i].next)
35     {
36       int v=edge[i].to;
37       if (v!=pa)
38     {
39       dfs(v,x);
40     }
41     }
42 }
43 void take(int x,int pre,int s)
44 {int i;
45   a[id[x]].p=1;
46   if (s>k) return;
47   for (i=head[x];i;i=edge[i].next)
48     {
49       int v=edge[i].to;
50       if (v!=pre) 
51     {
52       take(v,x,s+1);
53     }
54     }
55 }
56 int main()
57 {int i,u,v,j;
58   cin>>n>>k>>t;
59   for (i=1;i<=n-1;i++)
60     {
61       scanf("%d%d",&u,&v);
62       add(u,v);add(v,u);
63     }
64   dfs(1,1);
65   sort(a+1,a+n+1,cmp);
66   for (i=1;i<=n;i++)
67     id[a[i].x]=i;
68   for (i=1;i<=n;i++)
69     if (a[i].p==0)
70       {
71       ans++;
72       int x=a[i].x;
73       for (j=1;j<=k;j++)
74     if (fa[x]) x=fa[x];
75       take(x,0,1);
76     }
77   cout<<ans;
78 }

 

posted @ 2017-11-03 15:57  Z-Y-Y-S  阅读(255)  评论(0)  编辑  收藏  举报