友好的生物

【问题描述】
W 星球是一个和地球一样气候适宜、物种聚集的星球。经过多年的研究,外星生物学
家们已经发现了数万种生物,而且这个数字还在不断增大。
W 星球上的生物很有趣,有些生物之间很友好,朝夕相伴,形影不离;但有些却很敌
对,一见面就难免发生战斗。为了能够更好地了解它们之间的友好程度,外星生物学家希望
进行一些量化的计算。他们发现,两种生物之间的友好程度和它们的 K 种属性有关,暂且将
它们编号为属性 1、属性 2、......、属性 K,这些属性都是可以进行量化的。外星生物学家
研究发现,如果前 K-1 种属性的差别越大,这两种生物就越友好;但是属性 K 与众不同,这
种属性差别越小的两种生物越友好。
因此他们猜想是不是可以用这样一个公式量化两种生物之间的友好程度:

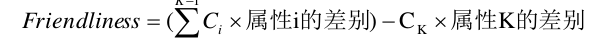
,其中 Ci 是非负常数。如果
知道了每种生物的各种属性,利用上述公式就很容易算出它们之间的友好程度了。现在,外
星生物学家们想问一问:在目前发现的这些生物当中,关系最友好的那对生物是哪一对呢?
它们之间的友好程度是多少?
【输入文件】
输入文件的第一行是两个整数 N 和 K,分别表示目前发现的生物种数和属性的种数。
第二行有 K 个非负整数 Ci,即计算友好程度时所需的常数。
接下来的 N 行,描述每种生物,按照先后顺序依次编号为生物 1、生物 2、......、生物 N。
每一行都有 K 个整数,给出该种生物的各项属性值,按照先后顺序依次编号为属性 1、属性
2、......、属性 K。
【输出文件】
输出文件包含一行,为一个整数,表示最友好的生物之间的友好程度。
【约定】
2 ≤ N ≤ 100,000
2 ≤ K ≤ 5
0 ≤ Ci ≤ 100。
每种生物的各项属性值不小于-10000 且不大于 10000
最大的友好程度一定大于 0
【样例输入】
5 3
1 2 3
-5 3 2
-2 3 0
0 5 9
3 4 -1
-10 -11 7
【样例输出】
36

对于|a-b|,只有两种情况

a-b       （a>b）

-a+b     （a<=b）

对于两个动物i，j 　　k=4

可以写成(a[i][1]-a[i][2]+a[i][3]-a[i][4])-(a[j][1]-a[j][2]+a[j][3]-a[j][4])

以上是满足(a[i][1]>a[j][1],a[i][2]<a[j][2],a[i][3]>a[j][3],a[i][4]>a[j][4])时的式子

现在唯一有问题就是两两之间大小关系不确定

其实发现可以忽略大小关系，去看符号关系(比如上面就是+-+-)

以上面(i,j)举例，如果用它去对应两种符号关系，那么肯定是正确的最大

因为不正确的符号关系肯定会有一项小于0，所以会比正确的小

于是我们用搜索构出所有符号关系O(2^k)，再用这个关系去O(nk)求一个最大值

令F[i]=(a[i][1]?a[i][2]?a[i][3]?a[i][4]?a[i][5])

那么最大值就是max(F[1~i-1]-F[i])

因为第k位是特殊的，这里特殊处理(也是因为再枚举第k位会超时)：

符号直接赋为+

事先将动物按第k属性从小到大排序

这样就满足条件了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
struct FFF
{
  int a[6];
}a[100001];
int n,k,b[6],ans,c[6];
bool cmp(FFF a,FFF b)
{
  return a.a[k]<b.a[k];
}
void check()
{int i,j;
  int maxn=0,tmp=0;
  for (i=1;i<=k;i++)
    tmp+=a[1].a[i]*b[i];
  maxn=tmp;
  for (i=2;i<=n;i++)
    {tmp=0;
      for (j=1;j<=k;j++)
    tmp+=a[i].a[j]*b[j];
      ans=max(ans,maxn-tmp);
      maxn=max(maxn,tmp);
    }
}
void dfs(int x)
{
  if (x==k)
    {
      b[x]=1;
      check();
      return;
    }
  b[x]=1;dfs(x+1);
  b[x]=-1;dfs(x+1);
}
int main()
{int i,j;
  cin>>n>>k;
  for (i=1;i<=k;i++)
    scanf("%d",&c[i]);
  for (i=1;i<=n;i++)
    {
      for (j=1;j<=k;j++)
    scanf("%d",&a[i].a[j]),a[i].a[j]*=c[j];
    }
  sort(a+1,a+n+1,cmp);
  dfs(1);
  cout<<ans;
}