基因重组
1s / 32M
【问题描述】
目前,科学家们正致力于对生物基因的重组进行深入研究。基因的物质载体是脱氧核糖
核酸(DNA)
。DNA 是一种仅由 A、T、G、C 四种基元构成的双螺旋结构的有机分子。
DNA 的两条单链上,同一位置的两个基元是互相对应的。A 对 T,G 对 C,因此,我们
只需用任意一条链上的基元排列,就可以表示 DNA 的分子结构。例如:ATTGAGCCGTAT。
由于 DNA 微小而复杂,重组 DNA 极其困难,科学家们打算利用一条现成的 DNA 链作原
材料拼接成另外一条新的 DNA 链。即使这样,拼接 DNA 仍然是一件繁重的工作,非人力所
能胜任。所以科学家们制造了一种手术机器人 TuringM 来完成这项任务。TuringM 每次只能
在目标链(T)的右端与原材料 (S) 的左端进行操作。它有下列几种基本拼接操作:
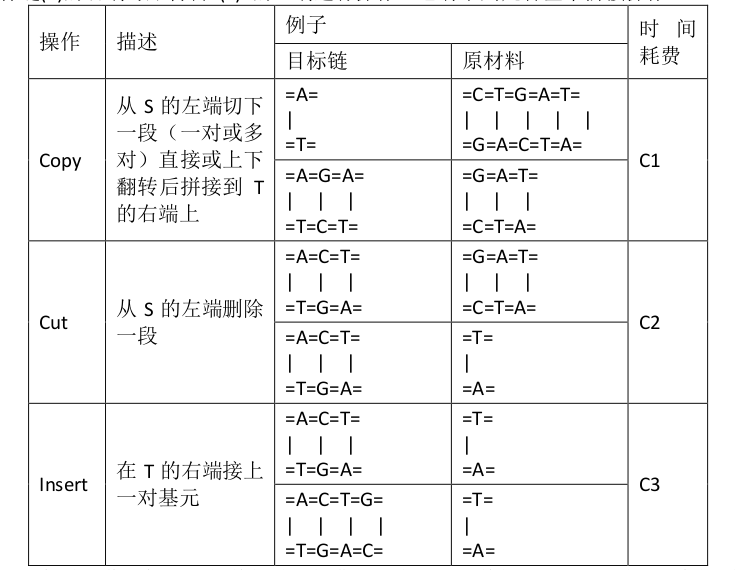
对于每种操作,机器人的单位时间耗费如上表所示(单位:分钟)
。最后剩余的原材料
自动丢弃。现在的任务是请你编一个程序,帮助科学家们找出完成 DNA 链拼接的最少时间。
从 S 的左端切下
一段(一对或多
对)直接或上下
翻转后拼接到 T
的右端上
【输入格式】
输入文件包括三行,第一行是三个数 c1、c2、c3。
二、三两行每行一个字符串,分别表示原材料 DNA 与目标 DNA 链的上半部分。
【输出格式】
输出文件只有一行,表示拼接出目标 DNA 的最小时间。
【输入输出样例】
3 2 3
CCGATGTATCTG
TACGATCGGTC
输出
23
【数据规模】
DNA 链的长度不超过 5000
最少时间不会超过 10 天。
令f[i][j][0/1]表示原材料消除j个,目标构成i个
最后一次是1操作(0/1对应正反)
f[i][j][2]表示最后一次是2操作
f[i][j][3]表示最后一次是3操作
于是有:
f[i+1][j][3]=min(f[i][j][0~3])+c3 (给结果材料加一位)
f[i][j+1][2]=min(f[i][j][2],min(f[i][j][0,1,3])+c2)
(删掉一位原材料,前一个表示把这次操作和上一个2操作合并)
f[i+1][j+1][0/1]=min(f[i][j][0/1],min(f[i][j][0~3])+c1)
(表示删掉一位原材料,加入结果材料,要求必须原材料j位和目标材料i位要匹配)
初始化直接f[0][0][3]就行了,因为3操作只能加一位,不能与前面的3合并
所以就相当于初始无操作
内存不够,要滚动数组
%%%%%%YZD巨佬
1 #include<iostream> 2 #include<cstring> 3 #include<algorithm> 4 #include<cstdio> 5 #include<cmath> 6 using namespace std; 7 int a1[5005],a2[5005],f[2][5005][5],c1,c2,c3,now,nxt,n,m,inf,ans; 8 char s[5005]; 9 int main() 10 {int i,j; 11 cin>>c1>>c2>>c3; 12 cin>>s; 13 m=strlen(s); 14 for (i=0;i<m;i++) 15 if (s[i]=='A') a1[i+1]=0; 16 else if (s[i]=='T') a1[i+1]=1; 17 else if (s[i]=='C') a1[i+1]=2; 18 else if (s[i]=='G') a1[i+1]=3; 19 cin>>s; 20 n=strlen(s); 21 for (i=0;i<n;i++) 22 if (s[i]=='A') a2[i+1]=0; 23 else if (s[i]=='T') a2[i+1]=1; 24 else if (s[i]=='C') a2[i+1]=2; 25 else if (s[i]=='G') a2[i+1]=3; 26 now=0;nxt=1; 27 memset(f,127/3,sizeof(f)); 28 inf=f[0][0][0]; 29 f[0][0][3]=0; 30 now=0;nxt=1; 31 for (i=0;i<n;i++) 32 { 33 for (j=0;j<=m;j++) 34 { 35 f[nxt][j][3]=min(f[nxt][j][3],min(min(f[now][j][0],f[now][j][1]),min(f[now][j][2],f[now][j][3]))+c3); 36 if (j!=m) 37 f[now][j+1][2]=min(min(f[now][j+1][2],f[now][j][2]),min(min(f[now][j][1],f[now][j][0]),f[now][j][3])+c2); 38 if (j!=m&&a1[j+1]==a2[i+1]) 39 { 40 f[nxt][j+1][0]=min(min(f[nxt][j+1][0],f[now][j][0]),min(min(f[now][j][1],f[now][j][2]),f[now][j][3])+c1); 41 } 42 if (j!=m&&((a2[i+1]^1)==a1[j+1])) 43 { 44 f[nxt][j+1][1]=min(min(f[nxt][j+1][1],f[now][j][1]),min(min(f[now][j][0],f[now][j][2]),f[now][j][3])+c1); 45 } 46 } 47 memset(f[now],127/3,sizeof(f[now])); 48 swap(now,nxt); 49 } 50 ans=inf; 51 for (i=0;i<=m;i++) 52 ans=min(ans,min(min(f[now][i][0],f[now][i][1]),min(f[now][i][2],f[now][i][3]))); 53 cout<<ans; 54 }

