乘法表
[Description]
Gemini 君送给 Kroulis 君一个活动的乘法表,它的结构是这样的。 首先,是一张硬纸板,上
面有 9x18 的方格:

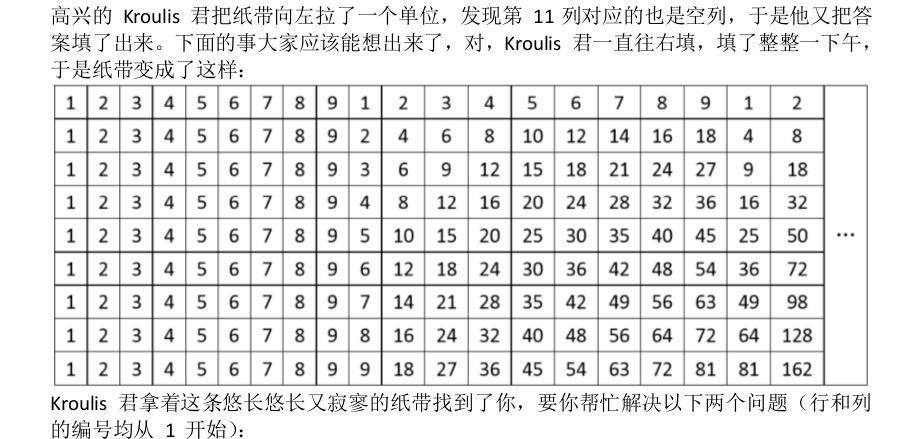
1. 第 i 行,第 j 列(坐标为(i,j))的数字是多少;
2. 从(i,j)到(m,n)这个子矩阵的和是多少。 当然,由于答案可能很大,所以请输出答案对
10007 取模的结果。 另外,由于 Kroulis 君的变态心理,所有数字(除了 x)均以三
进制方式给出(我也不知道 为什么)。
[Input]
第一行一个整数 x,表示询问的是哪个问题; 如果 x = 1,第二行两个三进制整数 i, j;
否则第二行四个三进制整数 i, j, m, n。
[Output]
一行一个十进制整数,为答案对 10007 取模后的结果。
[Sample]
[Tips]
各组数据范围如下:

归纳
以8为例,那一行我们可以写成
1×8^0,2*8^0,......9*8^0,1*8^1,.......,9*8^1,...........(x%9?x%9:9)*8^(x-1/9)
那么我们就可以通过归纳直接求出1询问
至于2询问,我们将上式变形:
(1+2+3+4+5+6+7+8+9)*(8^0+8^1+8^2+...8^(x/9-1))+(1+....+x%9)*8^(x/9)
但是读入的数很大,long long会爆
但是我们发现除以9可以用long long
所以用数组储存,每次记下两个值:x%9,x/9
x/9直接右移两位就行了
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 typedef long long lol; 8 char s[1001]; 9 lol Mod=10007,A[11],ans,pw[40],top; 10 lol get1(lol x) 11 { 12 lol p=1; 13 lol s=0; 14 while (x) 15 { 16 s+=p*(x%10); 17 x/=10; 18 p*=3; 19 } 20 return s; 21 } 22 void reduce(char *c) 23 {int i; 24 top=strlen(c); 25 c[top-1]--; 26 for (i=top-1;i>=0;i--) 27 if (c[i]<'0') 28 { 29 c[i]+=3,c[i-1]-=1; 30 } 31 } 32 void get2(char* x,lol &a,lol &b) 33 {int i; 34 top=strlen(x); 35 for (i=0;i<top;i++) 36 a=(a*3+x[i]-'0')%9; 37 b=0; 38 for (i=0;i<top-2;i++) 39 b=b*3+x[i]-'0'; 40 } 41 lol qpow(lol x,lol y) 42 { 43 lol res=1; 44 while (y) 45 { 46 if (y&1) res=res*x%Mod; 47 x=x*x%Mod; 48 y=y/2; 49 } 50 return res; 51 } 52 lol count(lol x,lol p1,lol p2) 53 {lol i; 54 if (p1==0&&p2==0) return 0; 55 if (x==1) 56 { 57 lol s=0; 58 if (p2-1>=0) 59 s=45*(p2)%Mod; 60 lol cnt=0; 61 for (i=1;i<=p1;i++) 62 cnt+=i; 63 s=(s+cnt)%Mod; 64 return s; 65 } 66 lol s=0; 67 if (p2-1>=0) 68 s=45*((qpow(x,(p2)%10006)-1+Mod)%Mod)*A[x-1]%Mod; 69 lol cnt=0; 70 for (i=1;i<=p1;i++) 71 cnt+=i; 72 s=(s+cnt*qpow(x,(p2)%10006)%Mod)%Mod; 73 return s; 74 } 75 int main() 76 {int opt,i; 77 lol d1,d2,t1,t2,x,y,n,m; 78 freopen("multi.in","r",stdin); 79 freopen("multi.out","w",stdout); 80 cin>>opt; 81 pw[0]=1; 82 for (i=1;i<=39;i++) 83 pw[i]=pw[i-1]*3; 84 if (opt==1) 85 { 86 scanf("%lld",&x); 87 cin>>s; 88 x=get1(x); 89 get2(s,d1,d2); 90 lol zyys=d1;lol mi=d2; 91 if (zyys==0) zyys=9,mi-=1; 92 ans=(zyys)*qpow(x,mi%10006)%Mod; 93 printf("%lld\n",ans); 94 } 95 else 96 { 97 scanf("%lld",&x); 98 scanf("%s",s); 99 x=get1(x); 100 reduce(s); 101 get2(s,d1,d2); 102 scanf("%lld",&n); 103 scanf("%s",s); 104 n=get1(n); 105 get2(s,t1,t2); 106 A[1]=1;A[0]=1; 107 for (i=2;i<=9;i++) 108 A[i]=(Mod-Mod/i)*A[Mod%i]%Mod; 109 for (i=x;i<=n;i++) 110 { 111 ans+=(count(i,t1,t2)-count(i,d1,d2)+Mod)%Mod; 112 ans%=Mod; 113 } 114 cout<<ans; 115 } 116 }

