[HAOI2011]Problem c

题目描述

给n个人安排座位，先给每个人一个1~n的编号，设第i个人的编号为ai（不同人的编号可以相同），接着从第一个人开始，大家依次入座，第i个人来 了以后尝试坐到ai，如果ai被占据了，就尝试ai+1，ai+1也被占据了的话就尝试ai+2，……，如果一直尝试到第n个都不行，该安排方案就不合 法。然而有m个人的编号已经确定(他们或许贿赂了你的上司...)，你只能安排剩下的人的编号，求有多少种合法的安排方案。由于答案可能很大，只需输出其 除以M后的余数即可。

输入输出格式

输入格式：

第一行一个整数T，表示数据组数

对于每组数据，第一行有三个整数，分别表示n、m、M

若m不为0，则接下来一行有m对整数，p1、q1，p2、q2 ,…, pm、qm，其中第i对整数pi、qi表示第pi个人的编号必须为qi

输出格式：

对于每组数据输出一行，若是有解则输出YES，后跟一个整数表示方案数mod M，注意，YES和数之间只有一个空格，否则输出NO

输入输出样例

输入样例#1：

2
4 3 10
1 2 2 1 3 1
10 3 8882
7 9 2 9 5 10

输出样例#1：

YES 4
NO

说明

100%的数据满足：1≤T≤10，1≤n≤300，0≤m≤n，2≤M≤109，1≤pi、qi≤n 且保证pi互不相同。

首先，每个人都要有位置

那么意味着位置不能有空

也就是说，对于位置i，位置在i及i前面的人要大于i个，否则就填不满

每个i都符合条件则为合法

我们设sum[i]为可以填在1～i的人数

cnt[i]为必须填i的人数

显然sum可以通过cnt算出，具体方法:

sum[0]=n-m,sum[i]=sum[i-1]+cnt[i]

原因sum[i]肯定有∑cnt[1~i]然后算上不确定的n-m个人

这样就可以用sum[i]<i判断无解

求方案数用dp

令f[i][j]表示前i位，放j个人

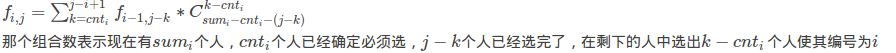
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
ll f[301][301],cnt[301],sum[301],C[301][301],Mod,n,m;
int main()
{int T,i,j,p,q,flag,k;
  cin>>T;
  while (T--)
    {
      cin>>n>>m>>Mod;
      memset(C,0,sizeof(C));
      memset(cnt,0,sizeof(cnt));
      memset(f,0,sizeof(f));
      C[0][0]=1;
      for (i=1;i<=300;i++)
    {C[i][0]=1;
      for (j=1;j<=i;j++)
        C[i][j]=C[i-1][j]+C[i-1][j-1],C[i][j]%=Mod;
    }
      for (i=1;i<=m;i++)
    {
      scanf("%d%d",&p,&q);
      cnt[q]++;
    }
      sum[0]=n-m;flag=1;
      for (i=1;i<=n;i++)
    {
      sum[i]=sum[i-1]+cnt[i];
      if (sum[i]<i) 
        {
          cout<<"NO\n";
          flag=0;break;
        }
    }
      if (flag) 
    {
      f[0][0]=1;
      for (i=1;i<=n;i++)
        {
          for (j=i;j<=sum[i];j++)
        {
          for (k=cnt[i];k<=j-i+1;k++)
            {
              f[i][j]+=f[i-1][j-k]*C[sum[i-1]-(j-k)][k-cnt[i]]%Mod;
              f[i][j]%=Mod;
            }
        }
        }
      cout<<"YES "<<f[n][n]<<endl;
    }
    }
}