计蒜客NOIP模拟赛4 D1T3 小X的佛光
小 X 是远近闻名的学佛,平日里最喜欢做的事就是蒸发学水。
小 X 所在的城市 X 城是一个含有 N 个节点的无向图,同时,由于 X 国是一个发展中国家,为了节约城市建设的经费,X 国首相在建造 X 城时只建造 N – 1 条边,使得城市的各个地点能够相互到达。
小 X 计划蒸发 Q 天的学水,每一天会有一名学水从 A 地走到 B 地,并在沿途各个地点留下一个水塘。此后,小 X 会从 C 地走到 B 地,并用佛光蒸发沿途的水塘。由于 X 城是一个学佛横行的城市,学水留下的水塘即使没有被小 X 蒸发,也会在第二天之前被其他学佛蒸发殆尽。
现在,小 X 想要知道,他每一天能够蒸发多少水塘呢?
输入格式
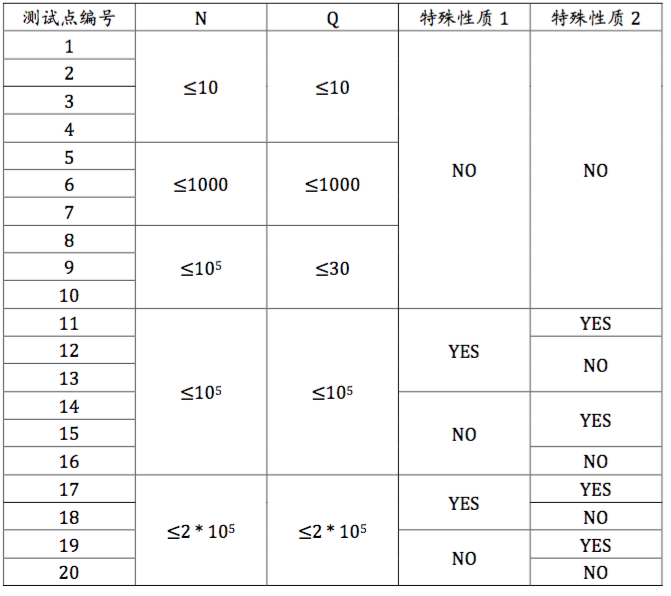
第一行三个整数 N,Q,num,分别表示 X 城地点的个数,小 X 蒸发学水的天数,以及测试点编号。注意,测试点编号是为了让选手们更方便的获得部分分,你可能不需要用到这则信息,在下发的样例中,测试点编号的含义是该样例满足某一测试点限制。
接下来 N – 1 行,每行两个整数 X,Y,表示 X 地与 Y 地之间有一条边。
接下来 Q 行,每行三个整数 A,B,C,表示一天中,有一名学水从 A 地走到 B 地,而小 X 会从 C 地走到 B 地。
输出格式
输出 Q 行,每行一个整数,表示小 X 能够蒸发的水塘数。
数据规模与约定
特殊性质 1:第 i 条边连接第 i 和第 i+1 个地点。
特殊性质 2:A=C。
样例输入
3 3 1 1 2 2 3 1 2 3 1 1 3 3 1 3
样例输出
1 1 3
A->B与B->C的共同路径长为
(LAB+LBC-LAC)/2
不过因为是点权,所以要+1
直接倍增LCA就行了
不过建树不能用dfs,会溢出,要用bfs()
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdio> 4 #include<cstring> 5 #include<queue> 6 using namespace std; 7 struct Node 8 { 9 int next,to; 10 }edge[400001]; 11 int num,head[200001]; 12 int n,q,dep[200001],fa[200001][20]; 13 bool vis[200001]; 14 void add(int u,int v) 15 { 16 num++; 17 edge[num].next=head[u]; 18 head[u]=num; 19 edge[num].to=v; 20 } 21 void bfs() 22 {int i; 23 queue<int>Q; 24 memset(vis,0,sizeof(vis)); 25 dep[1]=1; 26 Q.push(1); 27 vis[1]=1; 28 while (Q.empty()==0) 29 { 30 int u=Q.front(); 31 Q.pop(); 32 for (i=head[u];i;i=edge[i].next) 33 { 34 int v=edge[i].to; 35 if (vis[v]==0) 36 { 37 vis[v]=1; 38 dep[v]=dep[u]+1; 39 fa[v][0]=u; 40 Q.push(v); 41 } 42 } 43 } 44 } 45 int LCA(int x,int y) 46 {int i; 47 if (dep[x]<dep[y]) swap(x,y); 48 for (i=18;i>=0;i--) 49 if ((1<<i)<=dep[x]-dep[y]) x=fa[x][i]; 50 if (x==y) return x; 51 while (x!=y) 52 { 53 for (i=18;i>=0;i--) 54 if (fa[x][i]!=fa[y][i]) 55 { 56 x=fa[x][i]; 57 y=fa[y][i]; 58 } 59 60 if (x==y) return x; 61 x=fa[x][0]; 62 y=fa[y][0]; 63 } 64 return x; 65 } 66 int main() 67 {int x,y,i,a,b,c,j; 68 cin>>n>>q>>x; 69 for (i=1;i<=n-1;i++) 70 { 71 scanf("%d%d",&x,&y); 72 add(x,y);add(y,x); 73 } 74 bfs(); 75 for (i=1;i<=n;i++) 76 { 77 for (j=1;j<=18;j++) 78 fa[i][j]=fa[fa[i][j-1]][j-1]; 79 } 80 for (i=1;i<=q;i++) 81 { 82 scanf("%d%d%d",&a,&b,&c); 83 int l1=LCA(a,b),l2=LCA(b,c),l3=LCA(a,c); 84 int s1=dep[a]-dep[l1]+dep[b]-dep[l1]; 85 int s2=dep[b]-dep[l2]+dep[c]-dep[l2]; 86 int s3=dep[a]-dep[l3]+dep[c]-dep[l3]; 87 printf("%d\n",(s1+s2-s3)/2+1); 88 } 89 }