计蒜客NOIP模拟赛4 D1T2小X的密室

小 X 正困在一个密室里，他希望尽快逃出密室。

密室中有 N 个房间，初始时，小 X 在 1 号房间，而出口在 N 号房间。

密室的每一个房间中可能有着一些钥匙和一些传送门，一个传送门会单向地创造一条从房间 X 到房间 Y 的通道。另外，想要通过某个传送门，就必须具备一些种类的钥匙（每种钥匙都要有才能通过）。幸运的是，钥匙在打开传送门的封印后，并不会消失。

然而，通过密室的传送门需要耗费大量的时间，因此，小 X 希望通过尽可能少的传送门到达出口，你能告诉小 X 这个数值吗？

另外，小 X 有可能不能逃出这个密室，如果是这样，请输出 "No Solution"。

输入格式

第一行三个整数 N,M,K，分别表示房间的数量、传送门的数量以及钥匙的种类数。

接下来 N 行，每行 K 个 0 或 1，若第 i 个数为 1，则表示该房间内有第 i种钥匙，若第 i 个数为 0，则表示该房间内没有第 i种钥匙。

接下来 M 行，每行先读入两个整数 X,Y，表示该传送门是建立在 X号房间，通向 Y 号房间的，再读入 K 个 0 或 1，若第 i 个数为 1，则表示通过该传送门需要 i 种钥匙，若第 i 个数为 0，则表示通过该传送门不需要第 iii 种钥匙。

输出格式

输出一行一个 "No Solution"，或一个整数，表示最少通过的传送门数。

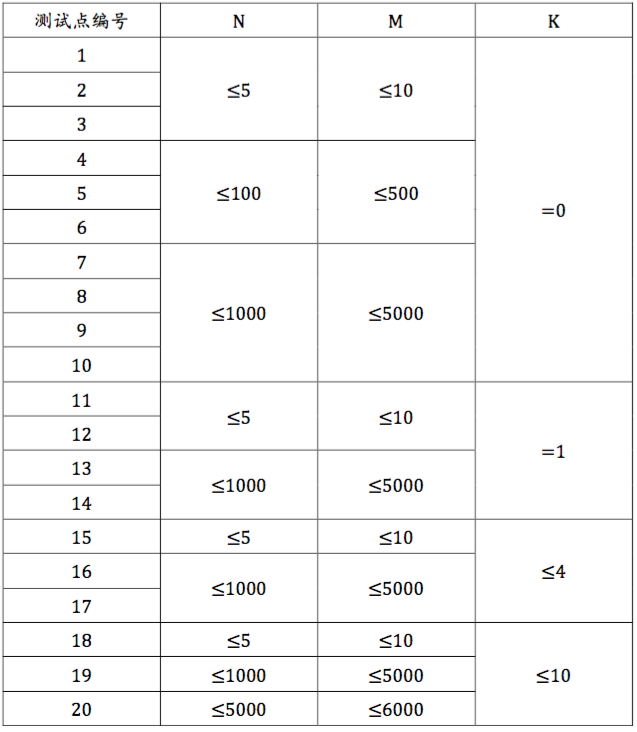
数据规模与约定

样例输入1

3 3 2
1 0
0 1
0 0
1 3 1 1
1 2 1 0
2 3 1 1

样例输出1

2

样例输入2

20 40 0
10 18 
18 14 
19 13 
4 14 
13 10 
5 18 
14 1 
13 13 
10 16 
19 11 
11 15 
10 18 
5 8 
12 19 
7 8 
18 6 
14 5 
9 5 
2 17 
13 14 
18 15 
8 18 
7 1 
13 5 
4 6 
17 4 
1 4 
10 10 
13 8 
19 2 
4 9 
3 3 
5 10 
17 5 
12 8 
19 11 
3 16 
17 10 
18 16 
13 13

样例输出2

No Solution

样例输入3

20 50 0
8 10 
7 17 
5 11 
14 20 
20 16 
8 19 
12 11 
18 7 
17 5 
4 15 
16 11 
11 8 
10 12 
8 9 
16 8 
3 16 
1 6 
3 20 
6 10 
11 12 
6 8 
18 17 
14 17 
3 11 
4 19 
9 2 
8 6 
13 2 
5 2 
12 19 
8 10 
14 7 
6 12 
6 4 
13 2 
8 7 
13 19 
17 9 
3 14 
18 20 
2 14 
4 17 
20 15 
14 15 
2 15 
7 20 
12 12 
18 10 
15 9 
15 9

样例输出3

4

裸的搜索
把钥匙的状态压缩为二进制数x<1024
判断能否传送？
边权为需要钥匙的状态
dis&x==dis那么就可以传送
 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<queue>
 6 using namespace std;
 7 struct Node
 8 {
 9     int next,to,dis;
10 }edge[50001];
11 struct zt
12 {
13     int x,t;
14 };
15 int num,head[5001];
16 int dist[5001][1501],key[5001],n,k,m;
17 bool vis[5001][1501];
18 void add(int u,int v,int dis)
19 {
20     num++;
21     edge[num].next=head[u];
22     head[u]=num;
23     edge[num].to=v;
24     edge[num].dis=dis;
25 }
26 void SPFA()
27 {int i;
28     queue<zt> Q;
29     memset(dist,127/3,sizeof(dist));
30     Q.push((zt){1,key[1]});
31     dist[1][key[1]]=0;
32    while (Q.empty()==0)
33     {
34        zt u=Q.front();
35        Q.pop();
36        vis[u.x][u.t]=0;
37          for (i=head[u.x];i;i=edge[i].next)
38          {
39              int v=edge[i].to;
40              if ((edge[i].dis&u.t)==edge[i].dis&&dist[v][u.t|key[v]]>dist[u.x][u.t]+1)
41              {
42                  dist[v][u.t|key[v]]=dist[u.x][u.t]+1;
43                  if (v==n)
44                  {
45                      cout<<dist[v][u.t|key[v]];
46                      return;
47                  }
48                  if (vis[v][u.t|key[v]]==0)
49                  {
50                      vis[v][u.t|key[v]]=1;
51                      Q.push((zt){v,u.t|key[v]});
52                  }
53              }
54          }
55     }
56     cout<<"No Solution";
57     return;
58 }
59 int main()
60 {int i,j,x,l,r;
61     cin>>n>>m>>k;
62     for (i=1;i<=n;i++)
63     {
64         for (j=1;j<=k;j++)
65         {scanf("%d",&x);
66             if (x) key[i]|=(1<<j-1);
67         }
68     }
69     for (i=1;i<=m;i++)
70     {
71         scanf("%d%d",&l,&r);
72         int dis=0;
73         for (j=1;j<=k;j++)
74         {scanf("%d",&x);
75             if (x) dis|=(1<<j-1);
76         }
77         add(l,r,dis);
78     }    
79     SPFA();
80 }

 

posted @ 2017-09-24 19:37  Z-Y-Y-S  阅读(713)  评论(1)  编辑  收藏  举报