计蒜客NOIP模拟赛D2T2 直线的交点
伦伦刚刚在高中学习了解析几何，学会了计算两条直线的交点。这天，老师给她布置了一道作业。在平面上有 nnn 条直线，他们之间有若干交点。给定一对平板（两条平行的直线），问这有多少对直线，他们的交点在这一对平板之间（注意 (i, j) 和 (j, i) 只算一对）。
输入格式
第一行三个整数 k,a,b 表示平板的两条平行直线的方程为 y=kx+a 和 y=kx+b，保证 a<b。
第二行一个整数 n。
接下来 n行每行两个整数 ki,bii,bi 表示第 iii 条直线的方程 y=kix+biy=k_ix+b_iy=kix+bi。
输出格式
一个整数，表示有多少对直线，他们的交点在平板之间。
数据范围与约定
对于 30%的数据，n≤5000。
对于 100%的数据，n≤100000。
为了简单起见，输入数据保证，没有直线和平板平行，没有两条直线的交点在平板上。
样例解释
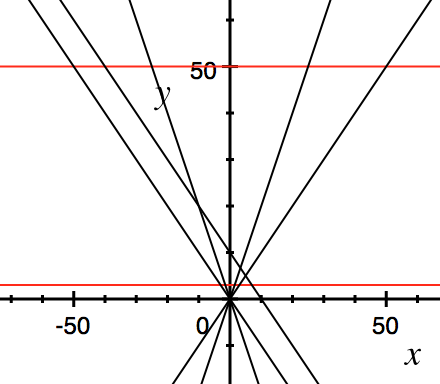
只有 y=−x+10这条直线和 y=x,y=2x,y=−2x 这三条直线的交点在区域内。
样例输入
0 3 50 5 1 0 2 0 -1 0 -2 0 -1 10
样例输出
3
我们要用到以下观察，若两条直线的交点在平板内部。
则他们与下方平板和上方平板的交点横坐标大小关系相反。
这表明，如果将所有直线按照他们与下方平板的交点的横坐标排序，
将他们上方平板交点的横坐标作为关键字。
则平板内交点个数等于在排序后的序列中关于关键字的逆序对个数。
于是用归并排序来计算逆序对个数即可
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 struct Line 7 { 8 double x1,x2; 9 }line[100001],t[100001]; 10 int n; 11 double k1,a1,b1; 12 double k,b; 13 long long ans; 14 bool cmp(Line a,Line b) 15 { 16 return a.x1<b.x1; 17 } 18 void partition(int l,int r) 19 { 20 if (l>=r) 21 return; 22 int mid=(l+r)/2; 23 partition(l,mid); 24 partition(mid+1,r); 25 int i=l,j=mid+1,k=l; 26 while(i<=mid&&j<=r) 27 { 28 if(line[i].x2>line[j].x2) 29 { 30 ans=(ans+mid-i+1); 31 t[k]=line[j]; 32 k++; 33 j++; 34 } 35 else 36 { 37 t[k]=line[i]; 38 k++; 39 i++; 40 } 41 } 42 while(i<=mid) 43 { 44 t[k]=line[i]; 45 k++; 46 i++; 47 } 48 while(j<=r) 49 { 50 t[k]=line[j]; 51 k++; 52 j++; 53 } 54 for(i=l; i<=r; i++) 55 line[i]=t[i]; 56 } 57 int main() 58 {int i; 59 cin>>k1>>a1>>b1; 60 cin>>n; 61 for (i=1;i<=n;i++) 62 { 63 scanf("%lf%lf",&k,&b); 64 line[i].x1=(b1-b)/(k-k1); 65 line[i].x2=(a1-b)/(k-k1); 66 } 67 sort(line+1,line+n+1,cmp); 68 partition(1,n); 69 cout<<ans; 70 }
