NOIP 2008 双栈排序
题目描述
Tom最近在研究一个有趣的排序问题。如图所示,通过2个栈S1和S2,Tom希望借助以下4种操作实现将输入序列升序排序。
操作a
如果输入序列不为空,将第一个元素压入栈S1
操作b
如果栈S1不为空,将S1栈顶元素弹出至输出序列
操作c
如果输入序列不为空,将第一个元素压入栈S2
操作d
如果栈S2不为空,将S2栈顶元素弹出至输出序列
如果一个1~n的排列P可以通过一系列操作使得输出序列为1,2,…,(n-1),n,Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”,而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列:<a,c,c,b,a,d,d,b>
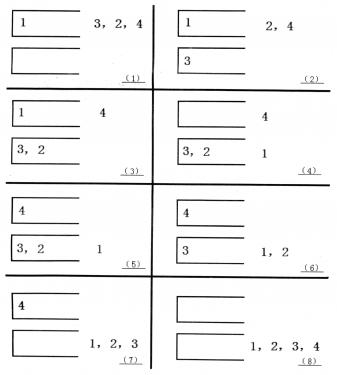
当然,这样的操作序列有可能有几个,对于上例(1,3,2,4),<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。
输入输出格式
输入格式:输入文件twostack.in的第一行是一个整数n。
第二行有n个用空格隔开的正整数,构成一个1~n的排列。
输出格式:输出文件twostack.out共一行,如果输入的排列不是“可双栈排序排列”,输出数字0;否则输出字典序最小的操作序列,每两个操作之间用空格隔开,行尾没有空格。
输入输出样例
【输入样例1】 4 1 3 2 4 【输入样例2】 4 2 3 4 1 【输入样例3】 3 2 3 1
【输出样例1】 a b a a b b a b 【输出样例2】 0 【输出样例3】 a c a b b d
说明
30%的数据满足: n<=10
50%的数据满足: n<=50
100%的数据满足: n<=1000
首先考虑一个简单情况——单栈排序,显然有这样的一个事实:
a[i]和a[j] 不能压入同一个栈⇔存在一个k,使得i<j<k且a[k]<a[i]<a[j]
时间复杂度为O(n^3).对于n<=1000仍显吃力,对此可以用动态规划的思想,将上述复杂度降到O(n^2)。
状态:f[i]=min(a[i],a[i+1], ... ,a[n])
边界条件:f[n+1]=INF;
状态转移方程:f[i]=min(f[i+1],a[i]);
于是上述判断就转化为了f[j+1]<a[i] && a[i]<a[j]
如果a[i]和a[j]不能在一个栈内,即连接一条i与j之间的无向边,接下来我们只需要判断这个图是否为二分图
由于题目中说编号的字典序要尽可能的小,那么就把编号小的尽可能放到stack1
判断二分图的方法可以采用黑白染色的方式,先从编号小的开始染,第一个顶点染成黑色,相邻的顶点染成不同的颜色,如果发现黑白冲突,那么说明这个图不是一个二分图,是不合法的,输出0.
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<stack> 6 using namespace std; 7 struct Node 8 { 9 int next,to; 10 }edge[400001]; 11 int num,head[2001],f[2002],cnt; 12 int vis[2002],n,a[2002]; 13 stack<int>s1,s2; 14 void add(int u,int v) 15 { 16 num++; 17 edge[num].next=head[u]; 18 head[u]=num; 19 edge[num].to=v; 20 } 21 bool dfs(int x) 22 {int i; 23 for (i=head[x];i;i=edge[i].next) 24 { 25 int v=edge[i].to; 26 if (vis[v]==0) 27 { 28 if (vis[x]==1) 29 vis[v]=2; 30 else vis[v]=1; 31 if (!dfs(v)) return 0; 32 } 33 else 34 if (vis[x]==vis[v]) return 0; 35 } 36 return 1; 37 } 38 int main() 39 {int i,j; 40 cin>>n; 41 for (i=1;i<=n;i++) 42 scanf("%d",&a[i]); 43 f[n+1]=2e9; 44 for (i=n;i>=1;i--) 45 f[i]=min(f[i+1],a[i]); 46 for (i=1;i<=n;i++) 47 { 48 for (j=i+1;j<=n;j++) 49 { 50 if (f[j+1]<a[i]&&a[i]<a[j]) 51 { 52 add(i,j); 53 add(j,i); 54 } 55 } 56 } 57 for (i=1;i<=n;i++) 58 if (vis[i]==0) 59 { 60 vis[i]=1; 61 if (!dfs(i)) 62 { 63 cout<<0<<endl; 64 return 0; 65 } 66 } 67 cnt=1; 68 for (i=1;i<=n;i++) 69 { 70 if (vis[i]==1) 71 { 72 s1.push(a[i]); 73 printf("a "); 74 } 75 else if (vis[i]==2) 76 { 77 s2.push(a[i]); 78 printf("c "); 79 } 80 81 while ((!s1.empty()&&s1.top()==cnt)||(!s2.empty()&&s2.top()==cnt)) 82 { 83 if (s1.top()==cnt) 84 { 85 printf("b "); 86 s1.pop(); 87 } 88 else 89 { 90 printf("d "); 91 s2.pop(); 92 } 93 cnt++; 94 } 95 } 96 }

