[SCOI2010]生成字符串
题目描述
lxhgww最近接到了一个生成字符串的任务,任务需要他把n个1和m个0组成字符串,但是任务还要求在组成的字符串中,在任意的前k个字符中,1的个数不能少于0的个数。现在lxhgww想要知道满足要求的字符串共有多少个,聪明的程序员们,你们能帮助他吗?
输入输出格式
输入格式:
输入数据是一行,包括2个数字n和m
输出格式:
输出数据是一行,包括1个数字,表示满足要求的字符串数目,这个数可能会很大,只需输出这个数除以20100403的余数
输入输出样例
输入样例#1:
2 2
输出样例#1:
2
说明
limitation
每点2秒
对于30%的数据,保证1<=m<=n<=1000
对于100%的数据,保证1<=m<=n<=1000000
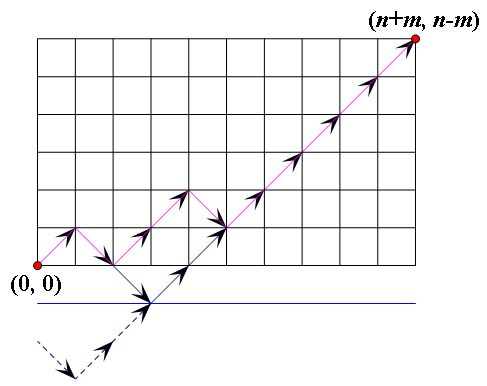
首先,我们设选1为(1,1),选0为(1,-1)
目标就是(n+m,n-m)
总方案数为C(n+m,n),因为有n+m个位置,放n个1
然后要减去不合法的即线路通过y=-1的。将线路与y=-1交点的左边沿着y=-1做对称操作,则最后等价于从(0,-2)走到(n+m,n-m)的方案数
所以向上走n-m+2
则有x-y=n-m+2
x+y=n+m
x=n+1,y=m-1
所以不合法方案为C(n+m,n+1)
ans=C(n+m,n)-C(n+m,n+1)
求这些用模逆元,O(n)求解
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 long long A[2000001],B[2000001],ans1,ans2; 7 int n,m,Mod=20100403; 8 int main() 9 {int i,j; 10 cin>>n>>m; 11 A[1]=1; 12 for (i=2;i<=n+m;i++) 13 A[i]=((Mod-Mod/i)*A[Mod%i])%Mod; 14 for (i=2;i<=n+m;i++) 15 A[i]=(A[i]*A[i-1])%Mod; 16 B[0]=1; 17 for (i=1;i<=n+m;i++) 18 B[i]=(B[i-1]*i)%Mod; 19 ans1=(((B[n+m]*A[n])%Mod)*A[m])%Mod; 20 ans2=(((B[n+m]*A[n+1])%Mod)*A[m-1])%Mod; 21 cout<<(ans1-ans2+Mod)%Mod; 22 }




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通