POJ 2826 An Easy Problem?!
题意:
给出平面上的两条线段,现在有竖直下落的雨;
求这两条线段最多能接到多少雨;
Input
The first line contains the number of test cases.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x1, y1, x2, y2, x3, y3, x4, y4. (x1, y1), (x2, y2) are the endpoints of one board, and (x3, y3), (x4, y4) are the endpoints of the other one.
Each test case consists of 8 integers not exceeding 10,000 by absolute value, x1, y1, x2, y2, x3, y3, x4, y4. (x1, y1), (x2, y2) are the endpoints of one board, and (x3, y3), (x4, y4) are the endpoints of the other one.
Output
For each test case output a single line containing a real number with precision up to two decimal places - the amount of rain collected.
Sample Input
2
0 1 1 0
1 0 2 1
0 1 2 1
1 0 1 2
Sample Output
1.00
0.00
题解:
无水时有三种情况
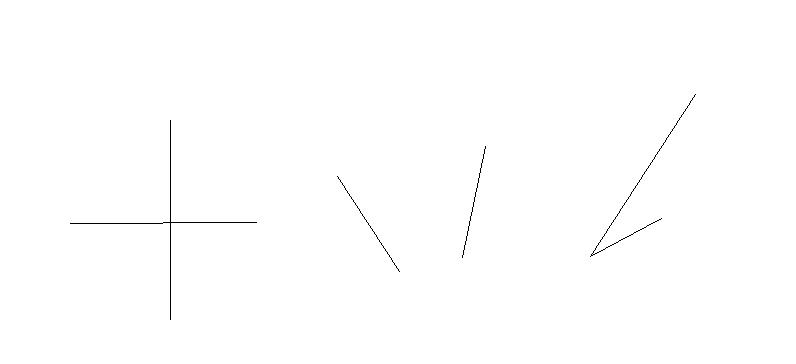
尤其是第三种情况,很难想到
第一种:有直线平行x轴,直接判断
第二种:不相交,叉积判断即可
第三种:下面再详细说明
会发现这个类似木桶效应,水存多少是取决于最低的y的,这样如果我们找到决定水平面的那个y
再通过y解出tx1和tx2,来判断线段的左右关系,再通过左右关系特判
如果以上情况都没有,则求面积
解出交点jx,jy,求(tx1,y)-(jx,jy),(tx2,y)-(jx,jy)的叉积绝对值再除2
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 double eps=1e-8; 8 int dcmp(double x) 9 { 10 if (abs(x)<=eps) return 0; 11 if (x>0) return 1; 12 else return -1; 13 } 14 double count_k(double x2,double x1,double y2,double y1) 15 { 16 return ((y2-y1)/(x2-x1)); 17 } 18 double det(double x1,double y1,double x2,double y2) 19 { 20 return x1*y2-x2*y1; 21 } 22 int main() 23 {int T; 24 double x1,y1,x2,y2,x3,y3,x4,y4,ty,tx1,tx2,jy,jx; 25 cin>>T; 26 while (T--) 27 { 28 scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&y1,&x2,&y2,&x3,&y3,&x4,&y4); 29 if (y3<y4) swap(y3,y4),swap(x3,x4); 30 if (y1<y2) swap(y1,y2),swap(x1,x2); 31 if (dcmp(y1-y2)==0||dcmp(y3-y4)==0) 32 { 33 printf("0.00\n"); 34 } 35 else if (dcmp(count_k(x2,x1,y2,y1)-count_k(x4,x3,y4,y3))==0) 36 { 37 printf("0.00\n"); 38 } 39 else 40 { 41 double k1=det(x2-x1,y2-y1,x3-x1,y3-y1); 42 double k2=det(x2-x1,y2-y1,x4-x1,y4-y1); 43 double k3=det(x4-x3,y4-y3,x2-x3,y2-y3); 44 double k4=det(x4-x3,y4-y3,x1-x3,y1-y3); 45 if (dcmp(k1*k2)<=0&&dcmp(k3*k4)<=0)//相交 46 { 47 ty=min(max(y1,y2),max(y3,y4)); 48 tx1=(x2*(ty-y1)-x1*(ty-y2))/(y2-y1); 49 tx2=(x4*(ty-y3)-x3*(ty-y4))/(y4-y3); 50 //cout<<tx1<<' '<<tx2<<endl; 51 if (dcmp(tx1-tx2)==-1&&dcmp(x1-x3)!=-1)//直线1在左边,且x1>=x3 52 { 53 printf("0.00\n"); 54 } 55 else if (dcmp(tx1-tx2)==1&&dcmp(x3-x1)!=-1)//直线在右边,且x1<=x3 56 {//cout<<'a'; 57 printf("0.00\n"); 58 } 59 else 60 { 61 jx=((x4*y3-x3*y4)*(x2-x1)-(x2*y1-x1*y2)*(x4-x3))/((y2-y1)*(x4-x3)-(y4-y3)*(x2-x1)); 62 jy=(jx*(y2-y1)+x2*y1-x1*y2)/(x2-x1);//解出交点 63 double s=abs(det(tx2-jx,ty-jy,tx1-jx,ty-jy))/2;//求面积 64 printf("%.2lf\n",s); 65 } 66 } 67 else 68 { 69 printf("0.00\n"); 70 } 71 } 72 } 73 }


