POJ 3347 Kadj Squares
题目大意:
给定一个数 n ,表示有 n 个正方形,然后n个整数,表示正方形的的边长,将正方形旋转45°,
每个正方形都尽量靠左摆放,问的是从上往下看,能够看到几个正方形。
输入:
一个数字T,表示数据组数
每一组数据,n表示正方形数量,接下来n(n<=30)个数,表示边长
输出:
可以看到的矩形
Sample Input
4
3 5 1 4
3
2 1 2
0
Sample Output
1 2 4 1 3
题解:
对于一个矩形,已知前面的矩形,可以O(n)求出左的坐标,
注意此处不能只与前一个矩形比较求左坐标,必须要与所有矩形求一次左坐标,再去最大值
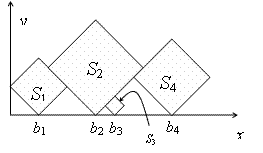
就拿题目的图举例:
黑色加粗的矩形是只与前一个矩形比较求出的,显然不符合,因为没有考虑其他矩形的约束
求出n个矩形的坐标后,要判断投影的覆盖情况
对于一个点i,前j=1~i-1个点如果满足r[j]>l[i]&&len[j]>len[i]则说明对于i来说l[i]~r[j]这一段已无法看见,直接
l[i]=r[j]
同理后j=i+1~n个点满足l[j]<r[i]&&len[j]>len[i]则说明对于i来说l[j]~r[i]这一段已无法看见,直接r[i]=l[j]
判断i是否被覆盖只要判断l[i]<r[i]就行了
本题还有一个保证精度的技巧:因为我们发现,会出现精度问题是因为每次求坐标都涉及乘√2
将所有坐标扩大√2倍即可
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 using namespace std; 7 struct Node 8 { 9 double left,right; 10 }node[100001]; 11 int n; 12 double len[10001]; 13 int main() 14 {int i,j; 15 while (cin>>n&&n) 16 { 17 scanf("%lf",&len[1]); 18 memset(node,0,sizeof(node)); 19 node[1].left=0; 20 node[1].right=2*len[1]; 21 for (i=2;i<=n;i++) 22 { 23 scanf("%lf",&len[i]); 24 for (j=1;j<i;j++) 25 node[i].left=max(node[i].left,node[j].right-abs(len[i]-len[j])); 26 node[i].right=node[i].left+2*len[i]; 27 } 28 for (i=1;i<=n;i++) 29 { 30 for (j=1;j<i;j++) 31 { 32 if (node[j].right>node[i].left&&len[j]>len[i]) node[i].left=node[j].right; 33 } 34 for (j=i+1;j<=n;j++) 35 { 36 if (node[j].left<node[i].right&&len[j]>len[i]) node[i].right=node[j].left; 37 } 38 } 39 // for (i=1;i<=n;i++) 40 // cout<<node[i].left<<' '<<node[i].right<<endl; 41 bool first=1; 42 for (i=1;i<=n;i++) 43 if (node[i].left<node[i].right) 44 { 45 if (first) first=0; 46 else printf(" "); 47 printf("%d",i); 48 } 49 cout<<endl; 50 } 51 }