POJ 1066 Treasure Hunt

题目大意：

一个正方形的墓葬内有n堵墙，每堵墙的两个顶点都在正方形的边界上，现在这些墙将墓葬分割成了很多小空间，

已知正方形内的一个点上存在宝藏，现在我们要在正方形的外面去得到宝藏，对于每个小空间，我们可以炸开它的任意一条边的中点，

现在给出每堵墙的两个节点的坐标和宝藏的坐标，问如果要得到宝藏，需要炸的墙数最少是多少。

 

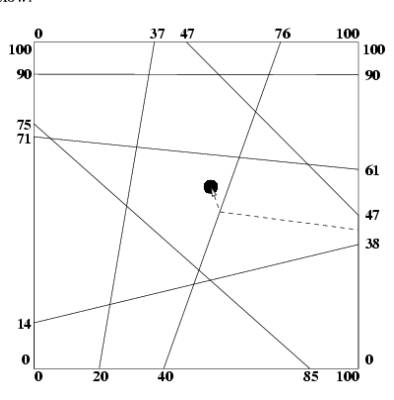
输入：

输入将包括一个案例。第一行是一个整数N（0≤N≤30）指定内墙的数量，其次是N行包含每个墙x1 y1 x2 y2整数点

内墙总是从一个外墙延伸到另一个外墙，并且布置成在任何点都不超过两个墙相交。你可以假设没有两个给定的墙重合。

输出
用下面所示的格式打印一行，列出需要创建的最小门数。

 

Sample Input

 

7 
20 0 37 100 
40 0 76 100 
85 0 0 75 
100 90 0 90 
0 71 100 61 
0 14 100 38 
100 47 47 100 
54.5 55.4 

 

Sample Output

Number of doors = 2

题解:

枚举正方形边界上的点作为进入正方形的节点，由这个点向宝藏连出一条线段，这条线段和多少个墙相交，那么就需要炸坏多少个墙，找出一个最小的值。

原因:因为每堵墙的两个节点都在边界上，所以如果和墙相交，那么就一定要跨过这道墙，所以需要炸掉它。

一定要是规范相交，因为如果枚举的点如果是一堵墙的节点，那么这堵墙是不应该被计算的。

事实上从一个点到终点不可能“绕过”围墙，只能穿过去，所以门是否开在中点是无所谓的，只要求四周线段中点到终点的线段与墙的最少交点个数即可。实际上，只需判断四周围墙的所有点与终点的连线与内墙的最少交点加一

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
using namespace std;
double x1[1001],y11[1001],x2[1001],y2[1001],sx,sy;
int n,ans;
bool exam(double x3,double y3,int i)
{
    double dx=x3-x1[i],dy=y3-y11[i];
    double px=x2[i]-x1[i],py=y2[i]-y11[i];
    double fx=sx-x1[i],fy=sy-y11[i];
    if ((dx*py-dy*px)*(px*fy-py*fx)<=0) return 0;
    dx=x1[i]-x3;dy=y11[i]-y3;
    px=sx-x3;py=sy-y3;
    fx=x2[i]-x3;fy=y2[i]-y3;
    if ((dx*py-dy*px)*(px*fy-py*fx)<=0) return 0;
return 1;
}
void solve(double x,double y)
{int s=0,i;
    for (i=1;i<=n;i++)
    {
        if (exam(x,y,i)) s++;
    }
    ans=min(ans,s);
}
int main()
{int i;
    cin>>n;
    ans=n;
    for (i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf%lf",&x1[i],&y11[i],&x2[i],&y2[i]);
    }
    scanf("%lf%lf",&sx,&sy);
     for (i=0;i<=100;i++)
     {
          solve(0,i);
          solve(100,i);
          solve(i,0);
          solve(i,100);
     }
     ans++;
     cout<<"Number of doors = ";
     cout<<ans<<endl;
}