[JSOI2004]平衡点

题目描述

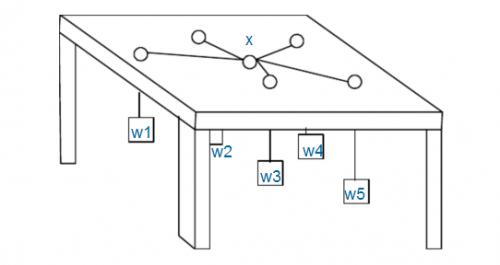
如图：有n个重物，每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞，然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的（不会造成能量损失），桌子足够高（因而重物不会垂到地上），且忽略所有的摩擦。

问绳结X最终平衡于何处。

注意：桌面上的洞都比绳结X小得多，所以即使某个重物特别重，绳结X也不可能穿过桌面上的洞掉下来，最多是卡在某个洞口处。

输入输出格式

输入格式：

文件的第一行为一个正整数n（1≤n≤1000），表示重物和洞的数目。接下来的n行，每行是3个整数：Xi.Yi.Wi，分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000 ） 

输出格式：

你的程序必须输出两个浮点数（保留小数点后三位），分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。

输入输出样例

输入样例#1：

3
0 0 1
0 2 1
1 1 1

输出样例#1：

0.577 1.000
题解：计算几何
首先定原点为平衡点，求出所有x，y方向上分力的和，求出合力，再移动平衡点
首先定下一个尺度k，每次平衡点移动以k为单位。如果尺度过大了，则缩小尺度，缩小量0.4~0.99随意
如果这时的合力大于这个尺度，我们就对这个已经设定好的平衡点进行调整，让它更加接近真实的平衡点。
当合力在尺度以内或者调整一定次数以后，我们减小尺度，再次进行调整。
这道题用到了一种调整思想，即不断逼近正解
ps：几个月后回来发现这其实是一道爬山算法(或模拟退火)题

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int n;
double x[1001],y[1001],w[1001],k,xa,ya,xx,yy,fx,fy,d;
int main()
{int i,j,p;
    cin>>n;
    for (i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf",&x[i],&y[i],&w[i]);
    }
    k=100;
    xa=0;ya=0;
     for (i=1;i<=100;i++)
     {
         xx=xa;yy=ya;
         for (p=1;p<=200;p++)
         {
             fx=0;fy=0;
             for (j=1;j<=n;j++)
             {
                 d=sqrt((xx-x[j])*(xx-x[j])+(yy-y[j])*(yy-y[j]));
                 if (d) 
                 {
                 double dx=x[j]-xx,dy=y[j]-yy;
                 fx+=dx/d*w[j];fy+=dy/d*w[j];
                 }
            }
            d=sqrt(fx*fx+fy*fy);
            if (d<=k) break;
            xx+=fx/d*k;yy+=fy/d*k;
        }
        xa=xx;ya=yy;
        k*=0.4;
     }
    printf("%.3lf %.3lf\n",xa,ya);
}