Picture
墙上贴着许多形状相同的海报、照片。它们的边都是水平和垂直的。每个矩形图片可能部分或全部的覆盖了其他图片。所有矩形合并后的边长称为周长。
题目描述
编写一个程序计算周长。
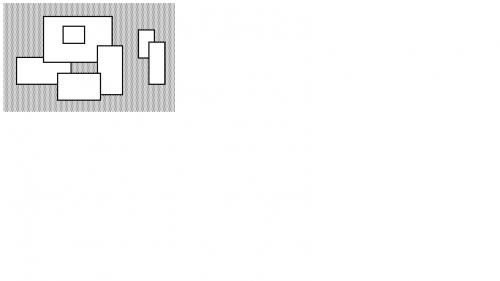
如图1所示7个矩形。
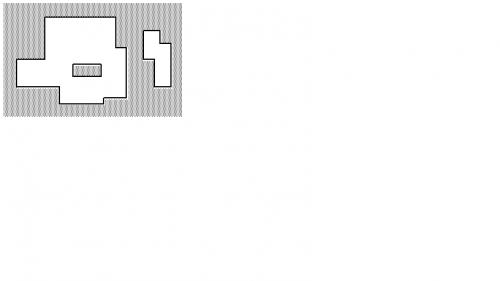
如图2所示,所有矩形的边界。所有矩形顶点的坐标都是整数。
输入输出格式
输入格式:
输入文件的第一行是一个整数N(0<=N<5000),表示有多少个矩形。接下来N行给出了每一个矩形左下角坐标和右上角坐标(所有坐标的数值范围都在-10000到10000之间)。
输出格式:
输出文件只有一个正整数,表示所有矩形的周长。
输入输出样例
输入样例#1:
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
输出样例#1:
228
题解:线段树扫描线
与altanis那题很像,其实每次扫描只要多算竖边的数量就行了。
由于没有发altantis的题解,在此解释一下扫描线(用altantis的角度)



扫描之前还需要做一个工作,就是保存好所有矩形的上下边,并且按照它们所处的高度进行排序,另外如果是上边我们给他一个值-1,下边给他一个值1,我们用一个结构体来保存所有的上下边 。
接着扫描线从下往上扫描,每遇到一条上下边就停下来,将这条线段投影到总区间上(总区间就是整个多边形横跨的长度),这个投影对应的其实是个插入和删除线段操作。
还记得给他们赋的值1或-1吗,下边是1,扫描到下边的话相当于往总区间插入一条线段,上边-1,扫描到上边相当于在总区间删除一条线段(如果说插入删除比较抽象,那么就直白说,扫描到下边,投影到总区间,对应的那一段的值都要增1,扫描到上边对应的那一段的值都要减1,如果总区间某一段的值为0,说明其实没有线段覆盖到它,为正数则有,那会不会为负数呢?是不可能的,可以自己思考一下)。
把思路转化到这道题上:
这道题也差不多,不过是加上竖边的长,但难点在可能会有多个竖边。
想一下,在线段树上,有多上个不为0的连续区间,就有2倍个竖边
动态维护这个竖边的数量,lseg表示区间最左边有无正数,rseg表示最右边
只要l[右子节点]&&r[左子节点]则两线相交,那么竖边数量-2
注意用位运算,可能会导致莫名其妙的内存超限
附图一张:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<set> 6 using namespace std; 7 struct Node 8 { 9 int lx,rx,y; 10 int s; 11 Node(){} 12 Node(int x1,int x2,int H,int c):lx(x1),rx(x2),y(H),s(c){} 13 bool operator <(const Node &S) const 14 { 15 return (y<S.y||(y==S.y&&s>S.s)); 16 } 17 }line[21001]; 18 int c[81001],segsum[82001],n,num,ans,sum[81001]; 19 bool lseg[81001],rseg[81001]; 20 void updata(int rt,int l,int r) 21 { 22 if (c[rt]) 23 { 24 segsum[rt]=2; 25 sum[rt]=r-l+1; 26 lseg[rt]=1; 27 rseg[rt]=1; 28 } 29 else 30 if (r==l) 31 { 32 lseg[rt]=0; 33 rseg[rt]=0; 34 segsum[rt]=0; 35 sum[rt]=0; 36 } 37 else 38 { 39 segsum[rt]=segsum[rt<<1]+segsum[rt<<1|1]; 40 sum[rt]=sum[rt<<1]+sum[rt<<1|1]; 41 if (lseg[rt<<1|1]&&rseg[rt<<1]) segsum[rt]-=2; 42 lseg[rt]=lseg[rt<<1]; 43 rseg[rt]=rseg[rt<<1|1]; 44 } 45 } 46 void update(int rt,int l,int r,int L,int R,int d) 47 { 48 if (l>=L&&r<=R) 49 { 50 c[rt]+=d; 51 updata(rt,l,r); 52 return; 53 } 54 int mid=(l+r)>>1; 55 //cout<<l<<' '<<r<<endl; 56 if (L<=mid) update(rt<<1,l,mid,L,R,d); 57 if (R>mid) update(rt<<1|1,mid+1,r,L,R,d); 58 updata(rt,l,r); 59 } 60 int main() 61 {int i,j,left=2e9,right=-2e9,last,x1,x2,y1,y2,l,r; 62 cin>>n; 63 for (i=1;i<=n;i++) 64 { 65 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 66 line[num++]=Node(x1,x2,y1,1); 67 line[num++]=Node(x1,x2,y2,-1); 68 left=min(left,x1); 69 right=max(right,x2); 70 } 71 sort(line,line+num); 72 last=0; 73 for (i=0;i<num;++i) 74 {//cout<<i<<endl; 75 l=line[i].lx; 76 r=line[i].rx-1; 77 if (l<=r) 78 update(1,left,right,l,r,line[i].s); 79 ans+=segsum[1]*(line[i+1].y-line[i].y); 80 ans+=abs(sum[1]-last); 81 last=sum[1]; 82 //cout<<ans<<endl; 83 } 84 cout<<ans; 85 }



