【Machine Learning】机器学习の特征

绘制了一张导图,有不对的地方欢迎指正:

下载地址

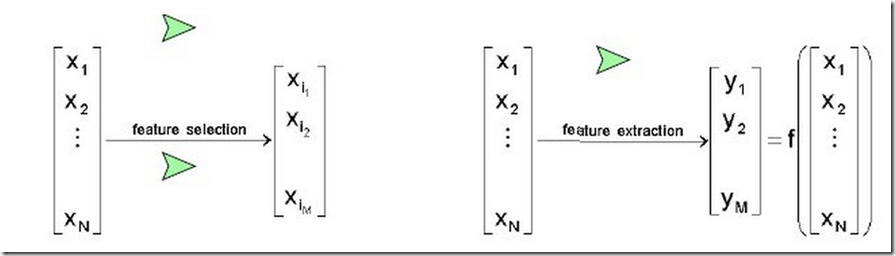
机器学习中,特征是很关键的.其中包括,特征的提取和特征的选择.他们是降维的两种方法,但又有所不同:

特征抽取（Feature Extraction）:Creatting a subset of new features by combinations of the exsiting features.也就是说，特征抽取后的新特征是原来特征的一个映射。

特征选择（Feature Selection）:choosing a subset of all the features(the ones more informative)。也就是说，特征选择后的特征是原来特征的一个子集。

特征提取

最好的情况下,当然是有专家知道该提取什么样的特征,但是在不知道的前提下,一般的降维方法可以派上用场:(from wiki)

（1）Signal representation(信号表示): The goal of the feature extraction mapping is to represent the samples accurately in a low-dimensional space. 也就是说，特征抽取后的特征要能够精确地表示样本信息，使得信息丢失很小。对应的方法是PCA.

（2）Signal classification（信号分类): The goal of the feature extraction mapping is toenhance the class-discriminatory information in a low-dimensional space. 也就是说，特征抽取后的特征，要使得分类后的准确率很高，不能比原来特征进行分类的准确率低。对与线性来说，对应的方法是LDA .

在图像处理方面,有广泛的应用.

特征选择

主要过程:

(1)产生过程

2.2.1完全搜索

　　完全搜索分为穷举搜索(Exhaustive)与非穷举搜索(Non-Exhaustive)两类。

　　(1) 广度优先搜索( Breadth First Search )

算法描述：广度优先遍历特征子空间。

　　算法评价：枚举了所有的特征组合，属于穷举搜索，时间复杂度是O(2ⁿ)，实用性不高。

　　(2)分支限界搜索( Branch and Bound )

算法描述：在穷举搜索的基础上加入分支限界。例如：若断定某些分支不可能搜索出比当前找到的最优解更优的解，则可以剪掉这些分支。

　　(3) 定向搜索 (Beam Search )

算法描述：首先选择N个得分最高的特征作为特征子集，将其加入一个限制最大长度的优先队列，每次从队列中取出得分最高的子集，然后穷举向该子集加入1个特征后产生的所有特征集，将这些特征集加入队列。

　　(4) 最优优先搜索 ( Best First Search )

算法描述：与定向搜索类似，唯一的不同点是不限制优先队列的长度。

2.2.2 启发式搜索

　　(1)序列前向选择( SFS , Sequential Forward Selection )

　　算法描述：特征子集X从空集开始，每次选择一个特征x加入特征子集X，使得特征函数J( X)最优。简单说就是，每次都选择一个使得评价函数的取值达到最优的特征加入，其实就是一种简单的贪心算法。

　　算法评价：缺点是只能加入特征而不能去除特征。例如：特征A完全依赖于特征B与C，可以认为如果加入了特征B与C则A就是多余的。假设序列前向选择算法首先将A加入特征集，然后又将B与C加入，那么特征子集中就包含了多余的特征A。

　　(2)序列后向选择( SBS , Sequential Backward Selection )

　　算法描述：从特征全集O开始，每次从特征集O中剔除一个特征x，使得剔除特征x后评价函数值达到最优。

　　算法评价：序列后向选择与序列前向选择正好相反，它的缺点是特征只能去除不能加入。

　　另外，SFS与SBS都属于贪心算法，容易陷入局部最优值。

　　(3) 双向搜索( BDS , Bidirectional Search )

　　算法描述：使用序列前向选择(SFS)从空集开始，同时使用序列后向选择(SBS)从全集开始搜索，当两者搜索到一个相同的特征子集C时停止搜索。

　　双向搜索的出发点是。如下图所示，O点代表搜索起点，A点代表搜索目标。灰色的圆代表单向搜索可能的搜索范围，绿色的2个圆表示某次双向搜索的搜索范围，容易证明绿色的面积必定要比灰色的要小。

图2. 双向搜索

　　(4) 增L去R选择算法 ( LRS , Plus-L Minus-R Selection )

　　该算法有两种形式:

　　　　　　<1> 算法从空集开始，每轮先加入L个特征，然后从中去除R个特征，使得评价函数值最优。( L > R )

　　　　<2> 算法从全集开始，每轮先去除R个特征，然后加入L个特征，使得评价函数值最优。( L < R )

　　算法评价：增L去R选择算法结合了序列前向选择与序列后向选择思想， L与R的选择是算法的关键。

　　(5) 序列浮动选择( Sequential Floating Selection )

　　算法描述：序列浮动选择由增L去R选择算法发展而来，该算法与增L去R选择算法的不同之处在于：序列浮动选择的L与R不是固定的，而是“浮动”的，也就是会变化的。

　　　　序列浮动选择根据搜索方向的不同，有以下两种变种。

　　　　<1>序列浮动前向选择( SFFS , Sequential Floating Forward Selection )

　　　　　　算法描述：从空集开始，每轮在未选择的特征中选择一个子集x，使加入子集x后评价函数达到最优，然后在已选择的特征中选择子集z，使剔除子集z后评价函数达到最优。

　　　　<2>序列浮动后向选择( SFBS , Sequential Floating Backward Selection )

　　　　　　算法描述：与SFFS类似，不同之处在于SFBS是从全集开始，每轮先剔除特征，然后加入特征。

算法评价：序列浮动选择结合了序列前向选择、序列后向选择、增L去R选择的特点，并弥补了它们的缺点。

　　(6) 决策树( Decision Tree Method , DTM)

算法描述：在训练样本集上运行C4.5或其他决策树生成算法，待决策树充分生长后，再在树上运行剪枝算法。则最终决策树各分支处的特征就是选出来的特征子集了。决策树方法一般使用信息增益作为评价函数。

2.2.3 随机算法

　　(1) 随机产生序列选择算法(RGSS, Random Generation plus Sequential Selection)

　　算法描述：随机产生一个特征子集，然后在该子集上执行SFS与SBS算法。

　　算法评价：可作为SFS与SBS的补充，用于跳出局部最优值。

　　(2) 模拟退火算法( SA, Simulated Annealing )

　　　　模拟退火算法可参考大白话解析模拟退火算法。

　　　　算法评价：模拟退火一定程度克服了序列搜索算法容易陷入局部最优值的缺点，但是若最优解的区域太小（如所谓的“高尔夫球洞”地形），则模拟退火难以求解。

　　(3) 遗传算法( GA, Genetic Algorithms )

　　　　遗传算法可参考遗传算法入门。

　　　　算法描述：首先随机产生一批特征子集，并用评价函数给这些特征子集评分，然后通过交叉、突变等操作繁殖出下一代的特征子集，并且评分越高的特征子集被选中参加繁殖的概率越高。这样经过N代的繁殖和优胜劣汰后，种群中就可能产生了评价函数值最高的特征子集。

　　　　随机算法的共同缺点：依赖于随机因素，有实验结果难以重现。

(2)评价函数

(1) 相关性( Correlation)------------filter

运用相关性来度量特征子集的好坏是基于这样一个假设：好的特征子集所包含的特征应该是与分类的相关度较高（相关度高），而特征之间相关度较低的（亢余度低）。

可以使用线性相关系数(correlation coefficient) 来衡量向量之间线性相关度。

　　( 2) 距离 (Distance Metrics )------------filter

运用距离度量进行特征选择是基于这样的假设：好的特征子集应该使得属于同一类的样本距离尽可能小，属于不同类的样本之间的距离尽可能远。

常用的距离度量（相似性度量）包括欧氏距离、标准化欧氏距离、马氏距离等。

　　(3) 信息增益( Information Gain )------------filter

　　假设存在离散变量Y，Y中的取值包括{y₁，y₂，....，y_m} ，y_i出现的概率为Pi。则Y的信息熵定义为：

　　　　信息熵有如下特性：若集合Y的元素分布越“纯”，则其信息熵越小；若Y分布越“紊乱”，则其信息熵越大。在极端的情况下：若Y只能取一个值，即P₁=1，则H(Y)取最小值0；反之若各种取值出现的概率都相等，即都是1/m，则H(Y)取最大值log₂m。

在附加条件另一个变量X，而且知道X=x_i后，Y的条件信息熵(Conditional Entropy)表示为：

　　在加入条件X前后的Y的信息增益定义为

　　　　类似的，分类标记C的信息熵H( C )可表示为：

　　将特征Fj用于分类后的分类C的条件信息熵H( C | Fj )表示为：

　　　　选用特征Fj前后的C的信息熵的变化成为C的信息增益(Information Gain)，用表示，公式为：

　　假设存在特征子集A和特征子集B，分类变量为C，若IG( C|A ) > IG( C|B ) ，则认为选用特征子集A的分类结果比B好，因此倾向于选用特征子集A。

　　(4)一致性( Consistency )-------------filter

若样本1与样本2属于不同的分类，但在特征A、 B上的取值完全一样，那么特征子集{A，B}不应该选作最终的特征集。

　　(5)分类器错误率 (Classifier error rate )---------------wrapper

使用特定的分类器，用给定的特征子集对样本集进行分类，用分类的精度来衡量特征子集的好坏。

　　以上5种度量方法中，相关性、距离、信息增益、一致性属于筛选器，而分类器错误率属于封装器。

(3)停止准则

(4)验证过程

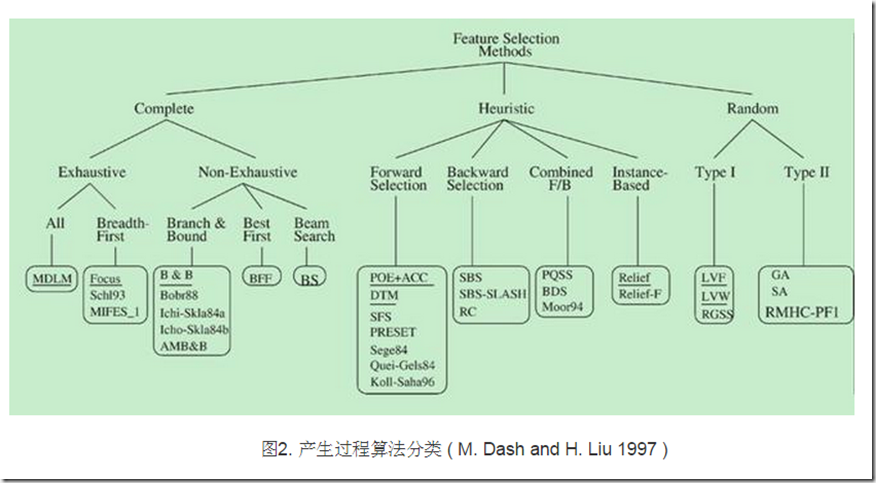
主要分3类:(from wiki)

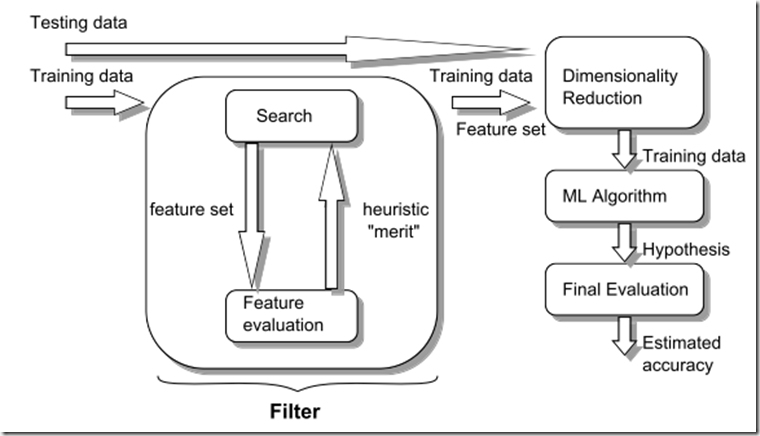
Filter Method

思想:与模型无关.基于一些变特征的衡量标准(即给每一个特征打分,表示这个特征的重要程度),排序后除去那些得分较低的特征..

主要方法:

1.Chi-squared test(卡方检验)

2.information gain(信息增益)或信息增益率

3.correlation coefficient scores(相关系数)

优点:计算时间上较高效,对于过拟合问题具有较高的鲁棒性

缺点:倾向于选择冗余的特征,因为他们不考虑特征之间的相关性,有可能某一个特征的分类能力很差，但是它和某些其它特征组合起来会得到不错的效果

Wrapper Method

思想:根据不同的特征集合所获得的预测效果建立一个黑盒学习,不断优化.

通过目标学习算法来评估特征集合

假如有p个特征，那么就会有2^p种特征组合，每种组合对应了一个模型。Wrapper类方法的思想是枚举出所有可能的情况，从中选取最好的特征组合。

这种方式的问题是：由于每种特征组合都需要训练一次模型，而训练模型的代价实际上是很大的，如果p非常大，那么上述方式显然不具有可操作性。下面介绍两种优化的方法：forward search（前向搜索）和backward search（后向搜索）。

forward search初始时假设已选特征的集合为空集，算法采取贪心的方式逐步扩充该集合，直到该集合的特征数达到一个阈值，该阈值可以预先设定，也可以通过交叉验证获得。算法的伪码如下：

对于算法的外重循环，当F中包含所有特征时或者F中的特征数达到了阈值，则循环结束，算法最后选出在整个搜索过程中最优的特征集合。

backward search初始时假设已选特征集合F为特征的全集，算法每次删除一个特征，直到F的特征数达到指定的阈值或者F被删空。该算法在选择删除哪一个特征时和forward search在选择一个特征加入F时是一样的做法。

将子集的选择看作是一个搜索寻优问题，生成不同的组合，对组合进行评价，再与其他的组合进行比较。这样就将子集的选择看作是一个优化问题，

主要方法:recursive feature elimination algorithm(递归特征消除算法).这里有很多的优化算法可以解决，尤其是一些启发式的优化算法，如GA，PSO，DE，ABC等，详见“优化算法——人工蜂群算法(ABC)”，“优化算法——粒子群算法(PSO)”。

优点:考虑到特征与特征之间的关联性

缺点:1.当观测数据较少时容易过拟合;2.当特征数量较多时,计算时间增长;

Embedded Method(折中)

思想:旨在集合filter和wrapper方法的优点(时间复杂度较低，并且也考虑特征之间的组合关系),在事先了解什么是好的特征的的前提下才可以使用该方法

主要方法:正则化，可以见“简单易学的机器学习算法——岭回归(Ridge Regression)”，岭回归就是在基本线性回归的过程中加入了正则项。我们知道L1正则化自带特征选择的功能，它倾向于留下相关特征而删除无关特征。比如在文本分类中，我们不再需要进行显示的特征选择这一步，而是直接将所有特征扔进带有L1正则化的模型里，由模型的训练过程来进行特征的选择。

优点:集合了前面两种方法的优点

缺点:必须事先知道什么是好的选择

一般来说，特征选择算法的选用需要考虑下因素：
1) 分类器的性能。要显著提高学习算法的性能，可以采用 Wrapper 模型。例如可以选用采用启发式搜索策略的 SBS-SLASH 算法，或基于遗传算法的Wrapper 方法（GA）。

2) 能否去除冗余特征。如果只是要去除不相关的特征，可以采用 Relief 系列算法、互信息法（MI）或 Symmetric Uncertainty，这些算法可以有效的去除和类别不相关的特征，但是无法去除冗余特征。若要同时除去不相关的和冗余特征，可采用 CFS 算法或 FCBF。另外还可以考虑多种算法的结合，例如先用 Relief 算法快速去除不相关的特征，然后采用一种 Wrapper 方法去除冗余特征。
3) 数据集的规模。对于小规模数据，可以采用使用完全搜索策略的 Filter 模型或 Wrapper 模型，例如 BB、BFF、Bobro。对于大规模数据，一般采用运行速度快的 Filter 模型，例如 Relief 系列算法及 FCBF。
4) 类别信息。目前非监督的特征选择算法还比较少，在样本类别未知的情况下，需要选用无监督的特征选择算法，例如 Dash 等提出的一种基于熵的 Filter模型。
5) 数据集的数据类型。Relief 系列算法可以处理数值的（numeric）或名词性的（nominal）属性。互信息（MI）、FCBF 在处理连续的数值属性时，需要预
先对特征离散化。BB、BFF 及 Bobro 等则不能处理名词性的属性

Ref:

Guyon, I., & Elisseeff, A. (2003). An introduction to variable and feature selection. The Journal of Machine Learning Research, 3, 1157-1182.

Hall, M. A. (1999). Correlation-based feature selection for machine learning (Doctoral dissertation, The University of Waikato).(第3\4章)

Kohavi, R., & John, G. H. (1997). Wrappers for feature subset selection.Artificial intelligence, 97(1), 273-324.

M. Dash, H. Liu, Feature Selection for Classification. In:Intelligent Data Analysis 1 (1997) 131–156.

Lei Yu,Huan Liu, Feature Selection for High-Dimensional Data:A Fast Correlation-Based Filter Solution

Ricardo Gutierrez-Osuna, Introduction to Pattern Analysis ( LECTURE 11: Sequential Feature Selection )

http://courses.cs.tamu.edu/rgutier/cpsc689_f08/l11.pdf

http://blog.csdn.net/henryczj/article/details/41043883

http://www.cnblogs.com/heaad/archive/2011/01/02/1924088.html

posted @ 2015-06-09 12:12 max_xbw 阅读(5063) 评论(0) 编辑收藏举报

刷新页面返回顶部

max_xbw