浅谈算法——线段树
前言
线段树作为高级数据结构,可以做非常非常多的事情,那么线段树到底是什么呢,我们就此了解下
一.基本概念
线段树并非什么特别高级的东西,顾名思义,它也就是一棵树。那么为什么叫线段树呢?因为树的节点上存的就是一些区间,也就是线段。那么它长啥样呢?
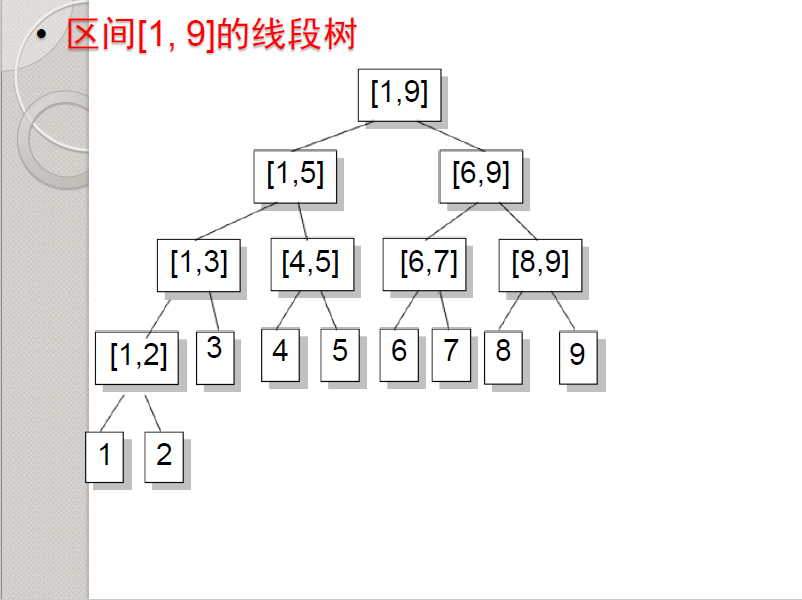
嗯,如上图,就是一个区间[1,9]的线段树。有些节点是叶子节点,叶子节点长度为1,不能继续往下分。叶子节点记录的信息是最基本的信息,而其他非叶子节点记录的就是两个儿子信息的合并(合并的方法有很多,具体情况具体分析)。线段树的左右区间分别为\([l,mid],(mid,r]\)。而且,由于线段树是一颗二叉树,并且线段树是二分构造,所以它非常平衡,深度也是\(log n\)级别的
怎么记录?记录的话,可以学习堆的建造方法,当前点是\(p\),左儿子即是\(p*2\),右儿子就是\(p*2+1\)
二.操作
线段树被发明出来,肯定有它的道理,线段树由于能快速的支持一些操作,因此被广泛使用
1.单点修改
高级数据结构必然要能修改值,修改的话,只需要从线段树的根开始,一路查询到叶子节点,更新完叶子节点后,再将叶子节点到根的路径上的点一路更新一下即可。时间复杂度最大是线段树的深度,即\(O(log n)\)
void change(){//丑陋的伪代码,x是我要修改的点的位置
if (到达叶子节点)
修改当前节点;
return;
}
int mid=区间中点;
if (x<=mid) 对左儿子进行操作;
if (x>mid) 对右儿子进行操作;
更新;
}
2.区间查询
在了解区间查询之前,我们先要知道区间分解
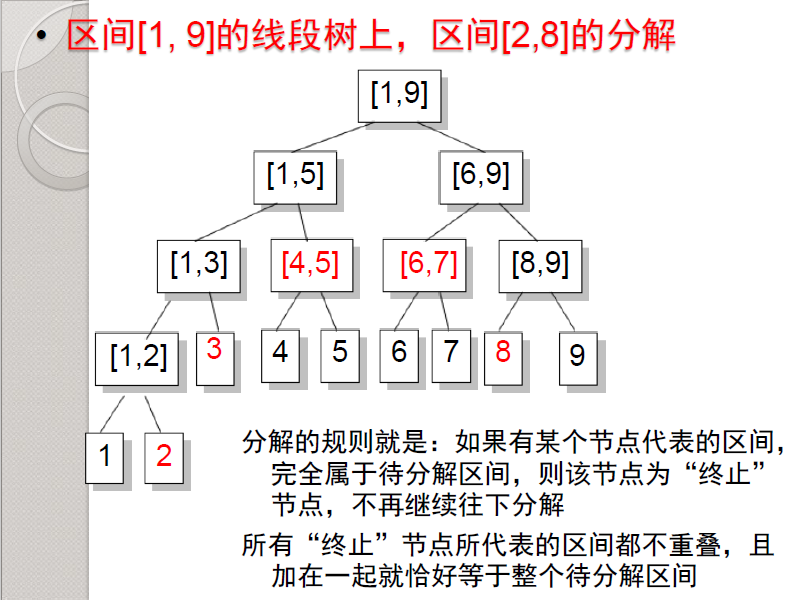
如图就是区间[2,8]的分解,红色的节点表示终止节点。我们只要把所有的终止节点合并起来,就是我所要分解的区间。并且,每层的终止节点一定不会超过2个。所以说,区间查询的时候只需要找到所有的终止节点即可,否则复杂度就上升到\(O(n log n)\),比暴力还差。终止节点每层做多2个,所以查找的复杂度也是\(log n\)量级的
那么如何保证我只找到这些终止区间呢?
int query(){//依然是丑陋的伪代码
//l,r是线段树的区间,x,y是查询区间
if (x<=l&&r<=y) 返回节点信息;//线段树的区间完全包含在查询区间内
int mid=区间中点,ans;
//如果不是完全包含则只需要做两个判断
if (x<=mid) ans=ans+左儿子信息;//查询的区间有部分在左儿子内
if (y>mid) ans=ans+右儿子信息;//查询的区间有部分在右儿子内
return ans;
}
(伪代码实在太丑……下面有一个真正的代码)
三.例题
1.
Description
给定一数列,规定有两种操作,一是修改某个元素,二是求区间的连续和。
Input
输入数据第一行包含两个正整数n,m(n<=100000,m<=500000),以下是m行,
每行有三个正整数k,a,b(k=0或1, a,b<=n).
k=0时表示将a处数字加上b,k=1时表示询问区间[a,b]内所有数的和。
Output
对于每个询问输出对应的答案。
暴力的话,\(O(n^2)\)的复杂度,如果\(n\)到了\(10^6\)的话,这显然是不行的。这个时候,我们就需要用线段树来完成这道题了。单点修改,区间查询,用线段树是很容易实现的
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1e5;
int val[N*4+10];
int read(){
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*f;
}
void change(int p,int l,int r,int x,int t){
if (l==r){
val[p]+=t;
return;
}
int mid=(l+r)>>1;
if (x<=mid) change(p*2,l,mid,x,t);
else change(p*2+1,mid+1,r,x,t);//修改左右儿子,因为建树的原因,所以在x<=mid的时候修改左儿子
val[p]=val[p*2]+val[p*2+1];
}
int get(int p,int l,int r,int x,int y){//对照伪代码即可
if (x<=l&&r<=y) return val[p];
int mid=(l+r)>>1;
int ans=0;
if (x<=mid) ans+=get(p*2,l,mid,x,y);
if (y>mid) ans+=get(p*2+1,mid+1,r,x,y);
return ans;
}
int main(){
int n=read(),m=read();
for (int i=1;i<=m;i++){
int k=read(),x=read(),y=read();
if (!k) change(1,1,n,x,y);
if (k) printf("%d\n",get(1,1,n,x,y));
}
return 0;
}
对于简单的单点修改和区间查询,我们只需要考虑好节点上维护的信息是什么,该怎么修改,询问这些值即可。
2.
Description
给定一行n个正整数a[1]..a[n]。
m次询问,每次询问给定一个区间[L,R],输出a[L]..a[R]的最大公因数。
Input
第一行两个整数n,m。
第二行n个整数表示a[1]..a[n]。
以下m行,每行2个整数表示询问区间的左右端点。
Output
共m行,每行表示一个询问的答案。
这题不牵涉到修改操作,只有查询操作。但是查询是查找\(gcd\)。因此我们对于叶子节点维护点的值,非叶子节点就维护两个儿子节点的\(gcd\)即可
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
int x=0,f=1;char ch=getchar();
for (;ch<'0'||ch>'9';ch=getchar()) if (ch=='-') f=-1;
for (;ch>='0'&&ch<='9';ch=getchar()) x=(x<<1)+(x<<3)+ch-'0';
return x*f;
}
inline void print(int x){
if (x>=10) print(x/10);
putchar(x%10+'0');
}
const int N=1e3,limit=1e9;
int tree[N*4+10];
#define ls (p<<1)
#define rs (p<<1|1)
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
void updata(int p){tree[p]=gcd(tree[ls],tree[rs]);}
void build(int p,int l,int r){
if (l==r){
tree[p]=read();
return;
}
int mid=(l+r)>>1;
build(ls,l,mid),build(rs,mid+1,r);
updata(p);
}
int query(int p,int l,int r,int x,int y){
if (x<=l&&r<=y) return tree[p];
int mid=(l+r)>>1,ans=0;
if (x<=mid) ans=gcd(ans,query(ls,l,mid,x,y));
if (y>mid) ans=gcd(ans,query(rs,mid+1,r,x,y));
return ans;
}
int main(){
int n=read(),m=read();
build(1,1,n);
for (int i=1,x,y;i<=m;i++) x=read(),y=read(),printf("%d\n",query(1,1,n,x,y));
return 0;
}
3.最大连续子数列和
四.尾声
我们讨论了这么多,只是讲了线段树的单点修改和区间查询。那么区间修改该如何解决?请见线段树之Lazy标记



