混沌数学之离散点集图形DEMO
最近看了很多与混沌相关的知识,并写了若干小软件.混沌现象是个有意思的东西,同时混沌也能够生成许多有意思的图形.混沌学的现代研究使人们渐渐明白,十分简单的数学方程完全可以模拟系统如瀑布一样剧烈的行为。输入端微小的差别能够迅速放大到输出端,变成压倒一切的差别,这种现象被称为“对初始条件的敏感性”。
混沌现象其基本含义可以概括为:聚散有法,周行而不殆,回复而不闭。意思是说混沌轨道的运动完全受规律支配,但相空间中轨道运动不会中止,在有限空间中永远运动着,不相交也不闭合。浑沌运动表观上是无序的,产生了类随机性,也称内在随机性。混沌系统具有三个关键要素:一是对初始条件的敏感依赖性;二是临界水平,这里是非线性事件的发生点;三是分形维,它表明有序和无序的统一。混沌系统经常是自反馈系统,出来的东西会回去经过变换再出来,循环往复,没完没了,任何初始值的微小差别都会按指数放大,因此导致系统内在地不可长期预测。
这一节将先展示下混沌点集所生成的图形.这是一个生成混沌离散点集图形的DEMO,里面含有多个不同方程生成的混沌图形.在这个DEMO中,会看到由点集生成的看得出规律的及看不出规律的图形.
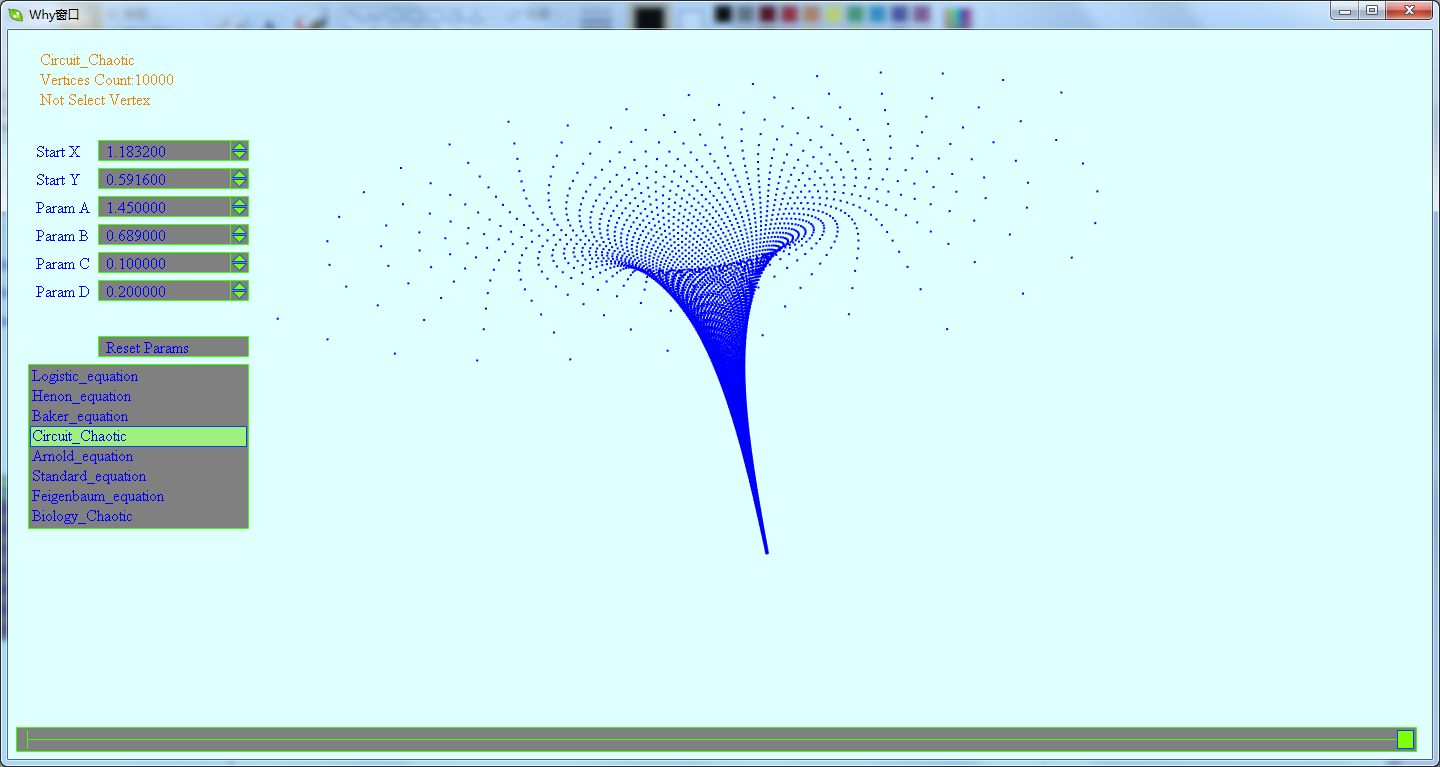
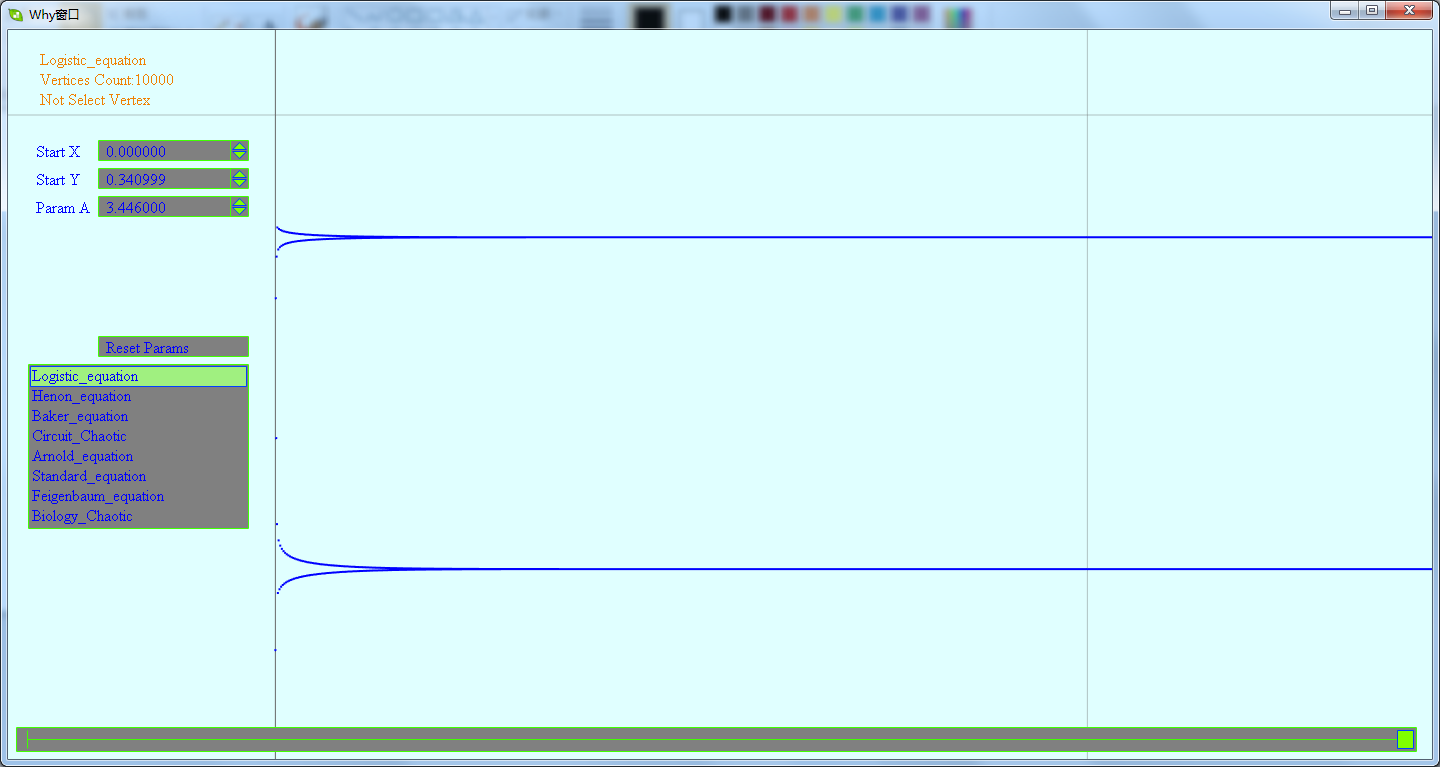
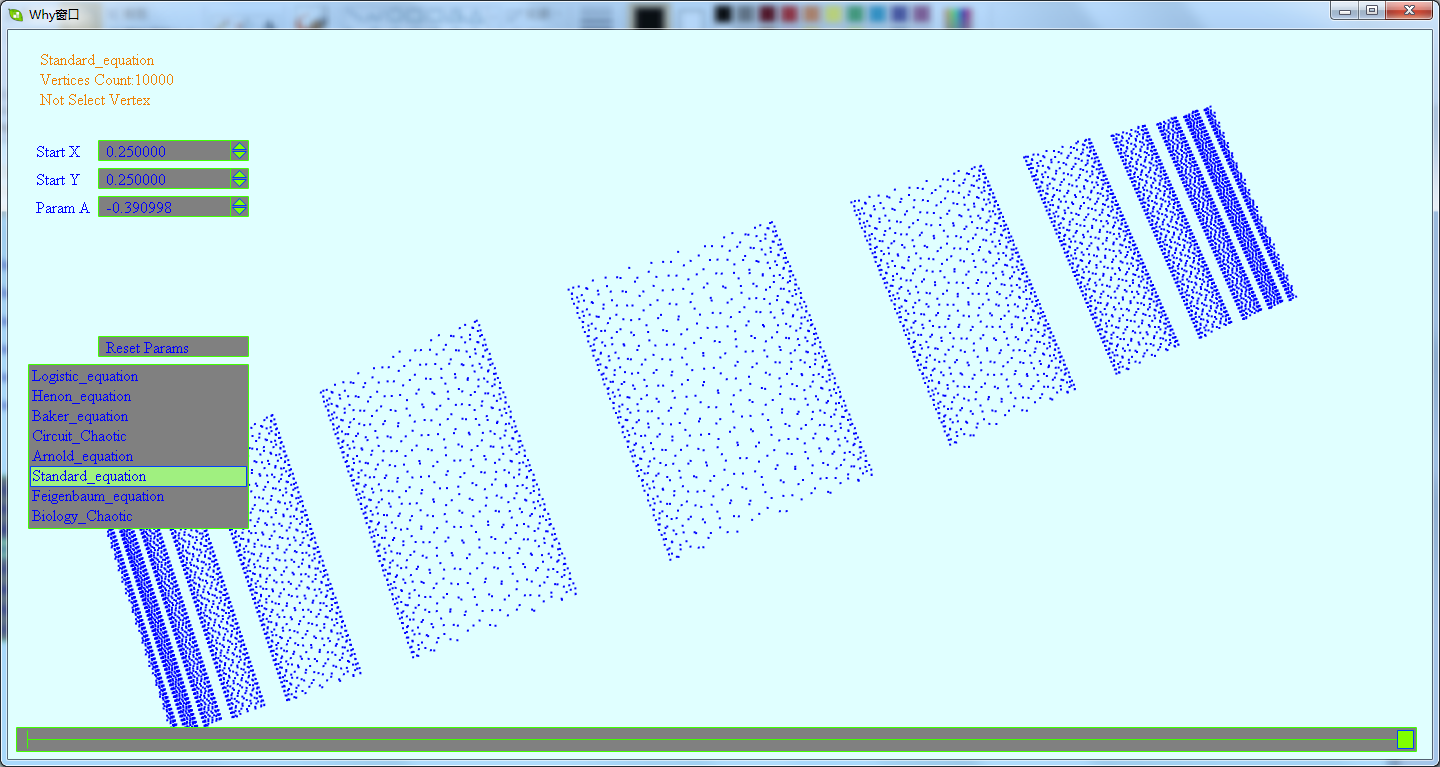
下载地址为:https://files.cnblogs.com/WhyEngine/chaos.7z
软件中有两种视口显示模式,三维和二维的.键盘O用于二者间的切换.
鼠标右键用于控制视口.
键盘G用于是否显示网格的切换
-------------------------------------------------------------
在这种离散点集的混沌图形中,使用迭代的方法生成顶点数据:
在中学课本中我们学过,一个一元函数,通常可以表示为: Y=f(x) 这里X是自变量,Y是因变量。
例如: Y=3X+1,如果X=1,那么Y=4;如果X=4,那么Y=13;总之,如果X被确定,那么相应的Y也被确定。
我们用一个抽象的符号F,来表示Y遵循X变化的因果关系。废话连篇的解释是:数字Y随数字X的变化而变化,Y由X来决定,决定的依据是“关系”F。
如果我们利用某个关系函数,比如Y=F(X),代入一个X算出一个Y,又将Y作为新的X再次计算下一个Y………如此不断,这种方法在数学上称为迭代,具体的表达式是: Xn =F(X n-1 ),n=1,2,3……..
学过程序的人一定知道"费波那齐数列",它算是比较典型的Xn =F(X n-1 )方程的例子。不过这种方程不是收敛的,所以它的图形几下就会爆表。
OK,那先帖下我写的有关这种离散方程对象的基类定义代码:
1 #define SET_GET_FLOAT_PROPERTY(name) \ 2 void Set##name##(float v)\ 3 {\ 4 m_##name## = v;\ 5 }\ 6 float Get##name##() const\ 7 {\ 8 return m_##name##;\ 9 } 10 11 #define PI 3.14159265f 12 13 // -------------------------------------------------------------------------------------- 14 15 class DiscreteEquation 16 { 17 public: 18 DiscreteEquation() 19 { 20 m_StartX = 0.0f; 21 m_StartY = 0.0f; 22 23 m_ParamA = 0.0f; 24 m_ParamB = 0.0f; 25 m_ParamC = 0.0f; 26 m_ParamD = 0.0f; 27 m_ParamE = 0.0f; 28 } 29 30 // 求迭代值 31 virtual void IterateValue(float y, float z, float& outY, float& outZ) const = NULL; 32 33 // 计算点集的Z轴坐标 34 static void CalculatePointsZ(void* curveVerticesPtr, unsigned int stride, unsigned int count, float minZ, float maxZ) 35 { 36 char* zPtr = (char*)curveVerticesPtr + 2*sizeof(float); 37 float zStep = (maxZ - minZ)/(count - 1); 38 39 for (unsigned int i = 0; i < count; i++) 40 { 41 *(float*)zPtr = minZ + i*zStep; 42 zPtr += stride; 43 } 44 } 45 46 // 计算点集的Y轴与X轴坐标 47 virtual void CalculatePointsXY(void* curveVerticesPtr, unsigned int stride, unsigned int count) 48 { 49 char* xPtr = (char*)curveVerticesPtr; 50 char* yPtr = (char*)curveVerticesPtr + sizeof(float); 51 52 float y, x; 53 float nx, ny; 54 55 x = m_StartX; 56 y = m_StartY; 57 58 for (unsigned int i = 0; i < count; i++) 59 { 60 *(float*)xPtr = x; 61 *(float*)yPtr = y; 62 63 IterateValue(x, y, nx, ny); 64 65 x = nx; 66 y = ny; 67 68 xPtr += stride; 69 yPtr += stride; 70 } 71 } 72 73 SET_GET_FLOAT_PROPERTY(StartX); 74 SET_GET_FLOAT_PROPERTY(StartY); 75 76 SET_GET_FLOAT_PROPERTY(ParamA); 77 SET_GET_FLOAT_PROPERTY(ParamB); 78 SET_GET_FLOAT_PROPERTY(ParamC); 79 SET_GET_FLOAT_PROPERTY(ParamD); 80 SET_GET_FLOAT_PROPERTY(ParamE); 81 82 virtual bool IsValidParamA() const {return false;} 83 virtual bool IsValidParamB() const {return false;} 84 virtual bool IsValidParamC() const {return false;} 85 virtual bool IsValidParamD() const {return false;} 86 virtual bool IsValidParamE() const {return false;} 87 88 protected: 89 float m_StartX; 90 float m_StartY; 91 92 float m_ParamA; 93 float m_ParamB; 94 float m_ParamC; 95 float m_ParamD; 96 float m_ParamE; 97 };
每一种混沌点集图形,在程序中都是DiscreteEquation对象的子类.
目前,我已经实现了以下几种混沌方程,将在后来的章节中一一介绍:
(3)混沌数学之Baker模型
(4)混沌数学之CircuitChaotic(二维离散电路混沌系统)
(9)混沌数学之Kent模型
(10)混沌数学之帐篷模型
(11)混沌数学之ASin模型
(12)混沌数学之Henon模型




