数学图形可视化工具的脚本语法
我写了一套数学图形可视化的工具,可以将数学表达式以图形的形式显示出来.
软件下载地址:https://files.cnblogs.com/WhyEngine/WhyMathGraph.zip
源码下载地址: http://pan.baidu.com/s/1jG9QKq6
QQ交流群: 367752815
在这套软件中,我首先制订了一套脚本语言.语法很简单,用于描述数学参数方程,以做为软件的输入数据.
先看下面的脚本程序
Sin曲线
vertices = 1200 x = from (-4*PI) to (4*PI) y = sin(x)

Sin面
vertices = D1:360 D2:100 u = from 0 to 1 D1 v = from -1 to 1 D2 s = 10 x = s*u y = s*v*sin(u*2*PI) u = u*5 v = v*5

(1)顶点数目设置
在计算机图形学中曲线是由顶点组成的
'vertices = 1200' 表示顶点数目,意味着整个曲线上有1200个顶点.
该软件不仅支持曲线还支持曲面,如果是数学曲面图形脚本的话,其顶点输入应该是一个二维的数据.
二维数据用于生成生成曲面图形,其定义如下:
vertices = dimension1:80 dimension2:160 或
vertices = D1:80 D2:160
这里表示第一个维度的输入为80,第二个维度的输入为160,整体输入的顶点数目为80*160.而生成的曲面三角形数目为79*159*2个.
(2)常数值
脚本程序中PI为定义的常数值,就是圆周率,目前软件中有5个常数值
PI 3.1415927
E 2.7182818
GOLD 0.6180034
SQRT2 1.4142136
SQRT3 1.7320508
常量名通常为大写字母,如 (PI + E) 或 sin(PI*0.5)
(3)数值解析
对整数的解析支持2,8,10,16四种进制
0X开头为16进制, XABCDEF大小写都可以, 如0xffff
0Y开头为2进制, Y大小写都可以, 如0y10101010000
0开头为8进制, 如07523, 注意出现了"08"之类的会解析失败
默认为10进制
对浮点数的解析支持两种方式
(a)形如”0.12”的格式,不能省略前面的0,后面也不能加f
(b)科学表达格式.形如1.2e2
(4)变量及其赋值
系统中使用a-z的26个英文小写字母表示变量,变量能够存储单个实数,或一个实数数组.如果为实数数据,则其数组大小为之前设置的顶点数目(见1).
设置为单个实数
a = 3.1415 // 将a赋值为3.1415
a = PI // 将a赋值为常量PI
a = 0y10101010000 //2进制
a = 07523 //8进制
一维数组的设置
a = from 0 to 100 // a为一个实数数组,数组大小为vertices的设置,数值为线性插值求得.得到一个等差数组.
二维数据的设置
a = from 0 to (2*PI) dimension1
b = from (-PI*0.5) to (PI*0.5) dimension2
或者
a = from 0 to (2*PI) D1
b = from (-PI*0.5) to (PI*0.5) D2
这里的D1,D2表示这两个数组是第一维度的数据还是第二个维度的数据.
如果之前设置的vertices = D1:80 D2:160,那么这里a,b所生成的数组大小为80*160
对输出变量的使用:
软件中将变量x,y,z组成3D顶点位置坐标
r,g,b将组成顶点颜色.其值范围在0-1.0之间.如果没有设置r,g,b,将使用默认方式生成顶点色.
u,v为顶点的纹理坐标,如果没有设置u,v,将使用x,z生成顶点的纹理坐标.
(5)运算符
运算符这一块比较多,用户最好看下
”. \MathGraph\Project\MathExpression\operator.cpp”文件中的代码.
以及文件夹” \MathScript\函数面\”里面的脚本文件.
标准单目运算符
+,-
如:a = -b
标准双目运算符
+,-,*,/,%,^ <,>,=,&,|
如:c = a * b 如果a,b都为单个实数则运算结果c也是单个实数,否则c为实数数组.
a^b 等同于pow(a, b)
&|为逻辑运算符,规定当变量-1<a<1时为false,否则为true
函数单目运算符 形如sin(a)
positive,negative,abs,floor,ceil,sign,sqrt,exp,log,log2,log10,sin,cos,tan,asin,acos,atan,rand等
相关代码如下:
const Operator singleOperators[SINGLE_OPERATORS_COUNT] =
{
{"positive", 0, OT_SINGLE, yf_positive, 0, 0, 0, 0, 0},
{"negative", 0, OT_SINGLE, yf_negative, 0, 0, 0, 0, 0},
{"abs", 0, OT_SINGLE, yf_abs, 0, 0, 0, 0, 0},
{"floor", 0, OT_SINGLE, yf_floor, 0, 0, 0, 0, 0},
{"ceil", 0, OT_SINGLE, yf_ceil, 0, 0, 0, 0, 0},
{"sign", 0, OT_SINGLE, yf_sign, 0, 0, 0, 0, 0},
{"rand", 0, OT_SINGLE, yf_rand, 0, 0, 0, 0, 0},
{"rand_int", 0, OT_SINGLE, yf_rand_int, 0, 0, 0, 0, 0},
{"round", 0, OT_SINGLE, yf_round, 0, 0, 0, 0, 0},
{"sqrt", 0, OT_SINGLE, yf_sqrt, 0, 0, 0, 0, 0},
{"exp", 0, OT_SINGLE, yf_exp, 0, 0, 0, 0, 0},
{"log", 0, OT_SINGLE, yf_log, 0, 0, 0, 0, 0},
{"ln", 0, OT_SINGLE, yf_log, 0, 0, 0, 0, 0}, // log == ln
{"log10", 0, OT_SINGLE, yf_log10, 0, 0, 0, 0, 0},
{"lg", 0, OT_SINGLE, yf_log10, 0, 0, 0, 0, 0}, // log10 = lg
{"log2", 0, OT_SINGLE, yf_log2, 0, 0, 0, 0, 0},
{"sin", 0, OT_SINGLE, yf_sin, 0, 0, 0, 0, 0},
{"cos", 0, OT_SINGLE, yf_cos, 0, 0, 0, 0, 0},
{"tan", 0, OT_SINGLE, yf_tan, 0, 0, 0, 0, 0},
{"cot", 0, OT_SINGLE, yf_cot, 0, 0, 0, 0, 0},
{"ctg", 0, OT_SINGLE, yf_cot, 0, 0, 0, 0, 0},
{"asin", 0, OT_SINGLE, yf_asin, 0, 0, 0, 0, 0},
{"acos", 0, OT_SINGLE, yf_acos, 0, 0, 0, 0, 0},
{"atan", 0, OT_SINGLE, yf_atan, 0, 0, 0, 0, 0},
{"acot", 0, OT_SINGLE, yf_acot, 0, 0, 0, 0, 0},
{"arcsin", 0, OT_SINGLE, yf_asin, 0, 0, 0, 0, 0},
{"arccos", 0, OT_SINGLE, yf_acos, 0, 0, 0, 0, 0},
{"arctan", 0, OT_SINGLE, yf_atan, 0, 0, 0, 0, 0},
{"arccot", 0, OT_SINGLE, yf_acot, 0, 0, 0, 0, 0},
{"sinh", 0, OT_SINGLE, yf_sinh, 0, 0, 0, 0, 0}, // 双曲正弦函数
{"cosh", 0, OT_SINGLE, yf_cosh, 0, 0, 0, 0, 0}, // 双曲余弦函数
{"tanh", 0, OT_SINGLE, yf_tanh, 0, 0, 0, 0, 0}, // 双曲正切函数
{"coth", 0, OT_SINGLE, yf_coth, 0, 0, 0, 0, 0}, // 双曲余切函数
{"sh", 0, OT_SINGLE, yf_sh, 0, 0, 0, 0, 0}, // 双曲正弦函数
{"ch", 0, OT_SINGLE, yf_ch, 0, 0, 0, 0, 0}, // 双曲余弦函数
{"th", 0, OT_SINGLE, yf_th, 0, 0, 0, 0, 0}, // 双曲正切函数
{"cth", 0, OT_SINGLE, yf_cth, 0, 0, 0, 0, 0}, // 双曲余切函数
{"sec", 0, OT_SINGLE, yf_sec, 0, 0, 0, 0, 0}, // 正割函数
{"csc", 0, OT_SINGLE, yf_csc, 0, 0, 0, 0, 0}, // 余割函数
{"sech", 0, OT_SINGLE, yf_sech, 0, 0, 0, 0, 0}, // 双曲正割(等同于sch)
{"sch", 0, OT_SINGLE, yf_sech, 0, 0, 0, 0, 0}, // 双曲正割
{"csch", 0, OT_SINGLE, yf_csch, 0, 0, 0, 0, 0}, // 双曲余割(等同于xh)
{"xh", 0, OT_SINGLE, yf_csch, 0, 0, 0, 0, 0}, // 双曲余割
};
函数双目运算符 形如pow(a, b)
add,sub,multiply,divide,max,min,mod,pow,atan2,rand2,等
const Operator twinOperators[TWIN_OPERATORS_COUNT] = { {"add", 0, OT_TWIN, 0, yf_add, 0, 0, 0, 0}, {"sub", 0, OT_TWIN, 0, yf_sub, 0, 0, 0, 0}, {"multiply", 0, OT_TWIN, 0, yf_multiply, 0, 0, 0, 0}, {"divide", 0, OT_TWIN, 0, yf_divide, 0, 0, 0, 0}, {"max", 0, OT_TWIN, 0, yf_max, 0, 0, 0, 0}, {"min", 0, OT_TWIN, 0, yf_min, 0, 0, 0, 0}, {"mod", 0, OT_TWIN, 0, yf_mod, 0, 0, 0, 0}, {"pow", 0, OT_TWIN, 0, yf_pow, 0, 0, 0, 0}, {"log_ax", 0, OT_TWIN, 0, yf_log_ax, 0, 0, 0, 0}, {"pow_sign", 0, OT_TWIN, 0, yf_pow_sign, 0, 0, 0, 0}, {"correction_gamma",0, OT_TWIN, 0, yf_correction_gamma, 0, 0, 0, 0}, {"correction_pow", 0, OT_TWIN, 0, yf_correction_pow, 0, 0, 0, 0}, {"correction_sin", 0, OT_TWIN, 0, yf_correction_sin, 0, 0, 0, 0}, {"atan2", 0, OT_TWIN, 0, yf_atan2, 0, 0, 0, 0}, {"rand2", 0, OT_TWIN, 0, yf_rand2, 0, 0, 0, 0}, {"rand_int2", 0, OT_TWIN, 0, yf_rand_int2, 0, 0, 0, 0}, {"and", 0, OT_TWIN, 0, yf_and, 0, 0, 0, 0}, {"or", 0, OT_TWIN, 0, yf_or, 0, 0, 0, 0}, {"xor", 0, OT_TWIN, 0, yf_xor, 0, 0, 0, 0}, {"greater", 0, OT_TWIN, 0, yf_greater, 0, 0, 0, 0}, {"greater_equal", 0, OT_TWIN, 0, yf_greater_equal,0, 0, 0, 0}, {"less", 0, OT_TWIN, 0, yf_less, 0, 0, 0, 0}, {"less_equal", 0, OT_TWIN, 0, yf_less_equal, 0, 0, 0, 0}, {"equal", 0, OT_TWIN, 0, yf_equal, 0, 0, 0, 0}, };
函数三目运算符 形如lerp(a, b, r)
lerp,clamp,gray,add3,min3,max3,average3
const Operator threeOperators[THREE_OPERATORS_COUNT] = { {"lerp", 0, OT_THREE, 0, 0, yf_lerp, 0, 0, 0}, {"clamp", 0, OT_THREE, 0, 0, yf_clamp, 0, 0, 0}, {"limit", 0, OT_THREE, 0, 0, yf_limit, 0, 0, 0}, {"in_range", 0, OT_THREE, 0, 0, yf_in_range, 0, 0, 0}, {"gray", 0, OT_THREE, 0, 0, yf_gray, 0, 0, 0}, {"add3", 0, OT_THREE, 0, 0, yf_add3, 0, 0, 0}, {"min3", 0, OT_THREE, 0, 0, yf_min3, 0, 0, 0}, {"max3", 0, OT_THREE, 0, 0, yf_max3, 0, 0, 0}, {"average3", 0, OT_THREE, 0, 0, yf_average3, 0, 0, 0}, {"if", 0, OT_THREE, 0, 0, yf_if, 0, 0, 0}, };
比较特殊的是if函数,可以参考这个例子:
vertices = 12000 x = from (-4) to (4) t = mod(x, 2) y = if(t, sin(x*PI), tan(x*PI))
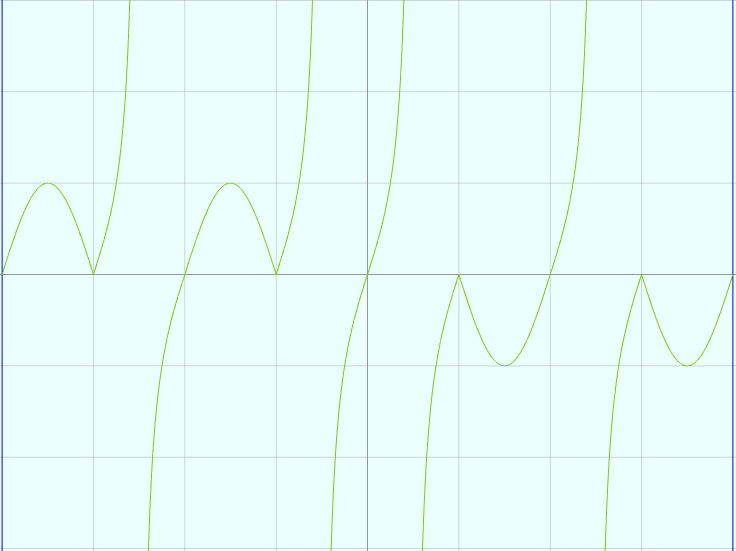
通过if函数,生成一个sin曲线与tan曲线交错的曲线
函数四目运算符 形如average4(a, b, c, d)
add4,min4,max4,average4
const Operator fourOperators[FOUR_OPERATORS_COUNT] = { {"add4", 0, OT_FOUR, 0, 0, 0, yf_add4, 0, 0}, {"min4", 0, OT_FOUR, 0, 0, 0, yf_min4, 0, 0}, {"max4", 0, OT_FOUR, 0, 0, 0, yf_max4, 0, 0}, {"average4", 0, OT_FOUR, 0, 0, 0, yf_average4, 0, 0}, };
函数数组运算符(输入实数数组,输出一个浮点数,如求最大值,最小值,数组加和等)
add_array,min_array,max_array,ave_array
const Operator valueNodeOperators[VALUENODE_TO_FLOAT_OPERATORS_COUNT] = { {"array_add", 0, OT_VALUENODE_TO_FLOAT, 0, 0, 0, 0, yf_add_array, 0}, {"array_min", 0, OT_VALUENODE_TO_FLOAT, 0, 0, 0, 0, yf_min_array, 0}, {"array_max", 0, OT_VALUENODE_TO_FLOAT, 0, 0, 0, 0, yf_max_array, 0}, {"array_ave", 0, OT_VALUENODE_TO_FLOAT, 0, 0, 0, 0, yf_average_array, 0}, };
函数数组运算符(输入实数数组,输出也是实数数组,如求数组左移,数组右移,前向累加等)
array_move_right,array_move_left,array_cumulate
const Operator valueNode2Operators[VALUENODE_CONVERT_OPERATORS_COUNT] = { {"array_move_right",0, OT_VALUENODE_TO_FLOAT, 0, 0, 0, 0, 0, yf_array_move_right}, {"array_move_left", 0, OT_VALUENODE_TO_FLOAT, 0, 0, 0, 0, 0, yf_array_move_left}, {"array_cumulate", 0, OT_VALUENODE_TO_FLOAT, 0, 0, 0, 0, 0, yf_array_cumulate}, };
(6)运算符嵌套
支持{}, [], ()这三类括号标志符,括号必需成对出现.支持最大32级括号的嵌套.如:
(2+(-2+(5.0*(9 + ((1+2)*3))/3) + 2))
-{exp[5*sqrt(1 -abs[sin{rand(100)}]) + 6]}
========================================================
(1)单目运算函数,形如a = log(b)
"positive", // 取正,基本上没什么用,相当于(+a)
"negative", // 取负
"abs", // 求绝对值
"floor", // 整数位
"ceil", // 整数位+1
"sign", // 返回-1.0或1.0
"sgn", // 返回-1.0或0.0或1.0
"is_zero", // 返回0.0或1.0
"rand", // 返回一个随机的浮点数
"rand_int", // 返回一个随机整数
"round", // 四舍五入
"reciprocal", // 倒数
"sqrt", // 开根号
"exp", //
"log", // 求对数
"ln", // log == ln
"log10",
"lg", // log10 = lg
"log2",
"sin", // 正弦函数
"cos", // 余弦函数
"asin", // 反正弦函数
"acos", // 反余弦函数
"arcsin", // 反正弦函数
"arccos", // 反余弦函数
"tan", // 正切函数
"cot", // 余切函数
"ctg", // 余切函数
"atan", // 反正切函数
"acot", // 反余切函数
"actg", // 反余切函数
"arctan", // 反正切函数
"arccot", // 反余切函数
"arcctg", // 反余切函数
"sec", // 正割函数
"csc", // 余割函数
"asec", // 反正割函数
"acsc", // 反余割函数
"arcsec", // 反正割函数
"arccsc", // 反余割函数
"sinh", // 双曲正弦函数
"cosh", // 双曲余弦函数
"tanh", // 双曲正切函数
"coth", // 双曲余切函数
"sh", // 双曲正弦函数
"ch", // 双曲余弦函数
"th", // 双曲正切函数
"cth", // 双曲余切函数
"sech", // 双曲正割(等同于sch)
"sch", // 双曲正割
"csch", // 双曲余割(等同于xh)
"xh", // 双曲余割
"factorial", // 阶乘
"erf", // 误差函数
"float_to_color", // 将浮点数转化为0-255的颜色数
(2)双目运算函数,形如a = add(b, c)
"add", 相加
"sub", 相减
"multiply", 相乘
"divide", 相除
"max", // 返回两数较大的一个
"min", // 返回两数较小的一个
"mod", // 求余
"pow", // 求幂
"log_ax", // 对数
"pow_sign", // 用于对负数的求幂,相当于pow(abs(a), b)
"correction_gamma",// gamma校正函数
"correction_pow", // pow校正函数
"correction_sin", // sin校正函数
"atan2", // 正切
"rand2", // 返回两数之间的一个随机浮点数
"rand_int2", // 返回两数之间的一个随机整数
"and_bool" // 与,返回0或1.0
"or_bool", // 或,返回0或1.0
"xor_bool" // 异或,返回0或1.0
"and_byte" // 与,返回0到255.0的一个数
"or_byte", // 或,返回0到255.0的一个数
"xor_byte" // 异或,返回0到255.0的一个数
"and_word" // 与,返回0到65535.0的一个数
"or_word", // 或,返回0到65535.0的一个数
"xor_word" // 异或,返回0到65535.0的一个数
"greater", // 返回0或1.0
"greater_equal", // 返回0或1.0
"less", // 返回0或1.0
"less_equal", // 返回0或1.0
"equal", // 返回0或1.0
(3)三目运算符函数 形如lerp(a, b, r)
"lerp", // 线性插值
"clamp", // 限定数值的范围
"limit", // 限定数值的范围,与clamp一样
"in_range", // 数值是否范围内,返回0或1.0
"gray", // 颜色的灰度化
"add3", // 相加
"min3", // 三个之中取最小
"max3", // 三个之中取最大
"average3", // 三数平均值
"if", // 如果第一个数不为0则取第二个数,否则取第三个数
"if_else", // 与if等价
(4)函数四目运算符 形如average4(a, b, c, d)
"add4", // 相加
"min4", // 四个之中取最小
"max4", // 四个之中取最大
"average4", // 四数平均值
(5)函数数组运算符(输入实数数组,输出一个浮点数,如求最大值,最小值,数组加和等)
"array_add", // 相加
"array_min", // 数组之中取最小
"array_max", // 数组之中取最大
"array_ave", // 数组平均值
(6)函数数组运算符(输入实数数组,输出也是实数数组,如求数组左移,数组右移,前向累加等)
"array_move_right",// 数组右移
"array_move_left", // 数组左移
"array_cumulate", // 数组累加
"array_difference",// 数组差,b[n] = a[n + params] - a[n]
(7)函数数组运算符(输入两个浮点数,输出实数数组)
"array_lerp", // 将数组中的数值变为等差数列
"array_rand", // 将数组中的数值变为随机浮点数
"array_rand_int", // 将数组中的数值变为随机整数
"array_set_all_values",// 将数组设置为统一值
(8)函数数组运算符(输入实数数组和一个浮点数,输出一个浮点数)
"array_get_value" // 获取数组的某一个值



