2017282110288软件工程第二次作业
一、Github项目地址:
https://github.com/VicLily/softwareEngineering
二、 PSP2.1表格:
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
30 |
60 |
|
· Estimate |
· 估计这个任务需要多少时间 |
30 |
60 |
|
Development |
开发 |
695 |
1130 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
20 |
30 |
|
· Design Spec |
· 生成设计文档 |
60 |
120 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
20 |
20 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
10 |
10 |
|
· Design |
· 具体设计 |
40 |
60 |
|
· Coding |
· 具体编码 |
400 |
700 |
|
· Code Review |
· 代码复审 |
30 |
50 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
120 |
100 |
|
Reporting |
报告 |
80 |
80 |
|
· Test Report |
· 测试报告 |
30 |
20 |
|
· Size Measurement |
· 计算工作量 |
20 |
20 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
30 |
40 |
|
合计 |
|
810 |
1230 |
三、解题思路:
已实现功能:
· 运算符个数、类型、顺序随机生成。
· 操作数随机生成。
· 用户输入题目个数,总分100分,每做完一个题判断对错后输出正确答案。最后给出总分。
· 支持有括号的复合运算(在第二版中,但还存在有bug)
解题思路 :
代码用java实现,另外需要导入JSON的包。
(1)在第一版的代码实现中用了两个集合类(运算符、操作数),所有整数、真分数分子分母分开存储,通过遍历这两个集合类,先计算乘除,后计算加减。
(2)在第二版中用逆波兰算法的思想,这里建立了分子、分母、运算符三个基本栈,然后又建立其他工作栈进行输出和运算操作。
因为刚开始没有想太复杂,所以后来进行了改版,前面的实际时间为第一版的实际时间。
四、设计实现过程:
(1)
第一、首先定义全局变量M用以自定义运算符生成个数的上界,在1-M范围内自动生成操作符的个数num。然后自动生成num+1个操作数,(分子和分母分别自动生成,其中分母不为0,这些数的取值范围也是自定义)。
操作数的映射值是JSONObject类型的,分子和分母以Integer类型存储在里面。
第二、从头遍历一遍运算符的HashMap集合类,遇到乘号或者除号进行相应计算,然后把结果存储到操作数集合DataList里面,遇到加号或者减号则跳过。等到操作符的集合characterList遍历完后乘和除运算已经做完,只剩下加和减操作。重新遍历一遍characterList,计算加减运算。
第三、记两个操作数的分子分母分别为zi1,mu1,zi2,mu2,记两个操作数的计算结果为zi,mu。 操作数的四个值是DataList里两个JSONObject的对象的两个获取值。
当做加运算时:zi1/mu1 + zi2/mu2,分别计算分子和分母,mu=mu1*mu2,zi=zi1*mu2+zi2*mu1。将结果zi,mu约分后存储在DataList
当做减运算时:zi1/mu1 - zi2/mu2,分别计算分子和分母,mu=mu1*mu2,zi=zi1*mu2-zi2*mu1。将结果zi,mu约分后存储在DataList
当做乘运算时:zi1/mu1 * zi2/mu2,分别计算分子和分母,mu=mu1*mu2,zi=zi1*zi2。将结果zi,mu约分后存储在DataList
当做除运算时:zi1/mu1 ÷ zi2/mu2,计算之前先做一个判断,如果除号后面的操作数分子为0,则重新随机生成一个不为0的数。分别计算分子和分母,mu=mu1*zi2,zi=zi1*mu2。将结果zi,mu约分后存储在DataList
第四、在第一次遍历characterList做完乘除操作后,记录下不会再用到的操作符和操作数,然后删除掉,再进行加减操作,加减操作完成后同样删除掉不会再用到的运算符和操作数。最后DataList只剩下最后的结果。将最后结果变成字符串的形式与用户输入的进行比较,如果匹配输出“回答正确”,加上相应的分数。
(2)
在第二版中用逆波兰算法,也是在第一版的基础上做了修改,先建立分子、分母、操作符、括号的集合,随机生成括号对数(1-2对),确定第一个左括号的位置,然后将括号和操作符依次入栈(同一个栈)分子分母分别入栈,然后进行出栈、判断、计算、入栈等一系列操作。最后分子和分母的栈中就是最后的结果,将最后结果变成字符串类型与用户输入的进行比较,判断对错。(第二版中的计算部分与第一版的思想一致,但由于时间关系,目前在判断上还存在bug需要调试修改)
五、代码说明:
(1)第一版:
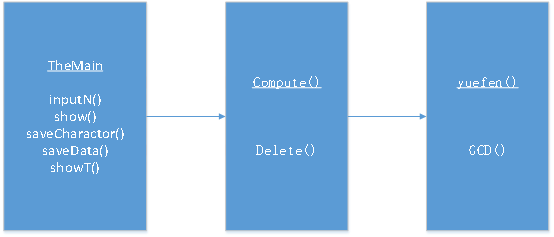
建立了三个.java文件,首先在TheMain类中,有5个内部类,inputN()用来处理用户输入有几个题目,调用show()方法。Show()方法用来显示有满分、每道题目分数、运行saveCharactor()和saveData()方法,循环调用showT()方法和compute()类。
其中saveCharactor()和saveData()方法用来自动生成并存储运算符和操作数。
ShowT()方法用来在控制台输出一个题目给用户。
Compute()类用来计算对应运算符的运算操作,其中用Delete()方法删除计算过不会再使用的运算符和操作数。
Yuefen()类用于对分子和分母的约分,GCD()方法是对分子和分母求最大公约数。
关键代码:
下图中代码是输出除号之前,判断除号后面的操作数是否为0,若为0则重新随机生成一个不为0的真分数存储并输出。

下图代码为随机生成运算符的类型,其中num为自定义操作符个数的全局变量。

(2)第二版:
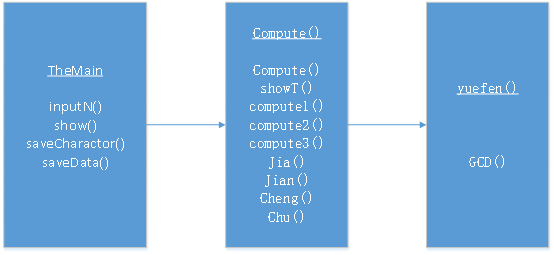
同第一版一样,有三个.java文件。TheMain()类中的方法、yuefen()类与第一版的功能一样。
Compute()类中,compute()方法用来自动生成括号个数以及确定括号的起始位置、调用showT()方法和compute1()方法。
showT()方法用来将自动生成的多项式显示到控制台中,并将集合中的数据和符号入栈。
Compute1()方法用来判断每个出栈的符号,调用compute2对每个符号进行处理。(目前bug主要出现在这个方法里,一些判断还存在问题)。
Compute2()方法用来对加减乘除符号调用对应的jia()、jian()、cheng()、chu()运算操作。
Compute3()用来处理括号里的运算。
jia()、jian()、cheng()、chu()方法和第一版的加减乘除运算的思想一致。
关键代码:
主要为:根据运算符的个数确定括号的对数的范围。如果只有一个运算符,不会生成括号。如果有两个运算符,随机生成0-1对括号。如果有3个以上的运算符,则生成0-2对括号。

六、测试运行:
(1)运行结果:
第一版:
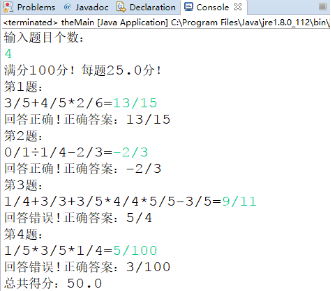
第二版:
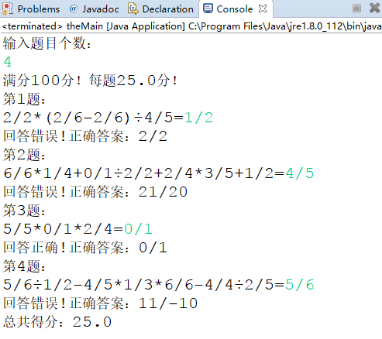
(2)单元测试:
建立一个computeTest的单元测试类,对带括号的compute类进行单元测试,测试代码如下:
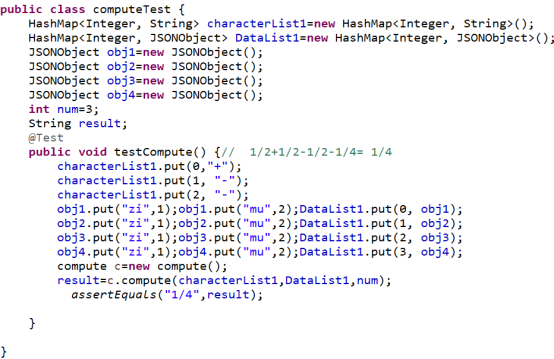
运行过后:由于括号自动生成,所以和手动输入的结果不匹配,导致测试失败。
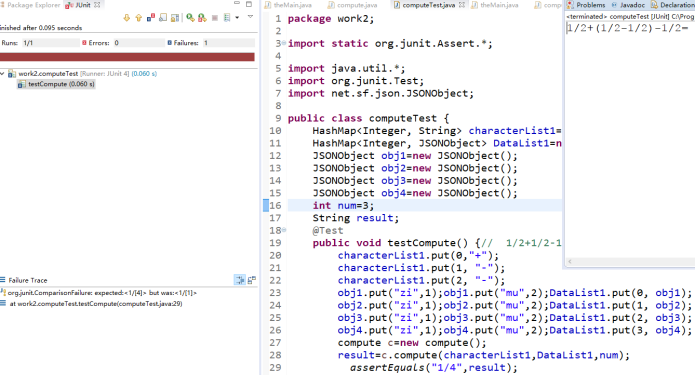
当没有自动生成括号时,运行成功。
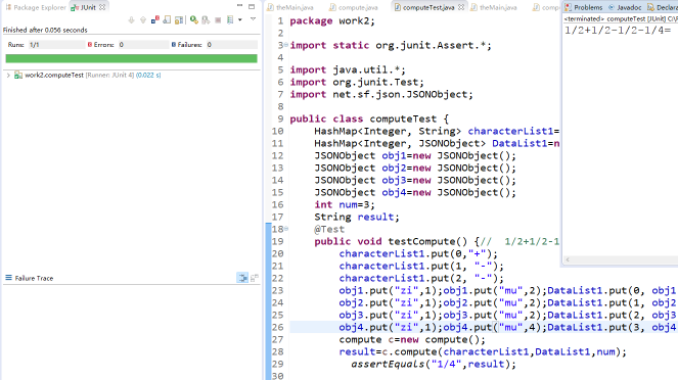
七、项目小结
我先看了《构建之法》的前几章,看题目后感觉并没有那么难,然而在实际做的过程中却遇到了很多问题,我觉得最要紧的就是刚开始构建思路的时候,可能由于经验不足,走了很多弯路,不过结果还算正确运行了出来,等到加括号的运算时候,发现自己之前写的并不是好的代码,不简洁、不清晰,也没有将设计模式运用出来,我觉得可能还需要更多的项目经验来提高编码的能力。





