数值计算（一）

相关概念：

误差：

截断误差：数学模型问题转化为数值问题时，用到离散化、有限展开等方式，导致数值问题与数学模型之间有误差（例如泰勒展开忽略高阶项）

舍入误差：计算机表示浮点数有固定长度，不能准确表达输入数据和输出结果（四舍五入）

向量范数：向量的误差

1-范数：║x║₁=│x1│+│x2│+…+│xn│

2-范数：║x║₂=（│x1│²+│x2│²+…+│xn│²）^1/2

∞-范数：║x║_∞=max（│x1│，│x2│，…，│xn│）

向量误差：若向量x有近似值x₁，应以向量误差为║x-x₁║，相对误差║x-x₁║/║x║

---

线性方程直接解法:没有舍入误差情况下经过有限次运算得到精确解（受限于浮点计算，直接法往往不可能给出解析解）

迭代法：初始向量出发，按照一定计算格式，逐次逼近方程的精确解。只能得到近似解（数值解）

高斯消元：

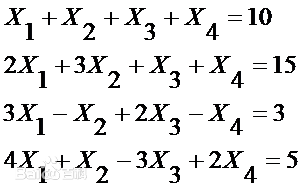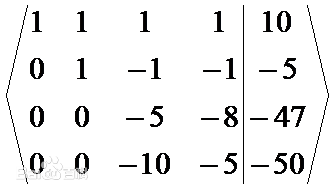例如：   矩阵形式：    消元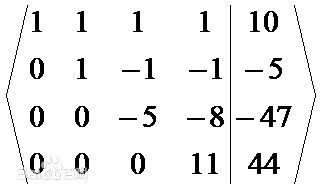：    已知x_{4=44/11=4，回代得到其他未知量，前提对角元素不为0}

LU分解：高斯消元的一个延伸。消元得到上三角矩阵后，以U表示。有A=LU，其中L是一个单位下三角矩阵

---

插值：已知一个函数的数值表（离散的），找一个简单的计算公式，利用它算出给定区间上任意点的值

多项式插值：建立一个n次多项式p(x)，n+1个系数，需要n+1个互异点数据建立方程组，解出系数。

拉格朗日插值多项式：

p(x)=a₀l₀(x)+a₁l₁(x)+...+a_nl_n(x), l_n是n阶函数

例如：当n=4时，上面的公式可简化为：

这是一个过4个点的唯一的三次多项式。

 

牛顿插值多项式：N_n(x)=a₀+a₁(x-x₀)+a₂(x-x₀)(x-x₁)+......+a_n(x-x₀)(x-x₁)(x-n+1)

差商：

 在 的零阶差商为 ；

 

在点

 

与

 

的一阶差商为

  ; 

 

 

在点

 

，

 

，

 

的二阶差商为

  ;

一般的， 在点

  

的k 阶差商为

a₀=f(x₀)=f₀；

a₁=f[x_0,x₁]=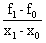

 

a2=f[x0,x1,x2]==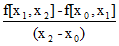

 

---

 

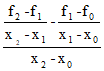
迭代法：

矩阵范数（matrix norm）：

 

1-范数：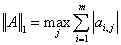

列和范数，即所有矩阵列向量绝对值之和的最大值

2-范数：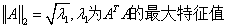

谱范数，即A'A矩阵的最大特征值的开平方

∞-范数：行和范数，即所有矩阵行向量绝对值之和的最大值

F-范数：Frobenius范数，即矩阵元素绝对值的平方和再开平方

条件数：设A为n阶非奇异矩阵（|A|≠0），称数cond(A)=cond(A)=‖A‖·‖A^-1‖ 为方程组Ax=b的条件数或A的条件数。

条件数对A或者b的误差带来的微小扰动起到了放大作用。所以条件数越小，方程组的解得相对误差越小。常用的是cond₂(A)，cond_∞(A) 

基本迭代法：

Ax=b

假设A=M-N

Mx=Nx+b

x=M^-1Nx+M^-1b 

给定一个初始向量x⁽⁰⁾，按照x^(k+1)=M^-1Nx^(k)+M^-1b 或 Mx^(k+1)=Nx^(k)+b迭代至收敛于向量x*，即Ax*=b

可以将A拆成 A=D-L-U

雅克比迭代法： M=D，N=L+U, Dx^(k+1)=(L+U)x^(k)+b

高斯-赛德尔迭代法(GS)：基于雅克比迭代法收敛 Dx^(k+1)=Lx^(k+1)+Ux^(k)+b 或者 (D-L)x^(k+1)=Ux^(k)+b

超松弛（SOR）迭代法： 将高斯-赛德尔迭代法改为x^(k+1)=D^-1（Lx^(k+1)+Ux^(k)+b），可以写成 x^(k+1)=x^(k)+D^-1（Lx^(k+1)+Ux^(k)-Dx^(k)+b）

加一个参数w，  x^(k+1)=x^(k)+wD^-1（Lx^(k+1)+Ux^(k)-Dx^(k)+b）可以获得更快的收敛效果

当w=1， SOR=GS；w>1，收敛速度加快

这三种迭代方法都不能保证收敛性

---

 

收敛性与稳定性

只有既收敛又稳定的方法，才能提供比较可靠的数直结果。显式算法稳定性受时间步长影响，时间步要足够小才稳定（误差积累受到控制），隐式不受时间步长影响，稳定性高于显式，结果更精准，但计算量远大于显格式。在工程项目上说，要确保结果的准确性，或排除问题不出于算法的稳定性，用隐式比较安全。