卷积神经网络cnn的实现

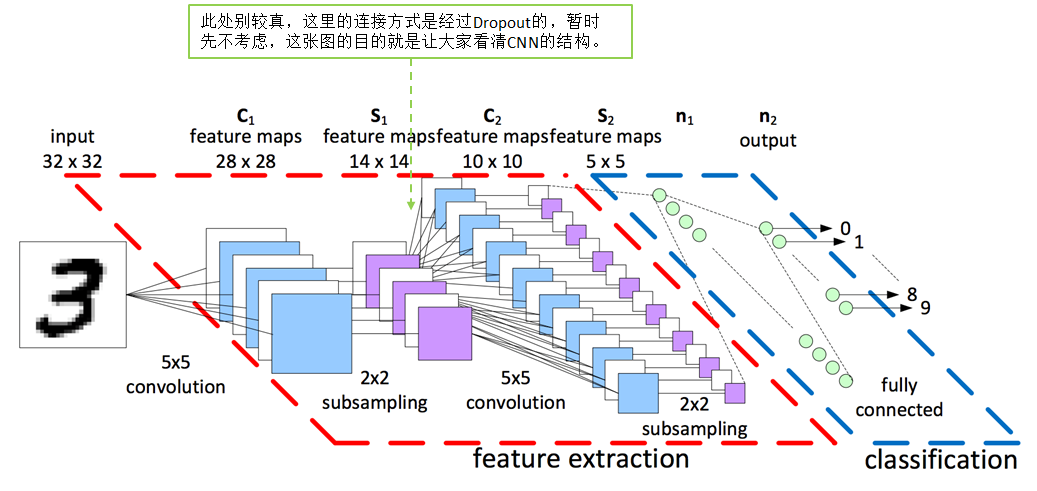
卷积层
原理:基于人脑的图片识别过程,我们可以认为图像的空间联系也是局部的像素联系比较紧密,而较远的像素相关性比较弱,所以每个神经元没有必要对全局图像进行感知,只要对局部进行感知,而在更高层次对局部的信息进行综合操作得出全局信息;即局部感知。
卷积分的知识
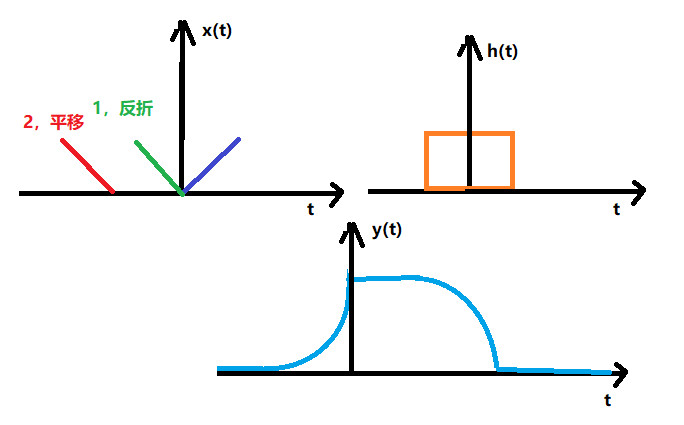
过程:
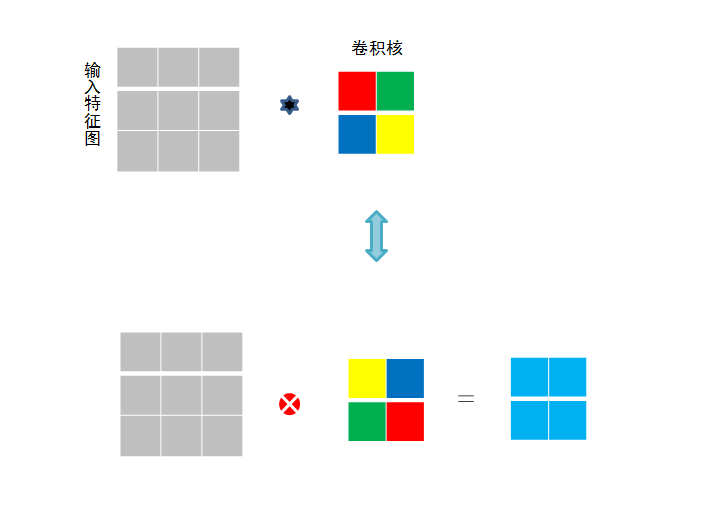
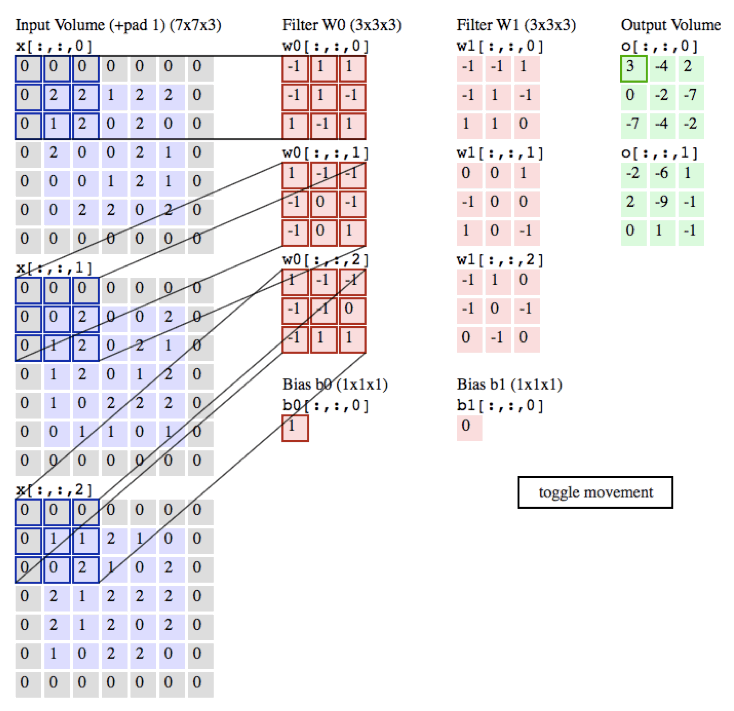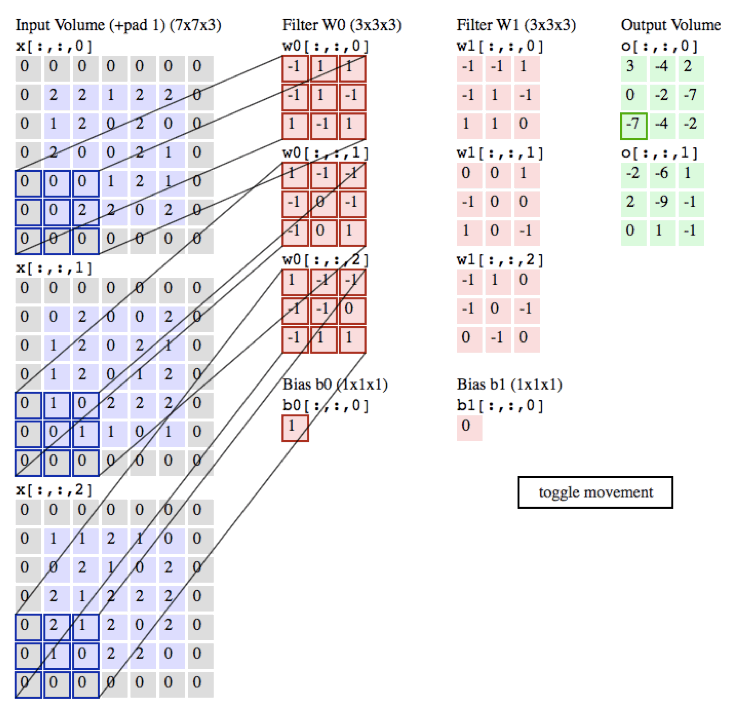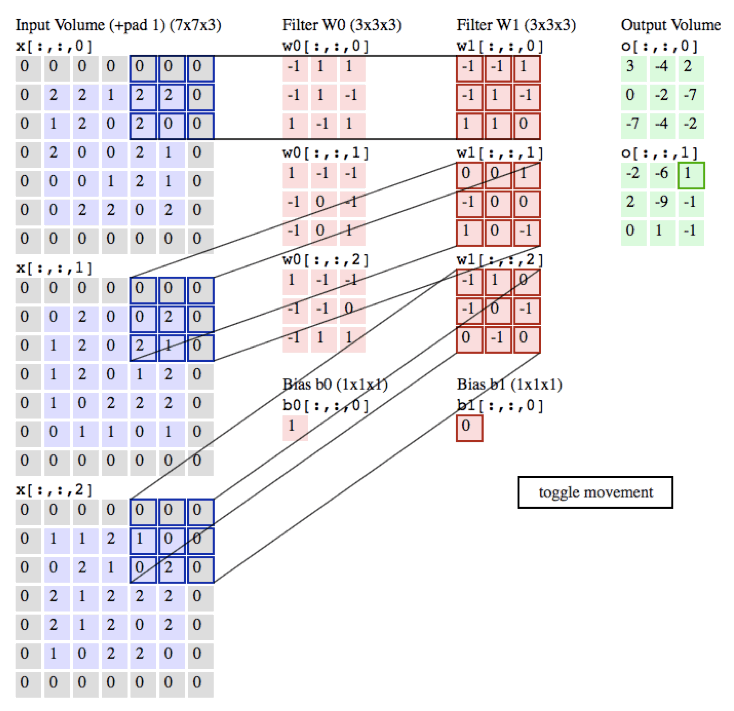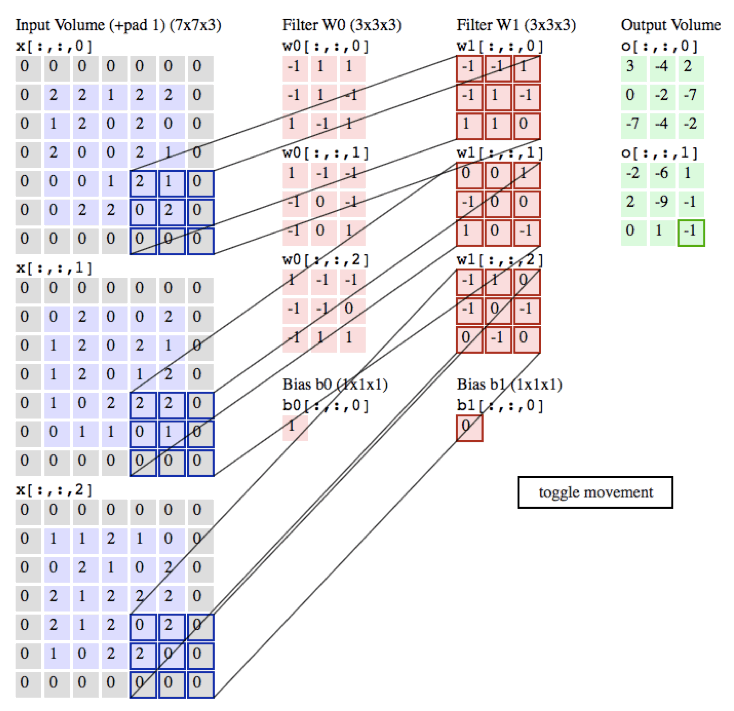
作用:
局部感知:在进行计算的时候,将图片划分为一个个的区域进行计算/考虑; 参数共享机制:假设每个神经元连接数据窗的权重是固定的 滑动窗口重叠:降低窗口与窗口之间的边缘不平滑的特性。
不同的过滤器产生不同的效果:
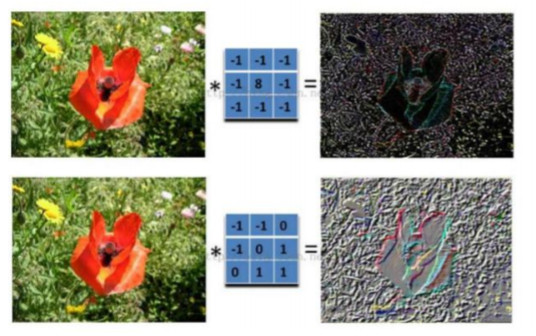
真实做了什么?
一步有一步的浓缩,产生更加靠谱更加准确的特征

一张图片卷积后高和宽如何变化?

# 卷积函数
def conv_fun(cache):
x, w, b = cache["a"], cache["w"], cache["b"]
pad, stride = cache["pad"], cache["stride"]
N, C, H, W = x.shape
F, C, HH, WW = w.shape
# numpy提供的可以填充0的api,constant代表用一样的值填充前两维不填,后两维各自填充pad行
x_padded = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), mode='constant')
H_new = int((H + 2 * pad - HH) / stride) + 1
W_new = int((W + 2 * pad - WW) / stride) + 1
s = stride
out = np.zeros((N, F, H_new, W_new))
for i in range(N): # ith image
for f in range(F): # fth filter
for j in range(H_new):
for k in range(W_new):
out[i, f, j, k] = np.sum
(x_padded[i, :, j * s:(HH + j * s), k * s:(WW + k * s)] * w[f]) +b[f]
return out
池化层
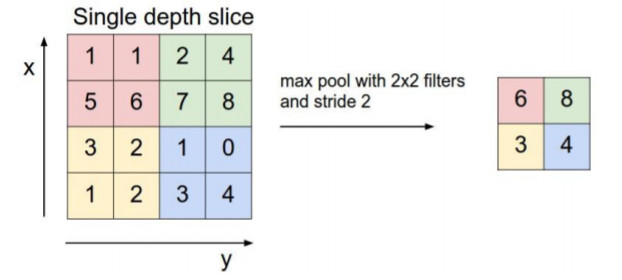
池化层:通过特征后稀疏参数来减少学习的参数,降低网络的复杂度,(最大池化和平均池化)
# 前向池化
def max_pool_forward(cache):
x, HH, WW, s = cache["net"], cache["HH"], cache["WW"], cache["s"]
N, C, H, W = x.shape
H_new = 1 + int((H - HH) / s)
W_new = 1 + int((W - WW) / s)
out = np.zeros((N, C, H_new, W_new))
for i in range(N):
for j in range(C):
for k in range(H_new):
for l in range(W_new):
# 定位到某个窗口
window = x[i, j, k * s:HH + k * s, l * s:WW + l * s]
# 找到该窗口的最大值,然后赋值
out[i, j, k, l] = np.max(window)
return out
ReLU层
http://playground.tensorflow.org/
作用:增加网络非线性的分割能力
# Relu函数
def Relu(x):
return np.maximum(0, x)
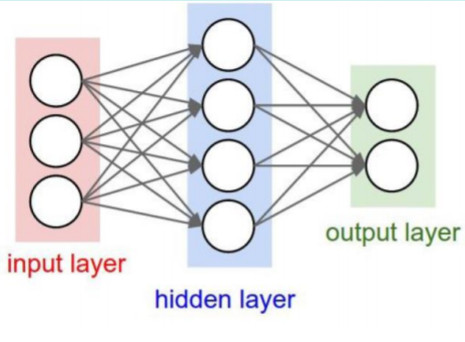
全连接层
# 全连接
def fc(net, w, b):
N = net.shape[0]
# 把每个像素提取出来
x_row = net.reshape(N, -1)
out = np.dot(x_row, w) + b
return out
CNN反向传播的不同之处
首先要注意的是,一般神经网络中每一层输入输出a,z都只是一个向量,而CNN中的a,z是一个三维张量,即由若干个输入的子矩阵组成。其次:
-
池化层没有激活函数。这个问题倒比较好解决,我们可以令池化层的激活函数为σ(z)=z,即激活后就是自己本身。这样池化层激活函数的导数为1。
-
池化层在前向传播的时候,对输入进行了压缩,那么我们向前反向推导上一层的误差时,需要做upsample处理。
-
卷积层是通过张量卷积,或者说若干个矩阵卷积求和而得到当前层的输出,这和一般的网络直接进行矩阵乘法得到当前层的输出不同。这样在卷积层反向传播的时候,上一层误差的递推计算方法肯定有所不同。
-
对于卷积层,由于W使用的运算是卷积,那么由该层误差推导出该层的所有卷积核的W,b的方式也不同。
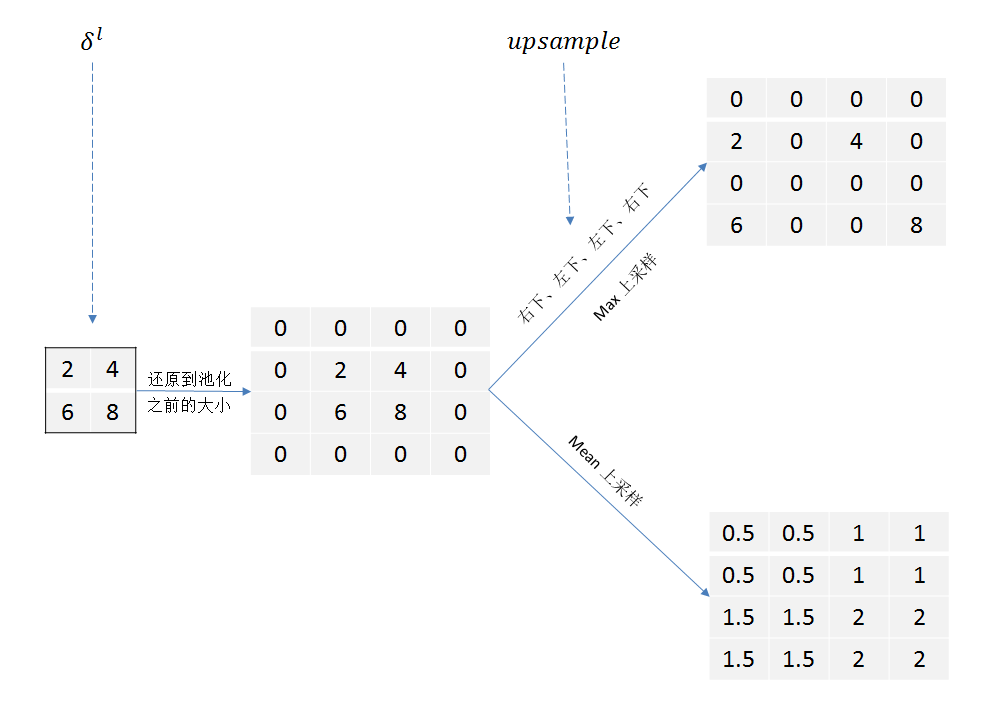
池化层的反向传播
这时候假如前向的时候是最大化池化:

这时候要用到前向传播的时候最大值位置进行还原:

如果是平均:

卷积层的反向传播







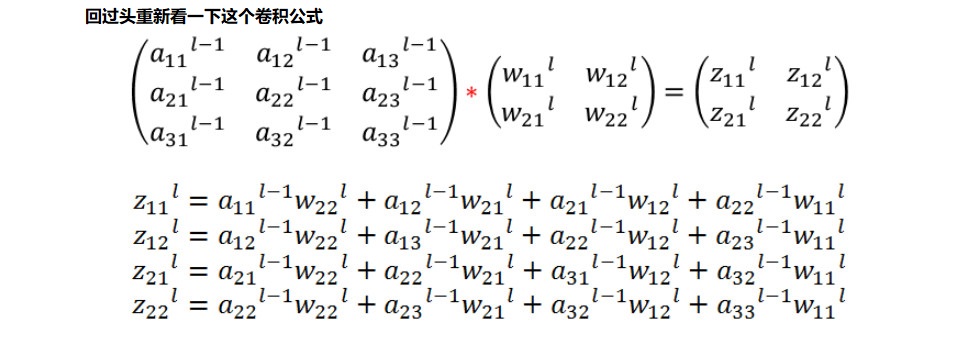

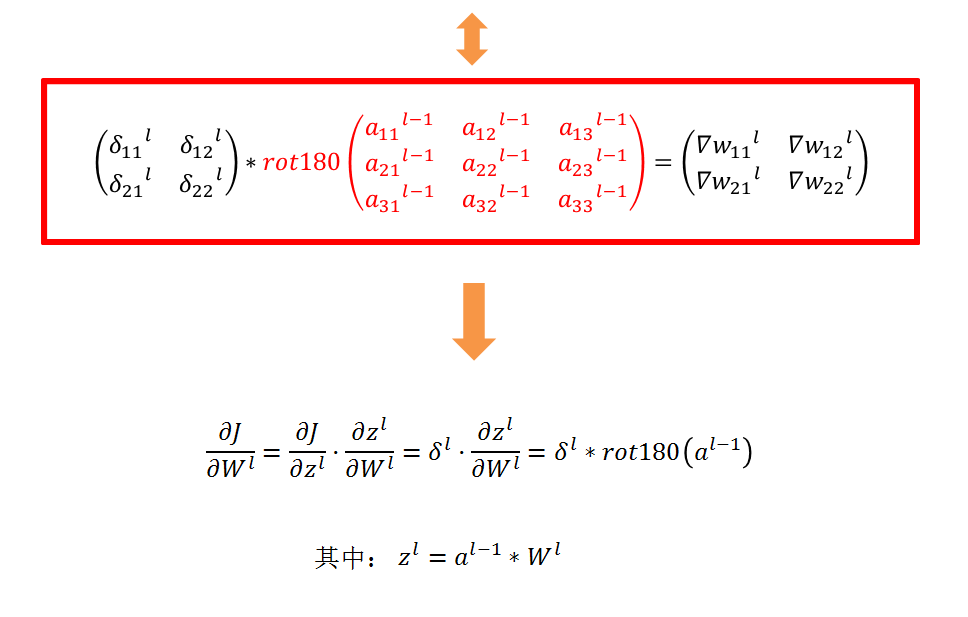
吴恩达笔记中的推导:
卷积神经网络中的反向传播(可选/非梯度)
在现代深度学习框架中,你只需要执行正向传递,这个框架负责向后传递,所以大多数深度学习工程师不会这样做
需要麻烦的细节向后传递。卷积的向后传递网络是复杂的。但是,如果您愿意,您可以完成这个可选部分
来了解卷积网络中的backprop是什么样子的。
在之前的课程中,你实现了一个简单的(完全连接的)神经网络,使用反向传播来计算关于更新成本的导数
参数。类似地,在卷积神经网络中你可以计算为了更新参数对代价求导。backprop方程不是平常那样的,我们在课堂上没有推导出来,但是我们简单地介绍了一下:
Convolutional layer backward pass
让我们从实现CONV层的向后传递开始。
-
计算dA:
这是计算dA对于一定的过滤器Wc的代价的公式以及一个给定的训练例子:
其中Wc是一个过滤器,dZhw是上一层传递过来的梯度,每次我们都将相同的过滤器Wc乘以不同的dZ更新的。我们这样做主要是因为当计算正向传播时,每个过滤器都是由不同的a_slice点乘求和。因此,当计算dA的反向传播的时候,我们也是把所有a_slice的梯度相加。
在代码中,在合适的for循环中,这个公式可以转化为:
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
+=,W[:,:,:,c] * dZ[i, h, w, c]
-
计算dW: 这是计算dWc (dWc是一个过滤器的导数)关于损失的公式:
其中aslice是原样本的一个窗口。因此,这就得到了W关于这个窗口的梯度。这是相同的W,我们将所有这些梯度相加得到dW。
在代码中,在合适的for循环中,这个公式可以转化为:
dW[:,:,:,c] += a_slice * dZ[i, h, w, c] -
计算db: 这是计算db对于一个过滤器Wc的代价的公式:
正如您之前在基本神经网络中看到的,db是通过求和dZ来计算的。在本例中只需对conv输出(Z)的所有梯度求和。
在代码中,在合适的for循环中,这个公式可以转化为:
db[:,:,:,c] += dZ[i, h, w, c]
真实代码:
def conv_backward(dout, cache): x, w, b = cache["a"], cache["w"], cache["b"] pad, stride = cache["pad"], cache["stride"] F, C, HH, WW = w.shape N, C, H, W = x.shape H_new = 1 + int((H + 2 * pad - HH) / stride) W_new = 1 + int((W + 2 * pad - WW) / stride) dx = np.zeros_like(x) dw = np.zeros_like(w) db = np.zeros_like(b) s = stride x_padded = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant') dx_padded = np.pad(dx, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant') for i in range(N): # ith image for f in range(F): # fth filter for j in range(H_new): for k in range(W_new): window = x_padded[i, :, j * s:HH + j * s, k * s:WW + k * s] # db = dout // dw=dout*x // dx = dout*w db[f] += dout[i, f, j, k] dw[f] += window * dout[i, f, j, k] dx_padded[i, :, j * s:HH + j * s, k * s:WW + k * s] += w[f] * dout[i, f, j, k]



