深度学习-卷积神经网络

卷积神经网络CNN

卷积神经网络和普通神经网络非常相似：它们由具有学习权重和偏差的神经元组成。每个神经元接收一些输入，执行点积，并且可选地以非线性跟随它。

整个网络仍然表现出单一的可微分评分功能：

从一端的原始图像像素到另一个类的分数。

并且在最后（完全连接）层上它们仍然具有损失函数，并且我们为学习正常神经网络开发的所有技巧/技巧仍然适用。

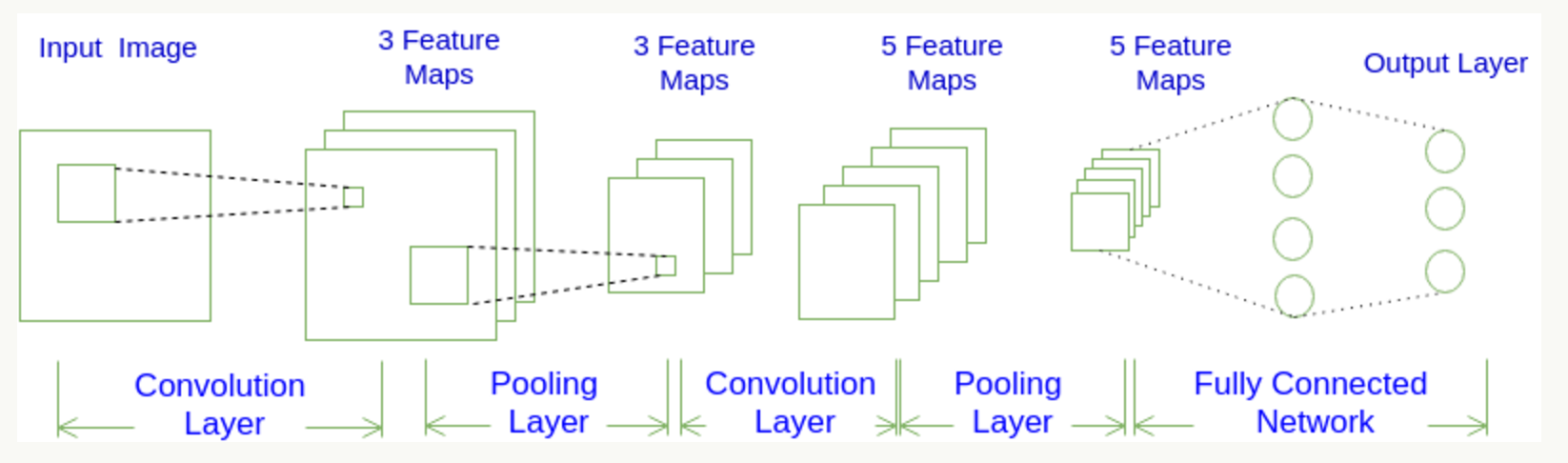
CNN每一层都通过可微分的函数将一个激活的值转换为另一个，一般来说CNN具有卷积层，池化层和完全连接层FC（正如在常规神经网络中所见）,在池化层之前一般会有个激活函数，我们将堆叠这些层，形成一个完整的架构。我们先看下大概的一个图：

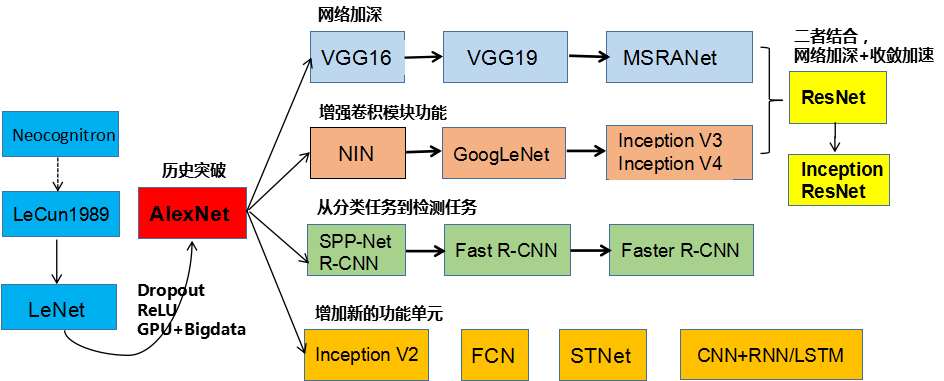
看一下卷积神经网络的发展：

错误率的提升：

卷积网络领域有几种架构，名称。最常见的是：

LeNet。卷积网络的第一个成功应用是由Yann LeCun于1990年代开发的。其中最着名的是LeNet架构，用于读取邮政编码，数字等。
AlexNet。该推广卷积网络计算机视觉中的第一部作品是AlexNet，由亚历克斯·克里维斯基，伊利亚·萨茨基弗和吉奥夫·欣顿发展。AlexNet在2012年被提交给ImageNet ILSVRC挑战，明显优于第二名（与亚军相比，前5名错误为16％，26％的错误）。该网络与LeNet具有非常相似的体系结构，但是更深入，更大和更具特色的卷积层叠在彼此之上（以前通常只有一个CONV层紧随着一个POOL层）。
ZFNet。ILSVRC 2013获奖者是Matthew Zeiler和Rob Fergus的卷积网络。它被称为ZFNet（Zeiler＆Fergus Net的缩写）。通过调整架构超参数，特别是通过扩展中间卷积层的大小，使第一层的步幅和过滤器尺寸更小，这是对AlexNet的改进。
GoogleNet。ILSVRC 2014获奖者是Szegedy等人的卷积网络。来自Google。其主要贡献是开发一个初始模块，大大减少了网络中的参数数量（4M，与AlexNet的60M相比）。此外，本文使用ConvNet顶部的“平均池”而不是“完全连接”层，从而消除了大量似乎并不重要的参数。GoogLeNet还有几个后续版本，最近的是Inception-v4。
VGGNet。2011年ILSVRC的亚军是来自Karen Simonyan和Andrew Zisserman的网络，被称为VGGNet。它的主要贡献在于表明网络的深度是良好性能的关键组成部分。他们最终的最佳网络包含16个CONV / FC层，并且吸引人的是，具有非常均匀的架构，从始至终只能执行3x3卷积和2x2池。他们预先训练的模型可用于Caffe的即插即用。VGGNet的缺点是评估和使用更多的内存和参数（140M）是更昂贵的。这些参数中的大多数都在第一个完全连接的层中，因此发现这些FC层可以在没有性能降级的情况下被去除，
ResNet。Kaiming He等人开发的残留网络是ILSVRC 2015的获胜者。它具有特殊的跳过连接和批量归一化的大量使用。该架构在网络末端也缺少完全连接的层。读者也参考了凯明的演讲（视频，幻灯片），以及一些最近在火炬中复制这些网络的实验。ResNets目前是迄今为止最先进的卷积神经网络模型，并且是实际使用ConvNets的默认选择（截至2016年5月10日）。特别是，也看到最近从Kaiming He等人调整原有架构的发展。

然后介绍一下卷积神经网络的组件:

卷积层：

通过在原始图像上平移来提取特征，每一个特征就是一个特征映射:

就比如黄色的图片就是过滤器,我们利用它去卷积,过程如下:

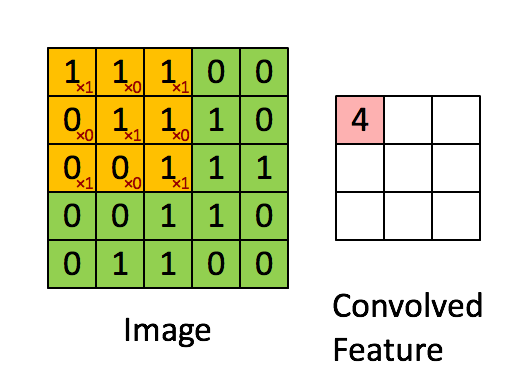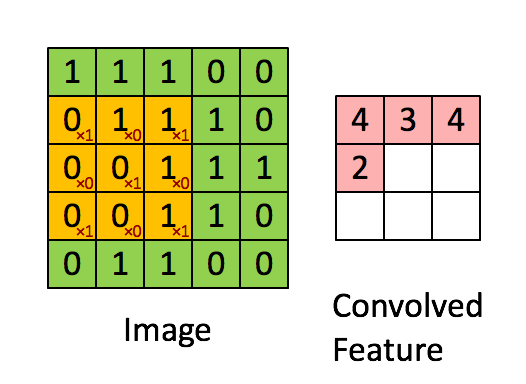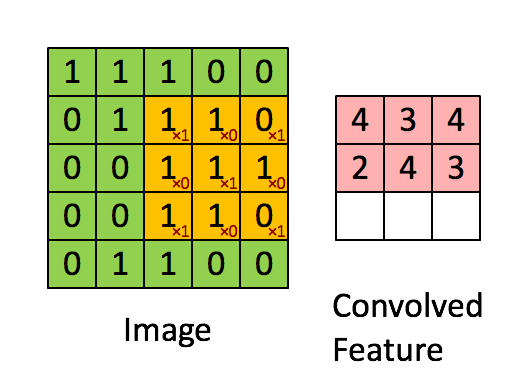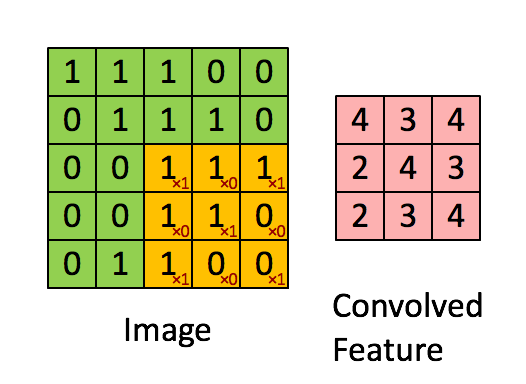
外围补充与多Filter(P)

我们前面还曾提到，每个卷积层可以有多个filter。每个filter和原始图像进行卷积后，都可以得到一个Feature Map。因此，卷积后Feature Map的深度(个数)和卷积层的filter个数是相同的。

如果我们的步长移动与filter的大小不适合，导致不能正好移动到边缘怎么办？

这里就出现了零填充的大小P

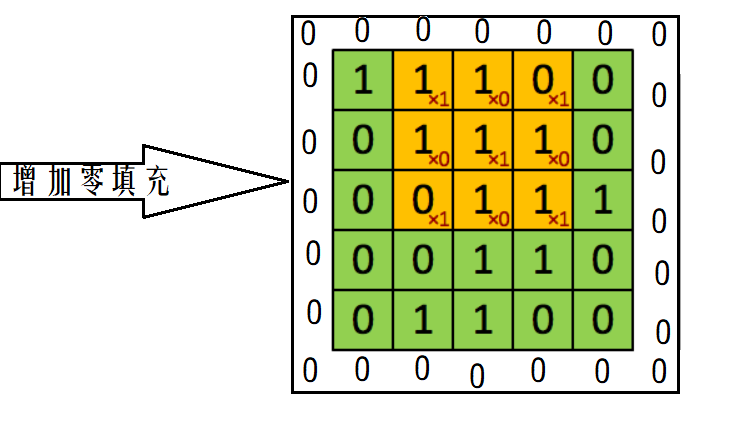
下图就是卷积层的计算方法。这里面体现了局部连接和权值共享：每层神经元只和上一层部分神经元相连(卷积计算规则)，且filter的权值对于上一层所有神经元都是一样的。

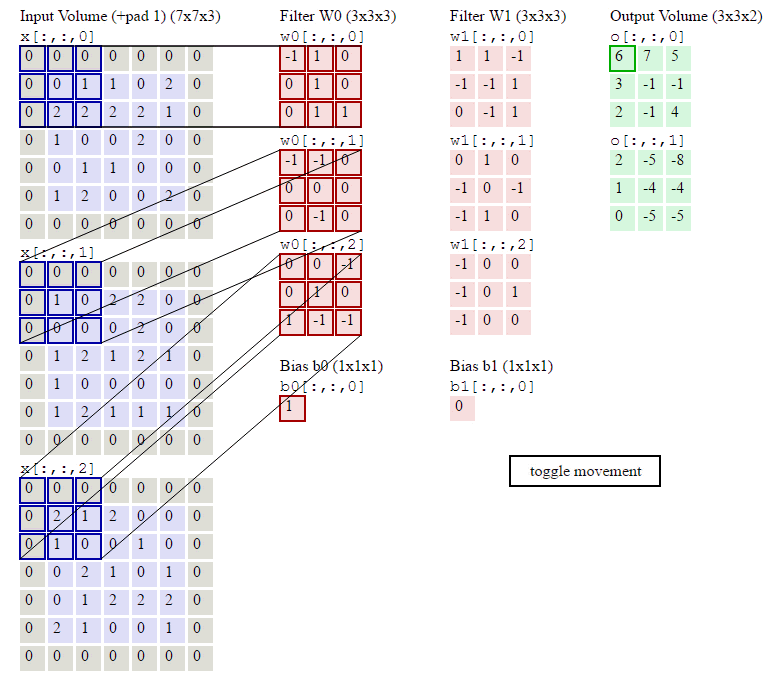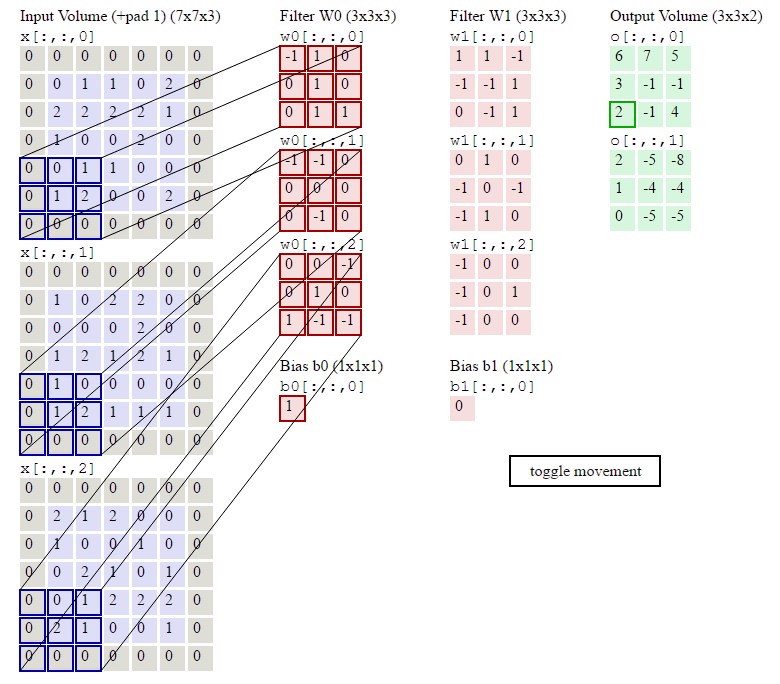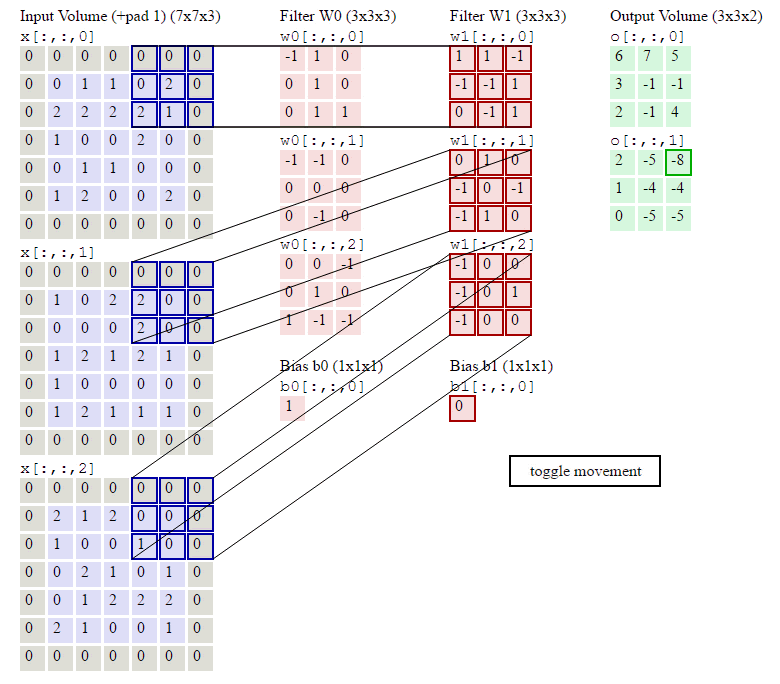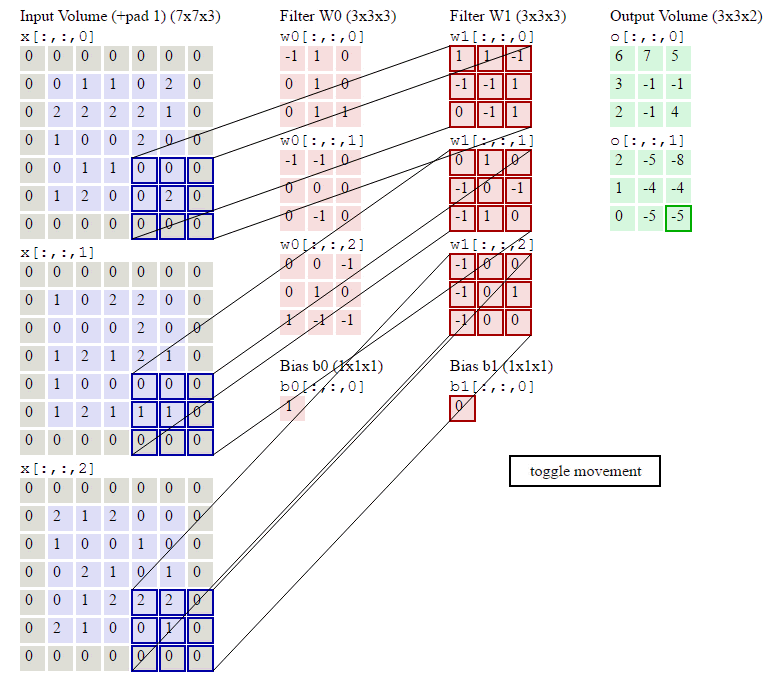
卷积层过滤器:

个数数量K :比如上图就是1个大小大小F: 比如上图就是filter:3*3 步长步长S:比如上图就是1 零填充大小P

•卷积层输出深度、输出宽度

总结输出大小

输入体积大小H1∗W1∗D1
四个超参数：
- Filter数量K
- Filter大小F
- 步长S
- 零填充大小P
输出体积大小H2∗W2∗D2
- H_2 = (H_1 - F + 2P)/S + 1
- W_2 = (W_1 - F + 2P)/S + 1
- D_2 = K

激活函数:

一般在进行卷积之后就会提供给激活函数得到一个输出值。我们不使用sigmoid,softmax，而使用Relu。该激活函数的定义是：

f(x)= max(0,x)

Relu函数如下：

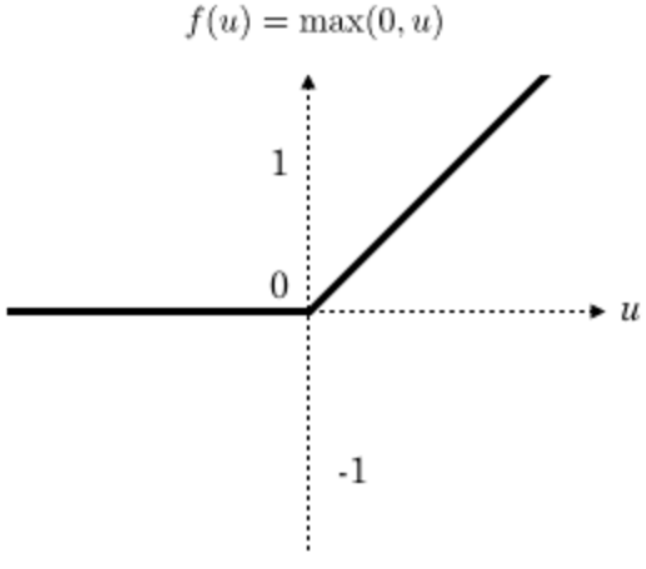
特点

速度快和sigmoid函数需要计算指数和倒数相比，relu函数其实就是一个max(0,x)，计算代价小很多
稀疏性通过对大脑的研究发现，大脑在工作的时候只有大约5%的神经元是激活的，而采用sigmoid激活函数的人工神经网络，其激活率大约是50%。有论文声称人工神经网络在15%-30%的激活率时是比较理想的。因为relu函数在输入小于0时是完全不激活的，因此可以获得一个更低的激活率。

池化层：

通过特征后稀疏参数来减少学习的参数，降低网络的复杂度，（最大池化和平均池化）

Pooling层主要的作用是下采样，通过去掉Feature Map中不重要的样本，进一步减少参数数量。Pooling的方法很多，最常用的是Max Pooling。Max Pooling实际上就是在nn的样本中取最大值，作为采样后的样本值。

除了Max Pooing之外，常用的还有Mean Pooling——取各样本的平均值。对于深度为D的Feature Map，各层独立做Pooling，因此Pooling后的深度仍然为D。

全连接层:

那么在卷积网络当中，为什么需要加上FC层呢？

前面的卷积和池化相当于做特征工程，后面的全连接相当于做特征加权。最后的全连接层在整个卷积神经网络中起到“分类器”的作用

过拟合解决办法

Dropout(失活)

为了减少过拟合，我们在输出层之前加入dropout。我们用一个placeholder来代表一个神经元的输出在dropout中保持不变的概率。这样我们可以在训练过程中启用dropout，在测试过程中关闭dropout。 TensorFlow的tf.nn.dropout操作除了可以屏蔽神经元的输出外，还会自动处理神经元输出值的scale。所以用dropout的时候可以不用考虑scale。一般在全连接层之后进行Dropout

卷积神经网络的构建

一层卷积

卷积：32个filter，5*5，strides 1,padding="SAME"

输入：[None,28,28,1] 输出[None,28,28,32]

激活:[None,28,28,32]

池化:2*2,strides=2,padding="SAME"

输入:[None,28,28,32] 输出:[None,14,14,32]

偏置项:bias = 32

二层卷积

卷积:64个filter,5*5,strides=1,padding="SAME"

输入:[None,14,14,32] 输出[None,14,14,64]

激活:[None,14,14,64]

池化:2*2,strides=2,padding="SAME"

输入:[None,14,14,64] 输出:[None,7,7,64]

偏置项:bias = 64

全连接层FC:

输入:[None,7,7,64]-->[None,7*7*64]

权重:[None,7*7*64,10]

输出:[None,10]

偏置项:bias=10

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

def weight_init(shape):
    w = tf.Variable(tf.random_normal(shape=shape,mean=0.0,stddev=1.0))
    return w
def bias_init(shape):
    b = tf.Variable(tf.constant(0.0,shape=shape))
    return b
def cnn():
    # 1,初始化数据
    mnist = input_data.read_data_sets("data/mnist/input_data/",one_hot=True)
    with tf.variable_scope("data"):
        x = tf.placeholder(tf.float32,[None,784])
        y_true = tf.placeholder(tf.float32,[None,10])
    # 2，第一层卷积 [None,784]-->[None,28,28,1]  5*5*1*32  strides=1-->[None,14,14,32]
    with tf.variable_scope("conv1"):
        x_reshape = tf.reshape(x,[-1,28,28,1])
        w1 = weight_init([5,5,1,32])
        b1 = bias_init([32])
        # 卷积，激活，池化
        x_relu1 = tf.nn.relu(tf.nn.conv2d(x_reshape,filter=w1,strides=[1,1,1,1],padding="SAME")+b1)
        x_poo11 =tf.nn.max_pool(x_relu1,ksize=[1,2,2,1],strides=[1,2,2,1],padding="SAME")
    # 3，第二层卷积 [None,14,14,32]--> 5*5*32*64  strides=1-->[None,7,7,64]
    with tf.variable_scope("conv2"):
        w2 = weight_init([5,5,32,64])
        b2 = bias_init([64])
        # 卷积，激活，池化
        x_relu2 = tf.nn.relu(tf.nn.conv2d(x_poo11,filter=w2,strides=[1,1,1,1],padding="SAME")+b2)
        x_poo12 =tf.nn.max_pool(x_relu2,ksize=[1,2,2,1],strides=[1,2,2,1],padding="SAME")
    # 4，全连接层 [None,7,7,64]->[-1,7*7*64] w [7*7*64,10] b [10]
    with tf.variable_scope("full_connect"):
        w = weight_init([7*7*64,10])
        b = bias_init([10])
        x_fc_reshape = tf.reshape(x_poo12,shape=[-1,7*7*64])
        y_predict = tf.matmul(x_fc_reshape,w)+b
    # 5，损失函数，梯度下降，模型评估
        # 建立损失函数
        with tf.variable_scope("soft_cross"):
            loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_true, logits=y_predict))
        # 梯度下降
        with tf.variable_scope("optimizer"):
            train_op = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
        # 模型评估
        with tf.variable_scope("acc"):
            eq = tf.equal(tf.argmax(y_true, 1), tf.argmax(y_predict, 1))
            accuracy = tf.reduce_mean(tf.cast(eq, tf.float32))
        with tf.Session() as sess:
            tf.global_variables_initializer().run()
            for i in range(1000):
                x_mnist, y_mnist = mnist.train.next_batch(50)
                sess.run([train_op], feed_dict={x: x_mnist, y_true: y_mnist})
                print("训练第%d步,准确率为:%f" % (i, sess.run(accuracy, feed_dict={x: x_mnist, y_true: y_mnist})))
    return None
if __name__ == '__main__':
    cnn()

posted @ 2019-07-26 08:00 Timcode 阅读(548) 评论(0) 编辑收藏举报

刷新页面返回顶部

Timcode