数据结构-栈
一、 栈
- 1. 为什么要学习栈?
栈是什么?为什么要学习它?现在先来说说栈的辉煌作用吧!在计算机领域中,栈是一种不可忽略的概念,无论从它的结构上,还是存储数据方面,它对于学习数据结构的人们来说,都是非常重要的。那么就会有人问,栈究竟有什么作用,让我们这么重视它?首先,栈具有非常强大的“记忆”功能,它可以保存对你有作用的数据,也可以被叫做保存现场;其次,当咱们调用一个带参函数时候, 被调用的函数的形参,在编译器编译的时候,这些形参都需要一定的空间存放他们,这时计算机就会默认帮你保存到栈中了!
- 2. 栈的定义
栈的作用,这是一个咱们生活中处处用到,但是却又没发现的一种现象,例如当你拿个篮子去买苹果,那么你最先挑选的苹果就是在篮子的最底下,最后挑选的苹果就在篮子的最上边,那么这就造成了这么一种现象:先拿进篮子的苹果,要最后才能取出来;相反,最后拿进篮子的苹果,就能最先取出来!
栈是限定只能在表尾进行插入和删除的线性表。
我们把允许插入和删除的一端称作栈顶(Top),另一端称作栈底(bottom)。不含任何数据元素的栈被称作空栈,栈也被称为先进后出的线性表(具有线性关系)。
而栈的特殊性,就是在表中想进行插入和删除的操作,只能在栈顶进行。这也就使得了:栈底是非常稳定的,因为先进来的元素都被放在了栈底。
栈的插入操作:叫做进栈,也叫作压栈,入栈。
栈的删除操作:叫做出栈,也叫弹栈。
- 3. 进栈出栈变化形式
现在请大家思考这样的一个问题:最先进栈的元素,是不是只能最后才能出来呢?
答案是不一定的,这个问题就要细分情况了。栈对线性表的插入和删除的位置进行了限制,并没有对元素的进出时间进行限制,这也就是说,在不是所有元素都进栈的情况下,事先进去的元素也可以先出站,只要确保一点:栈元素是从栈顶出栈就可以了!
举例来说,现在有3个整型数元素1、2、3依次进栈,会有哪些出栈次序呢?
第一种:1、2、3依次进,再3、2、1依次出栈。这是最简单也最好理解的一种,出栈顺序是321。
第二种:1进,1出,2进,2出,3进,3出。也就是进一个出一个,出栈顺序123.
第三种:1进,2进,2出,1出,3进,3出。出栈次序为213。
第四种:1进,1出,2进,3进,3出,2出。出栈次序为132。
第五种:1进,2进,2出,3进,3出,1出。出栈次序为231。
现在思考一下,有没有312这样的出栈次序?
答案是肯定不会的。因为3先出栈,就意味着3曾经进栈,既然3都进栈了,那就意味着1、2已经进栈了,此时,2一定是在1的上面,就是更接近栈顶,那么出栈只能是321,不然不满足123依次进栈的要求,所以此时不会发生1比2先出栈的情况。
上述的这个简单例子,就可以看出来,只是3个栈元素,就有5种可能的出栈次序,如果元素量多,那么出栈的变化将会更多。
二、 栈的抽象数据类型
对于栈来讲,理论上线性表的操作特性它都具备,但是由于它的特殊性,所以针对它的操作上,也会有些变化。特别是插入和删除的操作,我们改名为push和pop,英文翻译为压和弹!
由于栈也是线性表,那么咱们之前讲的线性表的顺序存储和链式存储,对于栈来说,必然也是同样适用的!

一、 ACM算法:顺序栈的实现
既然栈是线性表的特例,那么栈的顺序存储其实也是线性表顺序存储的简化,我们简称为顺序栈。线性表是用数组来实现的,那么对于栈这种只能一头进行插入和删除的线性表来说,咱们一般也是用数组下标为0的一端,作为栈底。
那么此时,我们定义一个StackSize表示数组的元素个数,top变量来指示栈顶元素在数组中的位置,那么就意味着top可以变大变小。如果此栈存在元素,那么top必然要小于StackSize,栈为空则top=-1,栈存在一个元素,top=0。
栈的结构定义:
typedef int SElemType; /* SElemType 类型根据实际情况而定,这里假设为int */
typedef struct
{
SElemType data[MAXSIZE];
int top; /* 栈顶指针 */
}SqStack;
- 1. 栈的顺序存储结构进栈操作
若现在有一个栈,StackSize是5,那么栈的普通情况、空栈、满栈的情况分别如下:

对于栈的插入,即进栈操作,有如下所示:
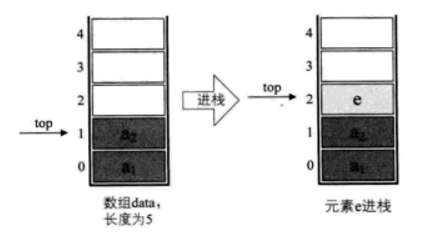
因此对于进栈的操作push,其代码如下:
/* 插入元素e为新的栈顶元素 */ Status Push(SqStack *S,SElemType e) { if(S->top == MAXSIZE -1 ) /* 满栈 */ { return ERROR; } S->top++; /* 栈顶指针增加一 */ S->data[s->top] = e; /* 将新元素e插入并赋值给栈顶空间 */ return OK; }
- 1. 栈的顺序存储结构出栈操作
对于栈的删除,即出栈操作,有如下代码:
/* 先判断栈是否为空,不空则删除S的栈顶元素,用e返回其值,并返回OK,否则返回ERROR */ Statck Pop(SqStack *S, SElemType *e) { if(S->top == -1) return ERROR; *e = S->data[S->top]; /* 将要删除的栈顶元素赋值给e */ S->top-- ; return OK; }
一、 栈的链式存储结构
- 1. 栈出链式存储结构
栈的链式存储结构,简称为链栈。
链栈简单的讲,就是将栈和链表合二为一的使用,那么此时为了简单,通常就把栈顶放在了链表的头指针位置,此时栈顶指针就替代了头指针,那么此时数据依次从栈顶进入,而且此时对于链表来说也就不再需要头结点了。
对于链栈来说,链栈的操作绝大部分都和单链表类似,而且基本上不存在栈满的情况,除非内存已经没有可以使用的空间。
对于空栈来说,链表原定义是头指针指向空,那么链栈的空其实就是top=NULL的时候。
对比一下顺序栈与链栈,它们在时间复杂度上是一样的,均为O(1)。对于空间性能,顺序栈需要事先确定一个固定的长度,可能会存在内存空间浪费的问题,但它的优势是存取时定位很方便,而链栈则要求每个元素都有指针域,这同时也增加了一些内存开销,但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样。如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控的范围内,建议使用顺序栈会更好一些。
栈的链表
/* Note:Your choice is C IDE */ #include "stdio.h" #include "stdlib.h" typedef struct person{ int arr; struct person *next;//入栈压栈push出栈弹栈pop }PERSON; PERSON *head; void main()//栈顶是头指针 { int e; int bh; PERSON *p,*pa,*pb; printf("1.入栈一个元素\n"); printf("2.出栈一个元素\n"); printf("3.打印\n"); for(;;){ printf("请输入功能编号:"); scanf("%d",&bh); switch(bh){ case 1: printf("输入元素:"); scanf("%d",&e); p=(PERSON*)malloc(sizeof(PERSON));//分配一个空间 p->arr=e;//将输入的数据传入链表中 if(head==NULL){ head=p; p->next=NULL; }else{ p->next=head; head=p; } break; case 2: if(head==NULL) { printf("链表为空!\n"); break; } pa=head; pb=head->next; head=head->next; printf("-%d-",pa->arr); free(pa); break; case 3: pa=head; printf("\n打印从栈顶到栈底的元素\n"); while(pa){ printf("--%d--",pa->arr); pa=pa->next; } printf("\n"); break; } } }
栈的顺序表
#include "stdio.h" #define MAX 5 typedef struct person{ int arr[MAX]; int top; }PERSON; PERSON p; void main(void){ int i,e; int bh; p.top=-1; printf("1.入栈一个元素\n"); printf("2.出栈一个元素\n"); printf("3.打印\n"); for(;;){ scanf("%d",&bh); switch(bh){ case 1: if(p.top>=MAX-1){ printf("\n栈已满\n"); }else{ printf("输入元素:"); scanf("%d",&e); p.top++; p.arr[p.top]=e; } break; case 2: e=p.arr[p.top]; printf("删除的元素是%d\n",e); p.top--; break; case 3: printf("\n打印从栈顶到栈底的元素\n"); for(i=p.top;i>=0;i--){ printf("--%d--",p.arr[i]); } printf("\n"); break; } } }



