2-SAT问题的方案输出

2-sat 推荐学习资料：

 

伍昱的2003年IOI国家集训队论文《由对称性解2-sat问题》

 

论文链接：https://wenku.baidu.com/view/31fd7200bed5b9f3f90f1ce2.html

 

注：

本博文只分析如何输出一组可行解，请读者确保已学习了判断是否有解

本人水平不高，若有分析不得当之处，欢迎指出

 

 

法一、tarjan+构建反图+拓扑排序

在原图tarjan缩点后得到的有向无环图的反图上拓扑排序

边拓扑边干两件事儿：

1、选择当前栈顶所代表的问题

2、删除与栈顶问题相对立的问题，删除它在反图上的后继问题

 

个人理解：

 

1、一般情况下，2-SAT的构图是对称的，（原因去看论文）

设i与i'为一对相互对立的问题

若在原图中存在下面的左边的连通子图则必存在右边的连通子图

 

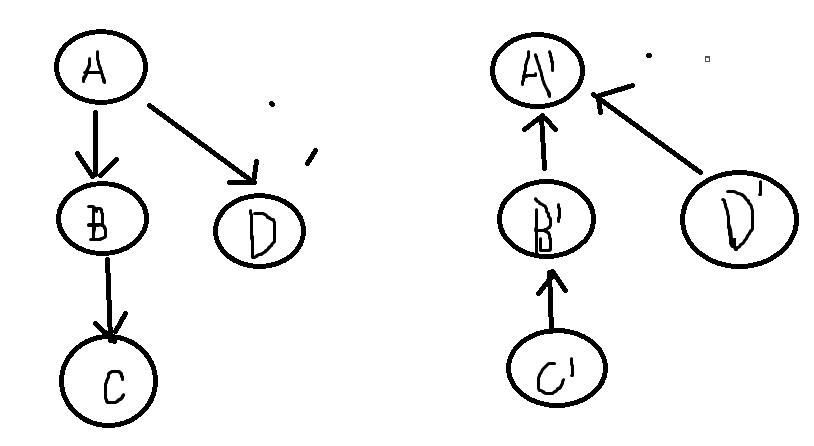
非一般情况比如NOI2017 Day2 T1 游戏，

输入数据会使存在边i-->i'，但不一定存在边i'-->i 

即给出的约束条件使原本就设定的对立问题 再连边

 

2、在原图中一条边u-->v代表着如果选择问题u则必须选择问题v

而选择了问题v不一定要选择问题u

在实现的时候，如果在反图上进行拓扑排序，

反图中入度为0的点，对应着原图中出度为0的点，它在原图中没有后继问题

相当于省去了在原图中拓扑排序的还要选择它所有的后继问题

 

3、在原图中一条边u-->v代表着 如果不选v，则一定不选u

 

栈顶问题的对立问题一定不能选，所以原图中还要删除对立问题的所有前驱问题

 

对应到反图中就是后继问题

在具体实现的时候，我们可以使这些栈顶对立问题的后继问题永远不能入栈

不删除栈顶对立问题的出边即可

 

 

法二：tarjan

tarjan缩点时会给点重新编号

对于一对相互对立的问题，谁的新编号小就选谁

 

此方法对于非对称图也适用

 

反图上在拓扑排序中选择，等价于

原图（缩点后的树）上 从叶子节点开始，自底部向上选择的过程

而tarjan缩点重标号也是从叶子节点往上